What Is Skew Lines In Math
skew lineslineslinesskew lineslinesskew
. In this way, what is skew lines with examples?
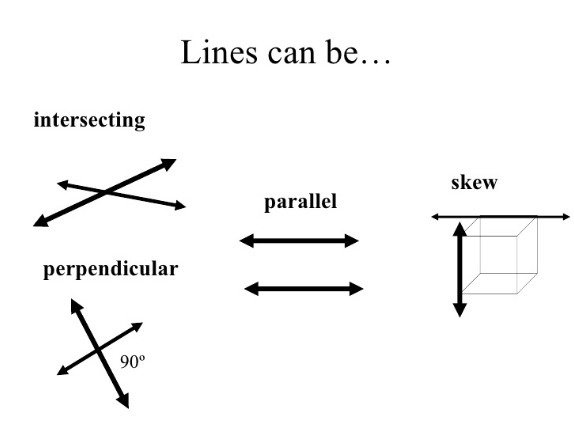
Skew lines are straight lines in a three dimensional form which are not parallel and do not cross. An example of skew lines are the sidewalk in front of a house and a line running across the top edge of a side of a house.
Additionally, how many skew lines does a cube have? 1 Answer. Draw a picture and note that each diagonal has 5 skew lines to make pairs with.
Simply so, what is the difference between parallel and skew lines?
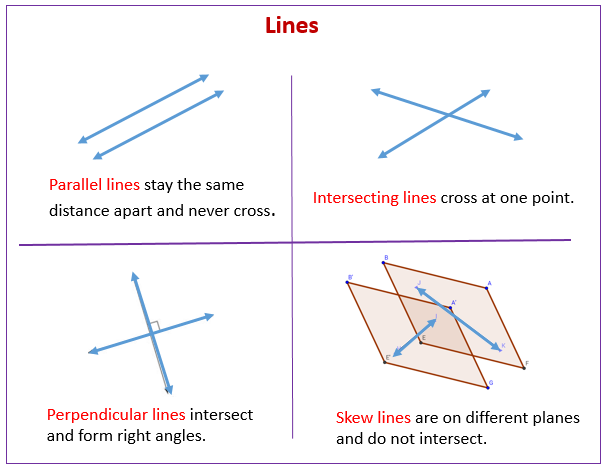
Two or more lines are parallel when they lie in the same plane and never intersect. The difference between parallel lines and skew lines is parallel lines lie in the same plane while skew lines lie in different planes.
Are skew lines perpendicular?
Skew lines are lines that are in different planes and never intersect. A line is said to be perpendicular to another line if the two lines intersect at a right angle. Learn skew line, parallel and perpendicular lines along with skew line exmaples with the help of resources on this page.
Properties Of Skew Symmetric Matrix
- When we add two skew-symmetric matrices then the resultant matrix is also skew-symmetric.
- Scalar product of skew-symmetric matrix is also a skew-symmetric matrix.
- The diagonal of skew symmetric matrix consists of zero elements and therefore the sum of elements in the main diagonals is equal to zero.
- When identity matrix is added to skew symmetric matrix then the resultant matrix is invertible.
- The determinant of skew symmetric matrix is non-negative
The Formulae For Pearsons Skewness Are:
= is the median value \begin & \begin Sk _1 = \frac Mo} \\ \underline \\ Sk _2 = \frac Md} \end\\ & \textbf\\ & Sk_1=\textSk_2\\ & \qquad\ \ \ \text\\ & s=\text\\ & \bar=\text\\ & Mo=\text\\ & Md=\text \end Sk1=sXMoSk2=s3XMdwhere:Sk1=Pearsons first coefficient of skewness and Sk2 the seconds=the standard deviation for the sampleX=is the mean valueMo=the modal valueMd=is the median value
Pearsons first coefficient of skewness is useful if the data exhibit a strong mode. If the data have a weak mode or multiple modes, Pearsons second coefficient may be preferable, as it does not rely on mode as a measure of central tendency.
Dont Miss: Algebra 1 Eoc Fsa Practice Test Calculator Portion
Recommended Reading: Kw Value Chemistry
Applications Of Skewed Data
Skewed data arises quite naturally in various situations. Incomes are skewed to the right because even just a few individuals who earn millions of dollars can greatly affect the mean, and there are no negative incomes. Similarly, data involving the lifetime of a product, such as a brand of light bulb, are skewed to the right. Here the smallest that a lifetime can be is zero, and long lasting light bulbs will impart a positive skewness to the data.
Box Plot And Distributions
In addition to giving you a quick view of the range, the quartiles, and the median, the picture also indicates that if we were to draw a histogram for this data it would look slightly skewed to the left because the box in the box plot is a little towards the left side. In fact, even though the box plot does not directly contain the mean it is possible to estimate whether the mean is less than or greater than the median by looking whether the box plot is skewed to the left or to the right.
First, lets look again at histograms and define what we mean by skewed histograms :
A histogram is called
|
|
|
Most data points fall to the right of the middle, there are more exceptionally large than exceptionally small values. |
Skewed to the left Distribution |
You can tell the shape of the histogram in many cases at least by just looking the box plot, and you can also estimate whether the mean is less than or greater than the median. Recall that the mean is impacted by especially large or small values, even if there are just a few of them, while the median is more stable with respect to exceptional values. Therefore:
As a quick way to remember skewedness:
- longer tail on the left means skewed to the left means mean on the left of median
- longer tail on the right means skewed to the right means mean on the right of median
- tails equally long means normal means mean about equal to median
Distribution is normal, mean and median should be similar
Don’t Miss: Holt Geometry Chapter 7 Test Form A Answers
Eigenvalue Of Skew Symmetric Matrix
If A is a real skew-symmetric matrix then its eigenvalue will be equal to zero. Alternatively, we can say, non-zero eigenvalues of A are non-real.
Every square matrix can be expressed in the form of sum of a symmetric and a skew symmetric matrix, uniquely. Learn various concepts in maths & science by visiting our site BYJUS.
Determinant Of Skew Symmetric Matrix
The determinant of a skew-symmetric matrix having an order equal to an odd number is equal to zero. So, if we see any skew-symmetric matrix whose order is odd, then we can directly write its determinant equal to 0.
Let’s verify this property using a 3×3 matrix as follows:
\(B = \left[\begin0 & a & b \\
Taking conjugate of Ax = x and use the fact that A is real, we have
Ax = \x
-xTAx = -xT\x = -\||x||2.
-\||x||2 = ||x||2
Since x is an eigenvector, it is nonzero by definition. Thus ||x|| 0. Hence we have, -\ = , is either 0 or a purely imaginary number.
Don’t Miss: Geometric Proofs Made Easy
What Is The Sum Of A Symmetric And Skew Symmetric Matrix
We know from the properties of the symmetric and skew symmetric matrices that the sum of any symmetric and a skew symmetric matrix is always a square matrix. Given A is a square matrix then, A = × + × . Here, AT is the transpose of the square matrix A, A + AT is a symmetric matrix, and A – AT is a skew-symmetric matrix.
Title: Configurations Of Skew Lines
Abstract: This paper is an updated version of a survey on projective configurations ofsubspaces in general position. The preceding version was published in Russianin 1989 and in English in 1990 opening a new section“Light reading for the professional”.The paper is written in the form of introduction to the subject, with much ofthe material accessible to advanced high school students. However, in the partof the survey concerning configurations of lines in general position in thethree-dimensional space the exposition is free from any backgroundrestrictions. We have added few new results, fixed few misprints andterminological inaccuracies and expanded the reference list. Notice that someof the results presented in the paper appeared in other papers withoutappropriate references.
Read Also: Figure-ground Psychology
Skew Lines In Geometry
Unlike so many shapes in geometry, skew lines live in our world. They are part of the geometry of three dimensions, just as you and all your friends are three-dimensional beings. Skew lines can only exist in three dimensions they cannot be part of the two-dimensional world of polygons and circles.
Solved Example For You
Question 1: Find the shortest distance between the lines whose equations are:
$$ \vec_1 = \vec + \vec + \lambda $$
$$ \vec_2 = 2 \vec + \vec \vec+ \mu $$
Answer: We shall compare the given equations with the standard form i.e. \vec_1 = \vec_1 + \lambda \vec_1 and vec_2 = \vec_2 + \mu \vec_2. Accordingly, we have:
$$ a_1 = \vec + \vec , b_1 = 2 \vec \vec + \vec $$
$$ a_2 = 2 \vec + \vec \vec , b_2 = 3\vec 5 \vec + 2 \vec $$
So, we can find the shortest distance as :
$$ d = | . | / | \times | $$
= | 3 0 + 7 | / 1/2
= |10| / 1/2 is the shortest distance between the given lines.
Question 2: How does the skew lines look like?
Answer: The skew lines are those lines which do not intersect, but also never lie on a similar plane. They look like they are running in similar directions and even look totally random.
Question 3: Can skew lines be perpendicular?
Answer: A line is said to be perpendicular to the other line only if they are intersecting at a right angle, and we know that the skew lines never intersect or meet, so, the skew lines can never become a perpendicular.
Question 4: What are the dissimilarities between the parallel lines and the skew lines?
Answer: The most common difference between the parallel lines and the skew lines is that the parallel lines lie in a similar plane whereas the skew lines lie in dissimilar planes.
Question 5: How can we prove the skew lines?
Read Also: Chapter 10 Test Form 2a Geometry Answers
Distance Between Skew Lines Formula
To find the distance between the two skew lines, we have to draw a line that is perpendicular to these two lines. We can represent these lines in the cartesian and vector form to get different forms of the formula for the shortest distance between two chosen skew lines.
Say we have two skew lines P1 and P2. We will study the methods to find the distance between two skew lines in the next section.
Examples Of Skew Lines
The edges of the pyramid above form skew lines. Each of the four faces of the pyramid define a unique plane . Line segments AB, AC, and BC, for instance, define a unique plane, and each plane constitutes one of the four faces of the pyramid. None of the three line segments can be skew lines relative to one another because they all lie in the same plane. Recall that lines in the same plane either intersect or are parallel to one another.
There are, however, several pairs of line segments on the pyramid that form skew lines. Line segments AB and CD form a pair of such lines. These two segments are skew to one another because they are neither parallel nor intersecting. Even if the line segments are extended into infinite lines, they still remain skew. Though some of the line segments are hidden from view in this picture, one can envision several other pairs of skew lines formed by the edges of the pyramid.
A cube possesses many combinations of parallel, perpendicular, and skew line segments. The cubes above illustrate different line pairs: parallel, perpendicular, and skew. The shortest distance between the two skew lines is the length of the dashed line segment, which is perpendicular to both of the indicated skew lines. Any other distance measured between the two skew lines will be longer than the dashed line segment.
see also Lines, Parallel and Perpendicular.
Philip Edward Koth (with
You May Like: Chapter 9 Test Form 2a
Asset Prices As Examples Of A Skewed Distribution
The departure from “normal” returns has been observed with more frequency in the last two decades, beginning with the internet bubble of the late 1990s. In fact, asset returns tend to be increasingly right-skewed. This volatility occurred with notable events, such as the Sept. 11 terrorist attacks, the housing bubble collapse and subsequent financial crisis, and during the years of quantitative easing .
The unwinding of the Federal Reserve Board’s unprecedented easy monetary policy may be the next chapter of volatile market action and more asymmetrical distribution of investment returns. Most recently we saw extreme downside moves during the beginning of the global COVID-19 pandemic.
Example : Size Of Rat Litters
For a second illustration of inferences about skewness andkurtosis of a population, Ill use an example fromBulmer :
| Frequency distribution of litter size inrats, n=815 | |
|---|---|
| Litter size | |
| 25 | 4 |
Ill spare you the detailed calculations, but youshould be able to verify them by following equation and equation :
n = 815, x = 6.1252, m2 = 5.1721,m3 = 2.0316
skewness g1 = 0.1727 and sample skewness G1 =0.1730
The sample is roughly symmetric but slightly skewed right, which looksabout right from the histogram. Thestandard error of skewness is
SES = / = 0.0856
Dividing the skewness by the SES, you get the test statistic
Zg1 = 0.1730 / 0.0856 = 2.02
Since this is greater than 2, you can say thatthere is some positive skewness in the population.Again, some positive skewness just means afigure greater than zero it doesnt tell us anything more aboutthe magnitude of the skewness.
If you go on to compute a 95% confidence interval of skewnessfrom equation , you get 0.1730±2×0.0856 = 0.00 to0.34.
What about the kurtosis?You should be able to follow equation and compute a fourth momentof m4 = 67.3948. You already havem2 = 5.1721, and therefore
kurtosis a4 = m4 / m2² = 67.3948 / 5.1721² =2.5194
excess kurtosis g2 = 2.51943 = 0.4806
sample excess kurtosis G2 = [816× = 0.4762
So the sample is moderately less peaked than a normaldistribution. Again, this matches the histogram, where you can seethe higher shoulders.
SEK = 2 × SES × / )
Recommended Reading: Geometry Basics Homework 2 Segment Addition Postulate
What Are Skew Lines
Skew lines are lines that are in different planes, they are never parallel, and they never intersect. On the other hand, parallel lines are lines that are in the same plane and never intersect.
In other words, Parallel lines must exist in two dimensions they are parallel within the same plane. Skew lines cannot exist in two dimensions and are always in different, non-intersecting planes.
Suppose you wanted to build a big wooden box to hold line segments. You would find the longest line segment and make the box slightly bigger than that, right? What if, though, you wanted to hold rays, or lines? No box exists that could hold either, because rays continue in one direction forever, and lines continue in two directions forever.
Skew lines are what you would have if you tried to store lines in a big box. Like a bunch of infinite, double-ended arrows, they would not cooperate.
Skew lines have several identifying properties that make the big wooden box impractical:
- They continue in two directions forever
- They are in different planes
- They are never parallel
- They never intersect
Skew Flats In Higher Dimensions
In higher-dimensional space, a flat of dimension k is referred to as a k-flat. Thus, a line may also be called a 1-flat.
Generalizing the concept of skew lines to d-dimensional space, an i-flat and a j-flat may be skew if i + j< d. As with lines in 3-space, skew flats are those that are neither parallel nor intersect.
In affine d-space, two flats of any dimension may be parallel.However, in projective space, parallelism does not exist two flats must either intersect or be skew.Let I be the set of points on an i-flat, and let J be the set of points on a j-flat.In projective d-space, if i + j d then the intersection of I and J must contain a -flat.
In either geometry, if I and J intersect at a k-flat, for k 0, then the points of I J determine a -flat.
Recommended Reading: What Are Two Types Of Elastic Forces
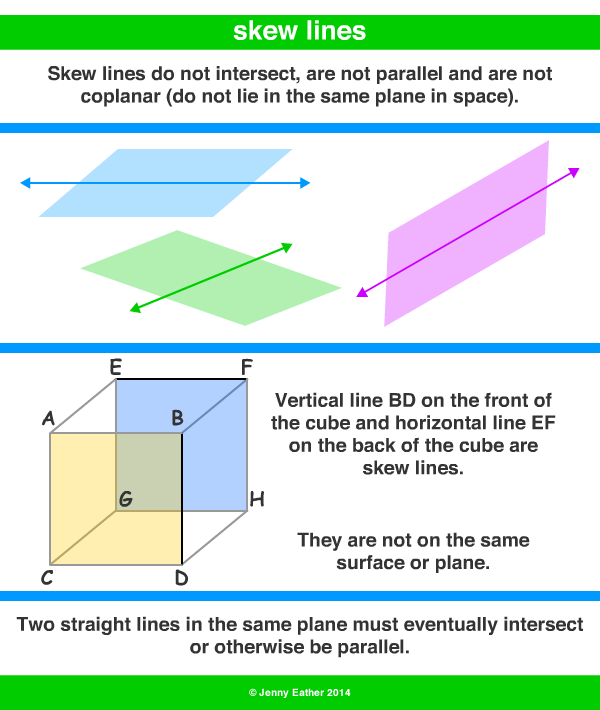
Distance Between Skew Lines
The shortest distance between two skew lines is the length of the line segment that intersects both lines and is perpendicular to both lines. For each pair of skew lines, there is only one line segment that is perpendicular to and intersects both lines.
In the figure above, line segment CD is perpendicular to both lines a and b so its length is the shortest distance between the skew lines a and b above.
Can Lines On Different Planes Be Parallel
In Geometry, a plane is any flat, two-dimensional surface. Two planes that do not intersect are said to be parallel. Parallel planes are found in shapes like cubes, which actually has three sets of parallel planes. But a line and plane can be parallel to each other and two planes can be parallel to each other.
Read Also: What Is Place 5 Themes Of Geography
What Is The Definition Of Skew In Math
geometryskewskew
. In this way, what is skew lines with examples?
Skew lines are straight lines in a three dimensional form which are not parallel and do not cross. An example of skew lines are the sidewalk in front of a house and a line running across the top edge of a side of a house.
Likewise, are skew lines perpendicular? Skew lines are lines that are in different planes and never intersect. A line is said to be perpendicular to another line if the two lines intersect at a right angle. Learn skew line, parallel and perpendicular lines along with skew line exmaples with the help of resources on this page.
Accordingly, which definition best describes skew lines?
Skew lines are two lines that do not intersect and are not parallel. Two lines that both lie in the same plane must either cross each other or be parallel, so skew lines can exist only in three or more dimensions . Two lines are skew if and only if they are not coplanar .
Are parallel lines coplanar?
Two lines are parallel lines if they are coplanar and do not intersect. Lines that are not coplanar and do not intersect are called skew lines. Two planes that do not intersect are called parallel planes.
How Do You Find A Skew Symmetric Matrix
These are the steps to find a skew symmetric matrix:
- Step 1: Firstly, check if it’s a square matrix, as only square matrices can be considered as skew symmetric matrices.
- Step 2: Find the transpose of the given matrix.
- Step 3: Then find the negative of the given matrix.
- Step 4: If the transpose of the matrix is equal to the negative of the given matrix, then it is a skew symmetric matrix.
Recommended Reading: Cpm Algebra 2 Chapter 1 Answers