Developing A Proof In Geometry
Proving statements in mathematics mystifies many students. While some students might feel proofs are hard in general, others will find that taking another approach to proofs can simplify the process. For more visual learners, the flow proof method can demonstrate how each mathematical statement works together to create the final mathematical fact. Doing a flow proof is like drawing a diagram, only with mathematical statements.
Statistical Proof Using Data
“Statistical proof” from data refers to the application of statistics, data analysis, or Bayesian analysis to infer propositions regarding the probability of data. While using mathematical proof to establish theorems in statistics, it is usually not a mathematical proof in that the assumptions from which probability statements are derived require empirical evidence from outside mathematics to verify. In physics, in addition to statistical methods, “statistical proof” can refer to the specialized mathematical methods of physics applied to analyze data in a particle physicsexperiment or observational study in physical cosmology. “Statistical proof” may also refer to raw data or a convincing diagram involving data, such as scatter plots, when the data or diagram is adequately convincing without further analysis.
Colloquial Use Of Mathematical Proof
The expression “mathematical proof” is used by lay people to refer to using mathematical methods or arguing with mathematical objects, such as numbers, to demonstrate something about everyday life, or when data used in an argument is numerical. It is sometimes also used to mean a “statistical proof” , especially when used to argue from data.
Recommended Reading: What Is An Example Of Movement In Geography
Proof That Proofs Belong In Geometry
You probably already know how much I LOVE proofs. It’s my absolute favorite thing to teach. But this post is focused more on why I argue that we should never “water down” or cut back on explicitly teaching formal proofs in Geometry class.The formal proof is a staple of the geometry curriculum. It has also been the center of debate among educators for quite some time.Some educationalists believe that the proof should be abandoned for less formal ways of understanding geometric ideas, while others believe that the emphasis of the formal proof is an integral part of learning geometry.However, any decrease in proof based lessons is an extreme disservice to our students.
First Step Of Indirect Proof
Geometricians such as yourself can get hung up on the very first step, because you have to word your assumption of falsity carefully.
You first need to clue the reader in on what you are doing. Most mathematicians do that by beginning their proof something like this:
- “Assuming for the sake of contradiction that “
- “If we momentarily assume the statement is false “
- “Let us suppose that the statement is false “
Aha, says the astute reader, we are in for an indirect proof, or a proof by contradiction.
Then you have to make certain you are saying the opposite of the given statement. You cannot say more or less than that for the initial assumption.
Read Also: Segment Addition Postulate Worksheet Answers
How To Do Proofs In Geometry
To do a proof in geometry, construct a two-column table. Label the left side Statements and the right side Reasons. Then list all given information in separate lines on the left. On the right write given. Then reflect on what you can conclude from the givens. For example, if youre given an angle bisector, in your statements column, you could indicate that two bisected angles are congruent and in the right column write definition of an angle bisector.
Who are the experts?Our certified Educators are real professors, teachers, and scholars who use their academic expertise to tackle your toughest questions. Educators go through a rigorous application process, and every answer they submit is reviewed by our in-house editorial team.
Like the name suggests, a geometric proof is an attempt to prove a statement with logic. The first step in writing a proof is to construct a chart that has two columns. You should label the left column statements and the right column reasons.
The problem you are given will…
The Structure Of A Proof
Geometric proofs can be written in one of two ways: two columns, or a paragraph. A paragraph proof is only a two-column proof written in sentences. However, since it is easier to leave steps out when writing a paragraph proof, we’ll learn the two-column method.
A two-column geometric proof consists of a list of statements, and the reasons that we know those statements are true. The statements are listed in a column on the left, and the reasons for which the statements can be made are listed in the right column. Every step of the proof is a row in the two-column proof.
Writing a proof consists of a few different steps.
Given:
Read Also: Lesson 1.7 Practice A Geometry Answers
Direct Vs Indirect Proof
An indirect proof can be thought of as “the long way around” a problem. Rather than attack the problem head-on, as with a direct proof, you go through some other steps to try to prove the exact opposite of the statement. You are subtly intending to fail, so that you can then step back and say, “I did my best to show it was false. I could not prove it was false, so it must be true.”
Inductive Logic Proofs And Bayesian Analysis
Proofs using inductive logic, while considered mathematical in nature, seek to establish propositions with a degree of certainty, which acts in a similar manner to probability, and may be less than full certainty. Inductive logic should not be confused with mathematical induction.
Bayesian analysis uses Bayes’ theorem to update a person’s assessment of likelihoods of hypotheses when new evidence or information is acquired.
Read Also: What Is An Example Of Movement In Geography
Tips For Teaching Geometry Proofs
Scaffold, scaffold, scaffold.Phrase everything as a question.
- What kind of angles are these?
- What do we know about linear pairs?
- What postulate allows us to add angle measures?
- How do you know?
Make students keep a Proof Reasons List.Do activities with proofs.Always fill in the given information first.Let students abbreviate.Have students write out theorems.meanHighlight pairs of parallel lines.When using the Substitution Property or Transitive Property, write the line numbers of the statements you are using. Circle words that have definitions.Require that students mark the diagrams.Do you have any tips for helping students write proofs? Leave them in the comments!
Ways To Teach Geometry Proofs
Geometry proofs can be a painful process for many students . Proofs were definitely not my favorite topic to teach. Since they are a major part of most geometry classes, its important for teachers to have effective strategies for teaching proofs.
Here are 5 strategies I used in the classroom to make geometry proofs less painful and easier for students to grasp. Help students learn how to do geometry proofs in no time!
You may also like:
This article contains affiliate links to products. I may receive a commission for purchases made through these links.
Read Also: Kendall Hunt Discovering Geometry Answers
How To Do An Indirect Proof
When is the right time to try an indirect proof or proof by contradiction? When the statement to be proven true can be questioned: “What if interior angles of triangles do not add to 180 ?” Try to prove that when you fail, you have succeeded!
Another handy way to use an indirect proof is when the cases showing the statement to be true are simply too numerous to be practical. Consider an assertion like this:
No integers exist that fulfill, 10
What Harm Does It Do When Proofs Are Removed
Limiting the amount of substantial and challenging proofs in a geometry curriculum pretty much defeats the purpose of the course.Geometrical proofs offer students a clear introduction to logical arguments, which is central to all mathematics. They show the exact relationship between reason and equations.
Recommended Reading: Who Are Paris Jackson’s Biological Parents
What Is An Informal Proof
On the one hand, formal proofs are given an explicit definition in a formal language: proofs in which all steps are either axioms or are obtained from the axioms by the applications of fully-stated inference rules. On the other hand, informal proofs are proofs as they are written and produced in mathematical practice.
Congruency Of Triangles: Asa Sss Sas Aas
-
States, if the two angles and the side included between them of one triangle are equal to the two corresponding angles and the side included between them of another triangle, the two triangles are congruent.
-
states, if the three sides of one triangle are equal to the three corresponding sides of another triangle, the two triangles are congruent.
-
says that If two sides and an included angle of one triangle are congruent to two corresponding sides and an included angle of another triangle, then the triangles are congruent.
-
States, if the hypotenuse and side of one right-angled triangle are equal to the hypotenuse and the corresponding side of another right-angled triangle, the two triangles are congruent.
-
says that If two angles and non-included sides of one triangle are congruent to two angles and a non-included side of another triangle, then the triangles are congruent.
Don’t Miss: Elastic Force Formula
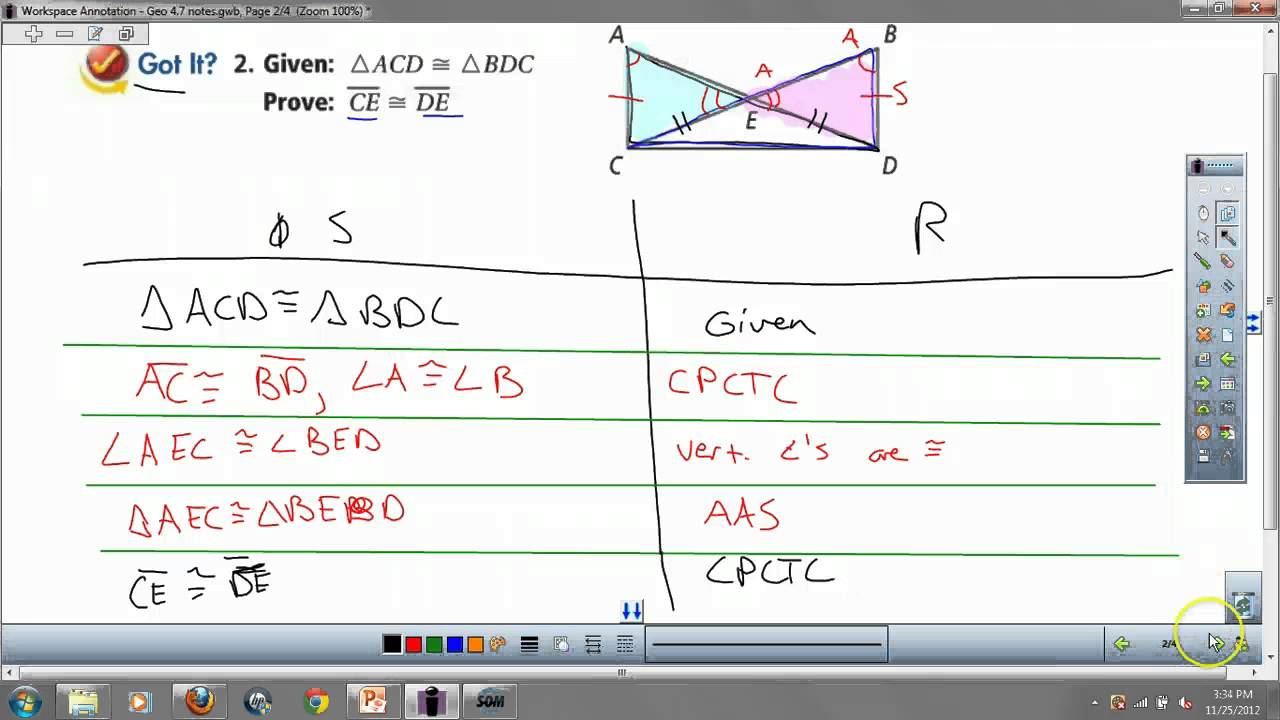
How To Write A Two Column Proof
So what should we keep in mind when tackling two-column proofs?
Always start with the given information and whatever you are asked to prove or show will be the last line in your proof, as highlighted in the above example for steps 1 and 5, respectively.
Remember when you are presented with a word problem its imperative to write down what you know, as it helps to jumpstart your brain and gives you ideas as to where you need to end up?
The same thing is true for proofs.
Start with what you know and this will help to organize your statements and lead you to what you are trying to verify.
Sometimes it is easier to first write down the statements first, and then go back and fill in the reasons after the fact. Other times, you will simply write statements and reasons simultaneously. There is no one-set method for proofs, just as there is no set length or order of the statements.
As long as the statements and reasons make logical sense, and you have provided a reason for every statement, as ck-12 accurately states. As seen in the above example, for every action performed on the left-hand side there is a property provided on the right-hand side. These steps and accompanying reasons make for a successful proof.
Proofs take practice! The more your attempt them, and the more you read and work through examples the better you will become at writing them yourself.
Additionally, its important to know your definitions, , postulates, and theorems.
What Should You Bring To A Formal Proof
Geometry
- A Solid Foundation: Definitions, Postulates, and Theorems
- What Should You Bring to a Formal Proof?
A formal proof of a statement is a sequence of steps that links the hypotheses of the statement to the conclusion of the statement using only deductive reasoning. The hypotheses and conclusion are usually stated in general terms. For example, you have already learned that when two lines intersect, the vertical angles formed are congruent. This statement is vague in that it does not name the specific lines that intersect or give the point of intersection. The statement does not even name the vertical angles formed. Because everything is so general, it’s hard to get a handle on where to start. That’s why in geometry a picture is worth a thousand words. When you draw a picture illustrating what’s going on, it’s easier to see what you are assuming and what you are trying to prove. You can translate your general statement into the picture in Figure 8.1. Here you have two intersecting lines, ?AC and ?BD. They intersect at O. They form a couple of vertical angles, which you’ve named ?AOB and ?DOC. Your mission is to show that these two angles are congruent.
The next step is to interpret what you would like to prove in terms of your picture. The general conclusion is that vertical angles are congruent. In your picture, the vertical angles are ?AOB and ?DOC. You will prove that ?AOB ?= ?DOC.
Solid Facts
Let’s practice writing a formal proof by proving Theorem 8.2.
Figure 8.2
Read Also: What Is The Molecular Geometry Of Ccl4
Proofs As Mental Objects
Psychologism views mathematical proofs as psychological or mental objects. Mathematician philosophers, such as Leibniz, Frege, and Carnap have variously criticized this view and attempted to develop a semantics for what they considered to be the language of thought, whereby standards of mathematical proof might be applied to empirical science.
Sound Overwhelming Read This For Help:
| If proofs intimidate you as a new Geometry teacher, or even if youre a veteran and your kids always struggle through the first weeks of proofs, you are not alone! Its such a tricky new way of thinking for them. But dont skip them! Instead, go about it in a better way. Check out this twist: Its a key step that I added into my introductory unit on proofs for a much smoother transition into teaching proof writing. It made a world of difference for my students.I wrote up this post to guide you through a smoother way to set students up for success with proof writing. Click the image to |
| Looking for even more support? The complete unit I developed includes a presentation and printables to lead your students from the basics , through a special revamped Algebra proof that scaffolds their learning all the way up through writing their first batch of Geometry proofs! This method is the smoothest way to introduce this challenging unit. Check out what’s included in the full unit. |
Also Check: Who Are Paris Jackson’s Biological Parents
How To Do Proofs In Geometry Lesson & Examples
44 min
- How to Write Two-Column Proofs?
- 00:00:25 What is a two column proof?
- 00:08:58
- Complete the two column proof for congruent segments or complementary angles
- 00:29:19 Write a two column proof
- 00:40:53 List of important geometry theorems
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Build On Prior Knowledge

Geometry students have most likely never seen or heard of proofs until your class. They can be so overwhelming at first!
Thats why its a good idea to build on their prior knowledge. Since most geometry students have just taken algebra, I like to start with a few algebra proofs.
Basic algebra proofs help geometry students to see the format, process, and purpose of proofs. I always emphasized to my students that proofs are just a way of organizing the steps to solving a problem.
Remember: dont make these proofs too complicated! The purpose is not to teach or reteach algebra skills. The purpose is to introduce proofs in a way that builds on what students already know.
If you dont have a ton of time to do algebra proofs, even just starting with one or two can help students understand the basics of geometry proofs.
Don’t Miss: Which Pioneer In Psychology Helped Develop The School Of Thought Called Structuralism
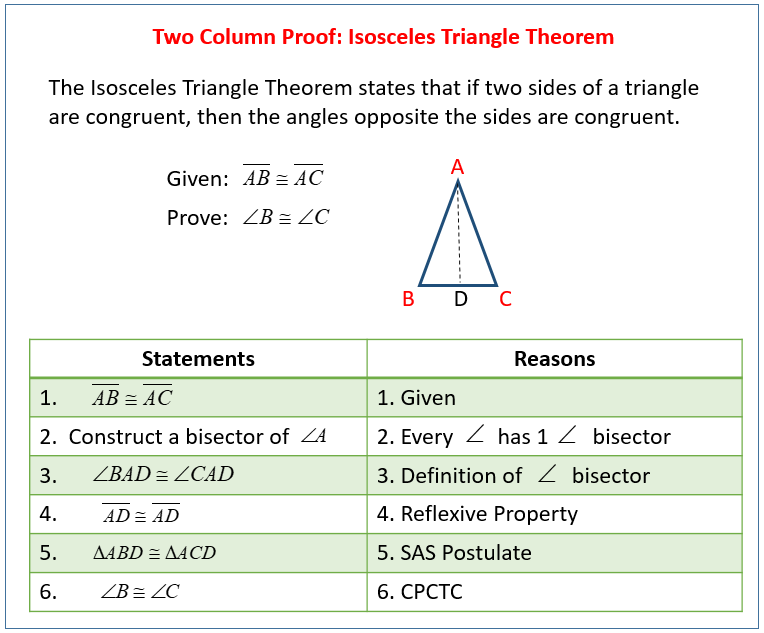
How To Write Two
You can write a two-column proof by drawing a horizontal line at the top of a sheet of paper and a vertical line down the middle. Label the left side “Statement” and the right side “Reason.” Say you are asked to prove the Isosceles Triangle Theorem, which states that if two sides of a triangle are congruent, their opposite angles are congruent.
You will be given some information, like WHZ has Side HW Side HZ, making it an isosceles triangle.
You are asked to prove W Z.
Two-column Proof Example
| W Z | Corresponding parts of congruent triangles are congruent |
This was a five-step proof. Most geometry proofs can be done in fewer than 10 steps. If you find yourself going past, say, seven or eight steps, you may be going down an inefficient or wrong path. How can you help yourself?
Unlock This Answer Now
Start your 48-hour free trial to unlock this answer and thousands more. Enjoy eNotes ad-free and cancel anytime.
Already a member? Log in here.
Like the name suggests, a geometric proof is an attempt to prove a statement with logic. The first step in writing a proof is to construct a chart that has two columns. You should label the left column statements and the right column reasons.
The problem you are given will include a given statement as well as a statement that you have to prove. For example, lets look at the following problem:
Given: Triangle EFG is an isosceles triangle, with base EG. Line FE is congruent to Line FG. Line FH bisects angle EFG.
Prove: Angle E is congruent to Angle G.
Your first statements in your statements column should repeat the given information. In this case, you would write that Line FE is congruent to Line FG. In the reasons section directly to the right, you will write the word given. Then your next line underneath the first one in the statements column will be Line FH bisects angle EFG. Again, you will write given as your reason for this.
For instance, in this example, you can use the reflective postulate to prove that FH is congruent to FH and then the Side Angle Side postulate to prove that Triangle EFH and Triangle GFH are congruent. From there you can prove that Angle E is congruent to Angle G with the reason CPCTC meaning that corresponding parts of congruent triangles are congruent.
Also Check: Geometry Segment Addition Postulate Worksheet