How Do You Do Elimination Method
The Elimination Method
Solving Systems Of Equations By Substitution:
Before we get into using the method of substitution, make sure you’re comfortable with your algebra by reviewing the lesson on solving linear equations with variables on both sides.
The basic procedure behind solving systems via substitution is simple: Given two linear equations, all we need to do is to “substitute” one in the pair of equations into its other by rearranging for variables. This procedure is better outlined below with the general example:
Consider the following equations, with being coordinates and everything else representing constants.
Solving Simultaneous Equations Using The Substitution Method
Several algebraic techniques exist to solve simultaneous equations.
Perhaps the easiest to comprehend is the substitution method.
Take, for instance, our two-variable example problem:
In the substitution method, we manipulate one of the equations such that one variable is defined in terms of the other:
Then, we take this new definition of one variable and substitute it for the same variable in the other equation.
In this case, we take the definition of y, which is 24 – x and substitute this for the y term found in the other equation:
Now that we have an equation with just a single variable , we can solve it using normal algebraic techniques:
Now that x is known, we can plug this value into any of the original equations and obtain a value for y.
Or, to save us some work, we can plug this value into the equation we just generated to define y in terms of x, being that it is already in a form to solve for y:
Applying the substitution method to systems of three or more variables involves a similar pattern, only with more work involved.
This is generally true for any method of solution: the number of steps required for obtaining solutions increases rapidly with each additional variable in the system.
To solve for three unknown variables, we need at least three equations. Consider this example:
Being that the first equation has the simplest coefficients , it seems logical to use it to develop a definition of one variable in terms of the other two.
You May Like: How To Find Ksp From Solubility
What Do We Substitute In The Substitution Method
In the substitution method, we substitute the value of one variable found by simplifying an equation in the other equation. For example, if there are two variables in the equations m and n, then we can first find the value of m in terms of n from any one of the equations, then we substitute that value in the second equation to get an answer of n. Then, we again substitute the value of n in any of the given equations.
Systems Of Linear Equations:
A system of is just a set of two or more linear equations.
In two variables y ) , the graph of a system of two equations is a pair of lines in the plane.
There are three possibilities:
- The lines intersect at zero points.
- The lines intersect at exactly one point.
- The lines intersect at infinitely many points.
How to Solve a System Using The Substitution Method
- Step : First, solve one linear equation for y
- : Then substitute that expression for y in the other linear equation. You’ll get an equation in x
- : Solve this, and you have the x
- to either equation to find the corresponding y
: If it’s easier, you can start by solving an equation for x
Solve the second equation for y
in the first equation and solve for x
: If the lines are parallel, your x -terms will cancel in step 2 , and you will get an impossible equation, something like 0
: If the two equations represent the same line, everything will cancel in step 2 , and you will get a redundant equation, 0 .
Read Also: Why Are There Different Branches Of Chemistry
Solving Systems Of Equations Using Substitution
MA, Stanford UniversityTeaching in the San Francisco Bay Area
Alissa is currently a teacher in the San Francisco Bay Area and Brightstorm users love her clear, concise explanations of tough concepts
If two equations are both in slope-intercept form, you can easily using substitution to solve the system by putting one value of y equal to the other value of y . From there, use inverse operations to solve for x. Once you have the value for x, plug it into either of the two original equations in the system to find the value of y. The x and y values make up the coordinate point of the solution to the system. Check your answer by plugging the x and y value into both equations to see if they are both true.
What Is The Substitution Method In Just 3 Simple Steps
What is the most useful technique for solving a system of equations?
Jenn, Founder Calcworkshop®, 15+ Years Experience
The Substitution Method!
Why?
Because it is used in such topics as nonlinear systems, linear algebra, computer programming, and so much more.
And the greatest thing about solving systems by substitution is that its easy to use!
The method of substitution involves three steps:
Now at first glance, this may seem complicated, but Ive got some helpful tricks for keeping things straight. In fact, were going to make a sort of circular circuit that helps to provide organization and efficiency to our method.
Using the Substitution Method to Solve
Remember, our goal when solving any system is to find the point of intersection. As we saw in our , we saw that some systems do not have solutions because they dont intersect, and others coincide, which provides infinitely many solutions.
So when we solve systems by substitution, we will need to be on the lookout for these types of scenarios. If they are parallel and dont intersect, then we are going to end up with an invalid answer, or as Purple Math calls it, a garbage result.
Also Check: Algebra 1 Eoc Fsa Practice Test No Calculator Portion Answers
What Is Substitution Method
The substitution method is a simple way to solve linear equations algebraically and find the solutions of the variables. As the name suggests, it involves finding the value of x-variable in terms of y-variable and then substituting or replacing the value of x-variable in the second equation. In this way, we can solve and find the value of the y-variable. And at last, we can put the value of y in any of the given equations to find x.
Using The Substitution Method Tosolve Systems Of Equations
The substitution method is one of two ways to solve systems of equations without graphing.
You might ask yourself, “Why wouldn’t I just want to graph the equations to find the solution?” Well there are many reasons…
You may not have graph paper or an accurate way to graph the equations, thus making it hard to identify the solution.
Or, as the equations become more difficult, the solution is not always an identifiable point on the graph. This means that the solution may contain decimals or fractions, which is not easy to identify on a graph.
Once you learn the algebraic method for solving a system of equations, you will probably find that it becomes your preferred method. Graphing becomes too tedious.
The good news is that there are two methods, which makes this process easier depending on the problems you are given.
So, let’s get to it!
The following steps can be used as a guide as you read through the examples for using the substitution method.
Recommended Reading: Are Nutrients Abiotic
How To Solve A System Using The Elimination Method
Example
To solve the system by elimination, what would be a useful first step?
???x+3y=12???
???2x-y=5???
When we use elimination to solve a system, it means that were going to get rid of one of the variables. So we need to be able to add the equations, or subtract one from the other, and in doing so cancel either the ???x???-terms or the ???y???-terms.
Any of the following options would be a useful first step:
Multiply the first equation by ???-2??? or ???2???. This would give us ???2x??? or ???-2x??? in both equations, which will cause the ???x???-terms to cancel when we add or subtract.
Multiply the second equation by ???3??? or ???-3???. This would give us ???3y??? or ???-3y??? in both equations, which will cause the ???y???-terms to cancel when we add or subtract.
Divide the second equation by ???2???. This would give us ???x??? or ???-x??? in both equations, which will cause the ???x???-terms to cancel when we add or subtract.
Divide the first equation by ???3???. This would give us ???y??? or ???-y??? in both equations, which will cause the ???y???-terms to cancel when we add or subtract.
Lets re-do the last example, but instead of the elimination method, use a graph to find the solution.
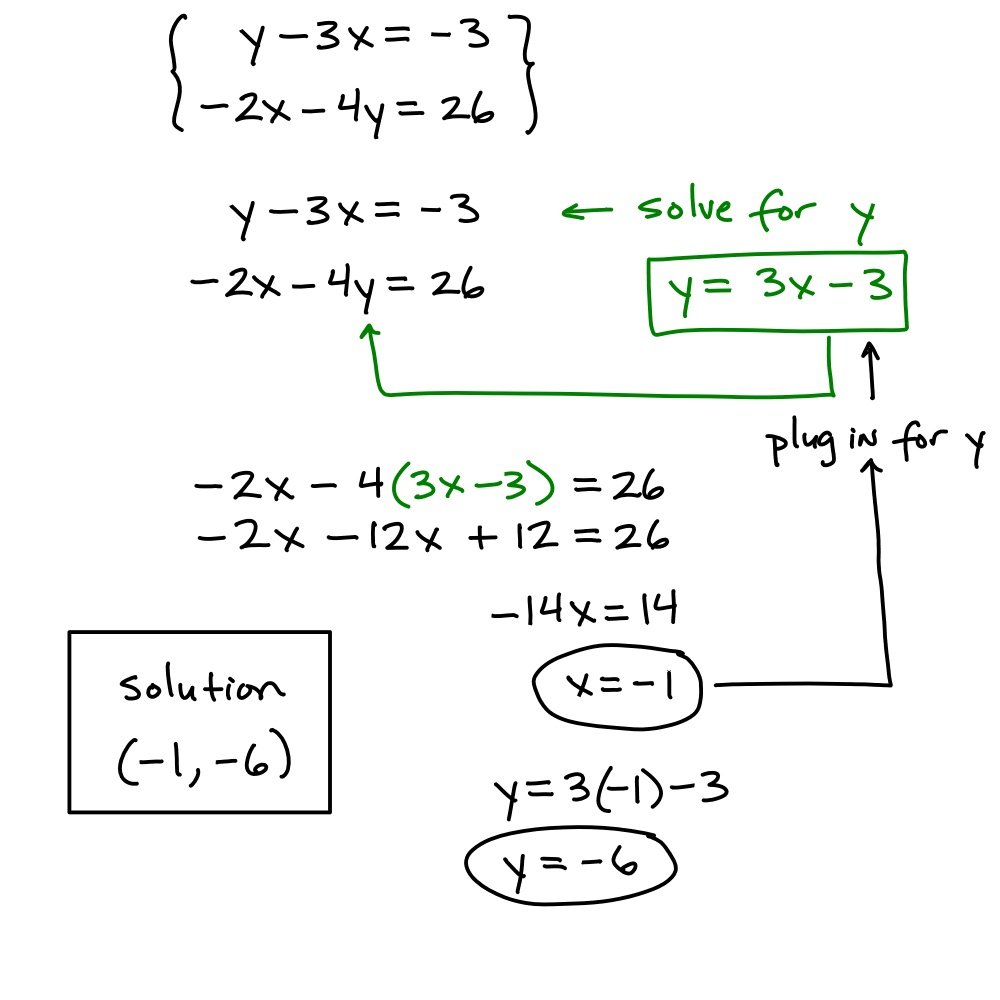
Solve A System Of Equations Using The Substitution Method
In the last couple sections, we verified that ordered pairs were solutions to systems, and we used graphs to classify how many solutions a system of two linear equations had. What if we are not given a point of intersection, or it is not obvious from a graph? Can we still find a solution to the system? Of course you can, using algebra!
In this section we will learn the substitution method for finding a solution to a system of linear equations in two variables. We have used substitution in different ways throughout this course, for example when we were using the formulas for the area of a triangle and simple interest. We substituted values that we knew into the formula to solve for values that we did not know. The idea is similar when applied to solving systems, there are just a few different steps in the process. You will first solve for one variable, and then substitute that expression into the other equation. Lets start with an example to see what this means.
Find the value of x for this system.
Equation A: 4x+3y=14
Equation B: y=2
xy
\begin4x+3y=14\\y=2\,\,\,\,\,\,\,\end
Substitute y=2 into Equation A.
4x+3\left=14
Simplify and solve the equation for x.
\begin4x+6=14\\4x=20\\x=5\,\,\,\end
Answer
x=5
You can substitute a value for a variable even if it is an expression. Heres an example.
Also Check: Eoc Fsa Warm Ups Algebra 1 Answers
The Substitution Method For Solving Linear Systems
A way to solve a linear system algebraically is to use the substitution method. The substitution method functions by substituting the one y-value with the other. We’re going to explain this by using an example.
$$y=2x+4$$
We can substitute y in the second equation with the first equation since y = y.
$$3x+y=9$$
$$3x+\left =9$$
$$5x+4=9$$
$$5x=5$$
$$x=1$$
This value of x can then be used to find y by substituting 1 with x e.g. in the first equation
$$y=2x+4$$
$$y=2\cdot 1}+4$$
$$y=6$$
The solution of the linear system is .
You can use the substitution method even if both equations of the linear system are in standard form. Just begin by solving one of the equations for one of its variables.
Difference Between Substitution Method And Elimination Method

As we know that the substitution method is the process of solving the equation to find the variable value, and the value is substituted in the other equation. In contrast, the elimination method is the process of eliminating the variables in the equation so that the system of the equation can be left as the function of a single variable.
So, the major difference between the substitution and elimination method is that the substitution method is the process of replacing the variable with a value, whereas the elimination method is the process of removing the variable from the system of linear equations.
Recommended Reading: Who Is Generally Recognized As The Founder Of American Psychology
Can The Substitution Method Be Used To Solve The System Of Equations In Three Variables
Generally, while solving the system of equations with three variables, either we can use the substitution method or the elimination method to make the system into the system of two equations with two variables.
To learn about other methods to solve linear equations in two variables, download BYJUS The Learning App. Happy Learning!
Put your understanding of this concept to test by answering a few MCQs. Click Start Quiz to begin!
Select the correct answer and click on the Finish buttonCheck your score and answers at the end of the quiz
What Is The Substitution Method In Math
In algebra, the substitution method is one of the ways to solve linear equations in two variables. In this method, we substitute the value of a variable found by one equation in the second equation. It is very easy to use when we have smaller numbers, but in the case of large numbers or fractional coefficients, it becomes tedious to apply the substitution method.
Also Check: Who Are Paris Jackson’s Biological Parents
Solve A System Of Equations When Multiplication Is Necessary To Eliminate A Variable
Many times adding the equations or adding the opposite of one of the equations will not result in eliminating a variable. Look at the system below.
\begin3x+4y=52\\5x+y=30\end
If you add the equations above, or add the opposite of one of the equations, you will get an equation that still has two variables. So lets now use the multiplication property of equality first. You can multiply both sides of one of the equations by a number that will allow you to eliminate the same variable in the other equation.
We do this with multiplication. Notice that the first equation contains the term 4y, and the second equation contains the term y. If you multiply the second equation by 4, when you add both equations the y variables will add up to 0.
The following example takes you through all the steps to find a solution to this system.
S To Use Substitution Method
The steps to apply or use the substitution method are given below:
Let us assume two linear equations: 2x+3=0 and x+4y+2=0.
Step 1: Simplify the given equation by expanding the parenthesis if needed. So, here we can simplify the first equation to get 2x + 3y + 15 = 0. Now we have two equations as,
2x + 3y + 15 = 0 _____
x + 4y + 2 = 0 ______
Step 2: Solve any one of the equations for any one of the variables. You can use any variable based on the ease of calculation. Suppose we are solving 2nd equation for x. So, we get x = -4y – 2.
Step 3: Substitute the obtained value of x in the other equation. So we are substituting x = -4y-2 in the equation 2x + 3y + 15 = 0, we get, 2 + 3y + 15 = 0.
Step 4: Now, simplify the new equation obtained using arithmetic operations. We get, -8y-4+3y+15=0
-5y + 11 = 0
-5y = -11
y = 11/5
Step 5: Now, substitute the value of y in any of the given equations. Let us substitute the value of y in equation .
x + 4y + 2 = 0
x + 4 × + 2 = 0
x + 44/5 + 2 = 0
x + 54/5 = 0
x = -54/5
Therefore, after solving the given linear equations by substitution method, we get x = -54/5 and y= 11/5.
Don’t Miss: Segment Addition Postulate Coloring Activity
Recognize Systems Of Equations That Have No Solution Or An Infinite Number Of Solutions
When we learned methods for solving linear equations in one variable, we found that some equations didnt have any solutions, and others had an infinite number of solutions. We saw this behavior again when we started describing solutions to systems of equations in two variables.
Recall this example from Module 1 for solving linear equations in one variable:
Solve for x. 12+2×8=7x+55x
\displaystyle \begin12+2x-8=7x+5-5x\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,2x+4=2x+5\end
\begin\,\,\,\,\,\,\,\,\,\,\,\,2x+4=2x+5\\\,\,\,\,\,\,\,\,\underline\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4= \,5\end
This false statement implies there are no solutions to this equation. In the same way, you may see an outcome like this when you use the substitution method to find a solution to a system of linear equations in two variables. In the next example, you will see an example of a system of two equations that does not have a solution.
Solve for x and y.
\beginy=5x+4\\10x2y=4\end
y
\beginy=5x+4\\10x2y=4\,\,\,\,\,\,\,\,\,\,\,\,\\10×2\left=4\,\,\,\,\,\,\,\,\,\,\,\,\end
Expand the expression on the left.
10x10x8=4
Combine like terms on the left side of equation.
10x10x=0, so you are left with 8=4.
\begin08=4\\8=4\end
Answer
The statement 8=4 is false, so there is no solution.
You get the false statement 8=4. What does this mean? The graph of this system sheds some light on what is happening.
What Are Simultaneous Equations And Systems Of Equations
The terms simultaneous equations and systems of equations refer to conditions where two or more unknown variables are related to each other through an equal number of equations.
Example:
For this set of equations, there is but a single combination of values for x and y that will satisfy both.
Either equation, considered separately, has an infinitude of valid solutions, but together there is only one. Plotted on a graph, this condition becomes obvious:
Each line is actually a continuum of points representing possible x and y solution pairs for each equation.
Each equation, separately, has an infinite number of ordered pair solutions. There is only one point where the two linear functions x + y = 24 and 2x – y = -6 intersect , and that is where x is equal to a value of 6 and y is equal to a value of 18.
Usually, though, graphing is not a very efficient way to determine the simultaneous solution set for two or more equations. It is especially impractical for systems of three or more variables.
In a three-variable system, for example, the solution would be found by the point intersection of three planes in a three-dimensional coordinate spacenot an easy scenario to visualize.
Recommended Reading: Exponential Growth And Decay Common Core Algebra 1 Homework Answers