Graphing A System Of Nonlinear Inequalities
Now that we have learned to graph nonlinear inequalities, we can learn how to graph systems of nonlinear inequalities. A system of nonlinear inequalities is a system of two or more inequalities in two or more variables containing at least one inequality that is not linear. Graphing a system of nonlinear inequalities is similar to graphing a system of linear inequalities. The difference is that our graph may result in more shaded regions that represent a solution than we find in a system of linear inequalities. The solution to a nonlinear system of inequalities is the region of the graph where the shaded regions of the graph of each inequality overlap, or where the regions intersect, called the feasible region.
How to: Given a system of nonlinear inequalities, sketch a graph
Example \: Graphing a System of Inequalities
Graph the given system of inequalities.
Solution
These two equations are clearly parabolas. We can find the points of intersection by the elimination process: Add both equations and the variable \ will be eliminated. Then we solve for \.
Substitute the \-values into one of the equations and solve for \.
Figure \
Graphing A Nonlinear Inequality
All of the equations in the systems that we have encountered so far have involved equalities, but we may also encounter systems that involve inequalities. We have already learned to graph linear inequalities by graphing the corresponding equation, and then shading the region represented by the inequality symbol. Now, we will follow similar steps to graph a nonlinear inequality so that we can learn to solve systems of nonlinear inequalities. A nonlinear inequality is an inequality containing a nonlinear expression. Graphing a nonlinear inequality is much like graphing a linear inequality.
Recall that when the inequality is greater than, \,or less than, \,the graph is drawn with a dashed line. When the inequality is greater than or equal to, \,or less than or equal to, \,the graph is drawn with a solid line. The graphs will create regions in the plane, and we will test each region for a solution. If one point in the region works, the whole region works. That is the region we shade ).
Figure \: an example of \ an example of \ an example of \ an example of \
How to: Given an inequality bounded by a parabola, sketch a graph
Solution
Intersection Of A Parabola And A Line
There are three possible types of solutions for a system of nonlinear equations involving a parabola and a line.
Possible Types of Solutions For Points of Intersection of a Parabola and a Line
Figure \ illustrates possible solution sets for a system of equations involving a parabola and a line.
- No solution – The line will never intersect the parabola.
- One solution – The line is tangent to the parabola and intersects the parabola at exactly one point.
- Two solutions – The line crosses on the inside of the parabola and intersects the parabola at two points.
Figure \
How to: Given a system of equations containing a line and a parabola, find the solution
Example \: Solving a System of Nonlinear Equations Representing a Parabola and a Line
Solve the system of equations.
Solution
Solve the first equation for \ and then substitute the resulting expression into the second equation.
Expand the equation and set it equal to zero.
Solving for \ gives \ and \. Next, substitute each value for \ into the first equation to solve for \. Always substitute the value into the linear equation to check for extraneous solutions.
The solutions are \\) and \\),which can be verified by substituting these \\) values into both of the original equations ).
Figure \
For \
For \
Exercise \
Recommended Reading: Beth Thomas Father Jailed
Linear Vs Nonlinear Functions
Functions can be classified in two different categories: linear or nonlinear. A simple way to know differentiate between the two is to look at the output values when plugging in a number for an unknown variable. If the output values have a difference that is constant, then the function will be classified as a linear equation however, if the outputs do not have a constant difference then it will be classified as a nonlinear equation.
Another easy way to determine which of these functions you are dealing with is to graph it. By graphing these functions, you can tell if the line is straight or not. When graphed, a linear equation will have a straight line that has a constant slope. In contrast to this, a nonlinear equation will have a graph that does not have a straight line and, depending on the function, can have many different appearances including a U-shape or an S-shape.
Look at this example:
Equation: 2x+6=y
As you can see in this example, the differences between the outputs are constant with each increasing number plugged into x. Also, when you graph this equation you will see a straight line that shows that as x increases by 1, y increases by 2 therefore, this is a linear equation.
Compare to this example:
Equation: x2
How Do You Determine If An Equation Is Linear
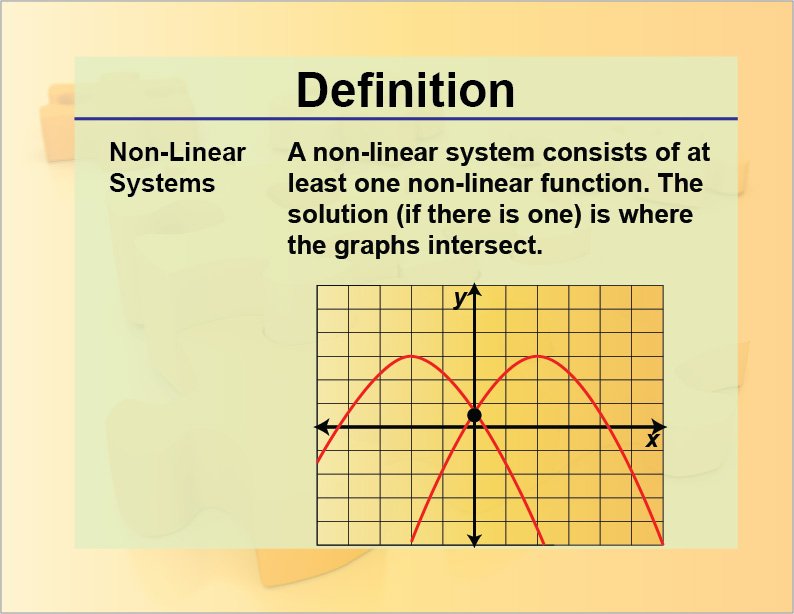
To determine whether the given equation is linear we have to determine that a given equation is in the format y = mx + c where m is the slope x and y are the variables c is the y-intercept. For example y = 2x + 1, here the equation has the highest degree as one So it is a linear equation. A nonlinear equation will not match this equation.
Recommended Reading: Paris Jackson Adopted
Which Equations Are Linear
It is also known as a one-degree equation. The standard form of a linear equation in one variable is of the form Ax + B = 0. Here, x is a variable, and A and B are constants. The standard form of a linear equation in two variables is of the form Ax + By = C.Linear Equations.
| FAQs on Linear Equations |
What’s The Difference Between Linear And Nonlinear Equations
Linear and nonlinear equations usually consist of numbers and variables. A variable is a quantity which could be any integer value. Linear means something related to a line. All the linear equations are used to define or construct a line. A non-linear equation is such which does not form a straight line.
You May Like: Unit 1 Geometry Basics Homework 2 Segment Addition Postulate
What Are Linear Text Examples
Some examples of linear texts include novels, poems, letters, textbooks, etc. In contrast, flow charts, knowledge maps, digital texts with hyperlinks, and encyclopedias are some examples of nonlinear text. Furthermore, non-linear allows readers to you to find specific information more quickly and efficiently.
Linear And Nonlinear Equations
We have learned about equations in the earlier classes. An equation is a statement of the equality of two expressions. The two sides of the equality sign are referred to as the left-hand side and the right-hand side of the equation.
For example, in the equation 3x + 4 = 8, where 3, 4, and 8 are the constants, and x is the variable. The LHS is given by the expression 3x + 4 and the RHS is given by the constant 8. The equation remains unchanged if we carry out the same operation on both sides of the equation.
To solve an equation, we carry out a series of identical Mathematical operations on two sides of the equation such that the unknown variable is one side and its value is obtained on the other side.
Equation: An equation is a statement of equality of two algebraic expressions involving constants and variables.
Based on the degree and variable in the equations, they are classified as linear and nonlinear equations.
You May Like: Prentice Hall Gold Algebra 1 Teaching Resources Answers Chapter 9
What Is Nonlinear Load
A load is considered non-linear if its impedance changes with the applied voltage. These non- sinusoidal currents contain harmonic currents that interact with the impedance of the power distribution system to create voltage distortion that can affect both the distribution system equipment and the loads connected to it.
Solving A System Of Nonlinear Equations Using Substitution
A system of nonlinear equations is a system of two or more equations in two or more variables containing at least one equation that is not linear. Recall that a linear equation can take the form \. Any equation that cannot be written in this form in nonlinear. The substitution method we used for linear systems is the same method we will use for nonlinear systems. We solve one equation for one variable and then substitute the result into the second equation to solve for another variable, and so on. There is, however, a variation in the possible outcomes.
Read Also: Ccl4 Molecular Shape
What Is A Nonlinear Function
A nonlinear function is a function whose graph is NOT a straight line. Its graph can be any curve other than a straight line. For example, if there are 100 fishes in a pond initially and they become double every week, then this situation can be modeled by the function f = 100 x, where x is the number of weeks and f is the number of fishes. Let us make a table and graph this function making use of the table.
| x |
|---|
| 800 |
Let’s graph the table now.
The above graph is NOT a line and hence it represents a nonlinear function. From the above graph, we can say that the slope is not uniform on a nonlinear function. A nonlinear function can be described using a table of values, an equation, or a graph. Let us see each of them now. Some of the examples of non linear functions include quadratic functions, cubic functions, polynomial functions.
Solving A System Of Nonlinear Equations Using Elimination
We have seen that substitution is often the preferred method when a system of equations includes a linear equation and a nonlinear equation. However, when both equations in the system have like variables of the second degree, solving them using elimination by addition is often easier than substitution. Generally, elimination is a far simpler method when the system involves only two equations in two variables , rather than a three-by-three system, as there are fewer steps. As an example, we will investigate the possible types of solutions when solving a system of equations representing a circle and an ellipse.
POSSIBLE TYPES OF SOLUTIONS FOR THE POINTS OF INTERSECTION OF A CIRCLE AND AN ELLIPSE
Figure \ illustrates possible solution sets for a system of equations involving a circle and an ellipse.
- No solution – The circle and ellipse do not intersect. One shape is inside the other or the circle and the ellipse are a distance away from the other.
- One solution – The circle and ellipse are tangent to each other, and intersect at exactly one point.
- Two solutions – The circle and the ellipse intersect at two points.
- Three solutions – The circle and the ellipse intersect at three points.
- Four solutions – The circle and the ellipse intersect at four points.
Figure \
Also Check: Holt Geometry Chapter 7
What Is The Difference Between A Linear And Non
With a linear load, the relationship between the voltage and current waveforms are sinusoidal and the current at any time is proportional to the voltage . On the other hand, with a non-linear load the current isnt proportional to the voltage and it fluctuates based on the alternating load impedance.
What Is The Difference Between Linear And Nonlinear Equations
To find the difference between the two equations, i.e. linear and nonlinear, one should know the definitions for them. So, let us define and see the difference between them.
| Linear Equations |
|
Note:
The linear equation has only one variable usually and if any equation has two variables in it, then the equation is defined as a Linear equation in two variables. For example, 5x + 2 = 1 is Linear equation in one variable. But 5x + 2y = 1 is a Linear equation in two variables.
Let us see some examples based on these concepts.
Recommended Reading: Prince Jackson Mom
What Forms A Linear Equation
The simplest form of a linear equation can be explained in the form y = a + bx where both a and b represent constants in an equation while there will be two variables that will be present. This forms the backbone of the linear equation. This linear equation when it is plotted on a graph paper will yield you a straight line with the line passing through the origin. It will have a constant slope value throughout the straight line that is passing through the origin.
Types Of Nonlinear Dynamic Behaviors
- Amplitude death â any oscillations present in the system cease due to some kind of interaction with other system or feedback by the same system
- Chaos â values of a system cannot be predicted indefinitely far into the future, and fluctuations are aperiodic
- Multistability â the presence of two or more stable states
- Solitons â self-reinforcing solitary waves
- Limit cycles â asymptotic periodic orbits to which destabilized fixed points are attracted.
- Self-oscillations – feedback oscillations taking place in open dissipative physical systems.
Recommended Reading: Kuta Software Simplifying Radicals Answers
How Do You Know If A Data Is Linear Or Not
In case you are dealing with predicting numerical value, the technique is to use scatter plots and also apply simple linear regression to the dataset and then check least square error. If the least square error shows high accuracy, it can be implied that the dataset is linear in nature, else the dataset is non-linear.
Difference Between Linear And Nonlinear Equations
In Mathematics, you must have learned about different types of equations. Here, we are going to discuss the difference between linear and nonlinear equations. The difference between them is described here with the help of definitions and examples.
We come across a lot of equations while solving maths problems. Some equations include only numbers and some consist of only variables while others consist of both numbers and variables. Linear and nonlinear equations usually consist of numbers and variables.
Recommended Reading: Why Was The Pail Pale Answers
Definition Of Linear And Non
Linear means something related to a line. All the linear equations are used to construct a line. A non-linear equation is such which does not form a straight line. It looks like a curve in a graph and has a variable slope value.
The major difference between linear and nonlinear equations is given here for the students to understand it in a more natural way. The differences are provided in a tabular form with examples.
Differentiate Between Linear And Nonlinear Equations
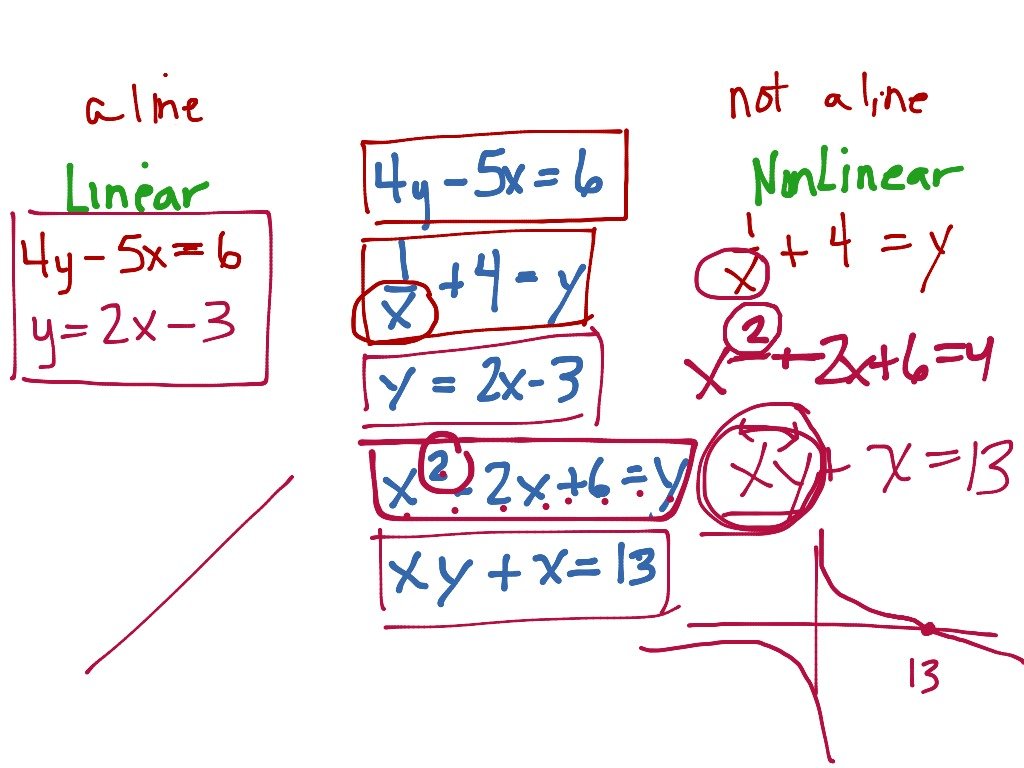
|
Linear Equations |
Non-Linear Equations |
|
A Linear equation can be defined as the equation having the maximum of only one degree. |
A Nonlinear equation can be defined as the equation having the maximum degree 2 or more than 2. |
|
A linear equation forms a straight line on the graph. |
A nonlinear equation forms a curve on the graph. |
|
The general form of linear equation is, y = mx +c Where x and y are the variables, m is the slope of the line and c is a constant value. |
The general form of nonlinear equations is, ax2 + by2 = c Where x and y are the variables and a,b and c are the constant values |
|
Examples: |
Let us understand what are linear and nonlinear equations with the help of some examples.
Example1: Solve the Linear equation 9 = 2
Solution:
Subtract 6x from both the sides
9x + 9 – 6x = 6x + 16 – 6x
3x + 9 = 16
Substract 9 from both the sides
3x + 9 – 9 = 16 – 9
3x = 7
Example 2 : Solve the nonlinear equation
3×2 – 5x + 2 = 0
3×2 – 3x – 2x + 2 = 0
3x – 2 = 0
= 0 or = 0
x = 2/3 or x = 1
Recommended Reading: What Are The Four Main Areas Of Biological Contamination
What Is Linear Example
Linear equations are equations of the first order. A linear equation can have more than one variable. If the linear equation has two variables, then it is called linear equations in two variables and so on. Some of the examples of linear equations are 2x 3 = 0, 2y = 8, m + 1 = 0, x/2 = 3, x + y = 2, 3x y + z = 3.
Midas With Minmeanmax Effects
Next we consider an example of a parametric nonlinear model where the nonlinearity is induced by the relative size of high-frequency observation among i = 0k and not by their joint aggregate as in the LSTR-MIDAS. Whenever there is a choice of aggregation function of higher-frequency variables , it is often unclear whether some average, minimum, maximum, or some combination should be used? In a nonlinear MIDAS framework, one can get the answer to this question using an extended MIDAS aggregation function along the lines proposed in Kvedaras and Rakauskas . For that purpose, let us replace in Eq. the usual MIDAS restriction function h by
R. Wehrens, in, 2009
You May Like: Michael Jackson Biological Father