What Is Elasticity In Physics

Example : The Stretch Of A Long Cable

Suspension cables are used to carry gondolas at ski resorts. Consider a suspension cable that includes an unsupported span of 3 km. Calculate the amount of stretch in the steel cable. Assume that the cable has a diameter of 5.6 cm and the maximum tension it can withstand is\boldsymbol}.

Figure 4.

Strategy

The force is equal to the maximum tension, or\boldsymbol}.The cross-sectional area is\boldsymbol^2=2.46\times10^\textbf^2}.The equation\boldsymbol=\frac\fracL_0}can be used to find the change in length.

Solution

All quantities are known. Thus,

Discussion

This is quite a stretch, but only about 0.6% of the unsupported length. Effects of temperature upon length might be important in these environments.

Figure 5.

Example : Calculating Deformation: How Much Does Your Leg Shorten When You Stand On It

Calculate the change in length of the upper leg bone when a 70.0 kg man supports 62.0 kg of his mass on it, assuming the bone to be equivalent to a uniform rod that is 40.0 cm long and 2.00 cm in radius.

Strategy

The force is equal to the weight supported, or

and the cross-sectional area is\boldsymbol^2=1.257\times10^\textbf^2}.The equation\boldsymbol=\frac\fracL_0}can be used to find the change in length.

Solution

All quantities except\boldsymbol}are known. Note that the compression value for Youngs modulus for bone must be used here. Thus,

Discussion

This small change in length seems reasonable, consistent with our experience that bones are rigid. In fact, even the rather large forces encountered during strenuous physical activity do not compress or bend bones by large amounts. Although bone is rigid compared with fat or muscle, several of the substances listed in Table 3 have larger values of Youngs modulus\boldsymbol.In other words, they are more rigid.

The equation for change in length is traditionally rearranged and written in the following form:

The ratio of force to area,\boldsymbol},is defined as stress, and the ratio of the change in length to length,\boldsymbol}},is defined as strain . In other words,

In this form, the equation is analogous to Hookes law, with stress analogous to force and strain analogous to deformation. If we again rearrange this equation to the form

we see that it is the same as Hookes law with a proportionality constant

Elastic Constants Of Iron As A Function Of Pressure At Zero Kelvin

The elastic constants of hcp-Fe at 39 and 211 GPa and ambient temperature have been measured experimentally . Calculations of elastic constants at 0 K for hcp-Fe have been reported by Stixrude and Cohen , Söderlind et al , Steinle-Neumann et al. , and Voadlo et al. . These values are plotted as a function of density in Figure 14 and 14. Although there is some scatter on the reported values of c12, overall the agreement between the experimental and various ab initio studies is excellent.

Figure 14. Combined plot of the elastic constants of hcp-Fe as a function of density calculated at 0 K from Stixrude and Cohen , Söderlind et al , Steinle-Neumann et al. , and Voadlo et al. together with the experimental values of Mao et al. c11 black diamonds, c12 white squares, c44 black circles, c33 white diamonds, c13 black squares, and c66 white circles.

The resulting bulk and shear moduli and the seismic velocities of hcp-Fe as a function of pressure are shown in Figures 15 and 16, along with the experimental data. The calculated values compare well with the experimental data at higher pressures the discrepancies at lower pressures are probably due to the neglect of magnetic effects in the simulations .

Sanjeev Rajput, Naresh Kumar Thakur, in, 2016

Recommended Reading: What Is Learning Theory In Psychology

What Is A Strain

A body subjected to stress gets deformed. The fractional change in the dimension of a body is produced by the external stress acting on is called strain. The ratio of change of any dimension to its original dimension is called the strain. Since strain is the ratio of two identical dimensions, therefore strain is a unitless quantity.

Mathematically, the strain is given by:

The strain is again classified into three types:

Elasticity: Stress And Strain

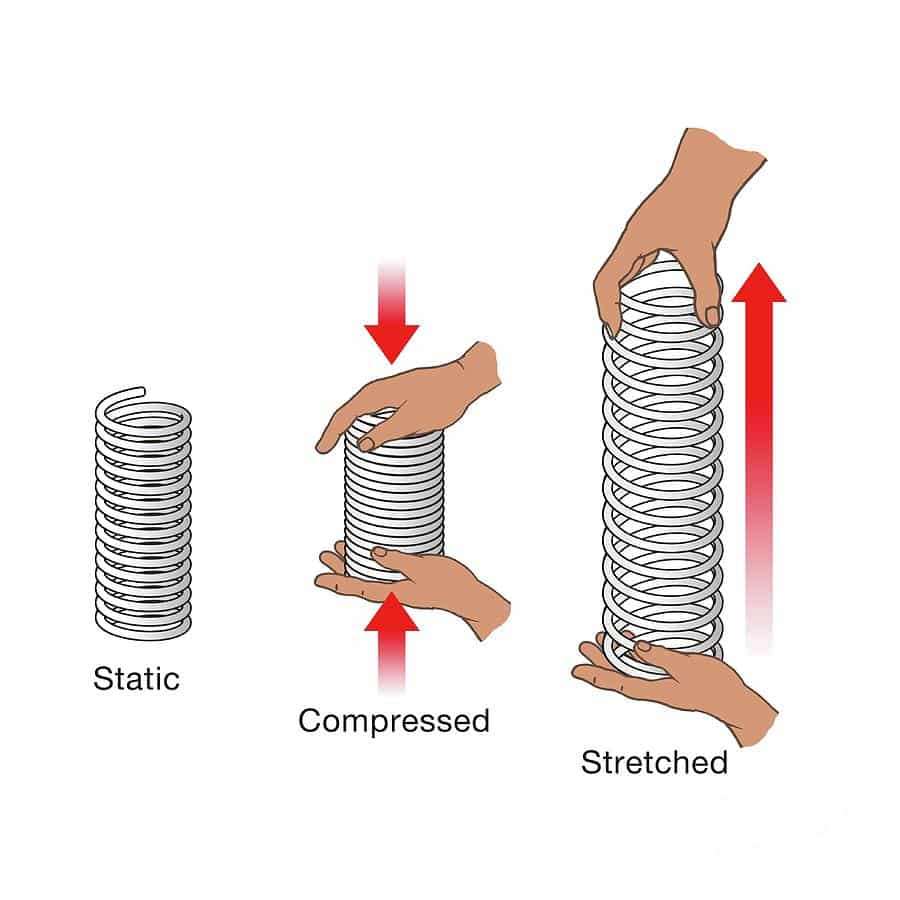
• State Hookes law.
• Explain Hookes law using graphical representation between deformation and applied force.
• Discuss the three types of deformations such as changes in length, sideways shear and changes in volume.
• Describe with examples the youngs modulus, shear modulus and bulk modulus.
• Determine the change in length given mass, length and radius.

deformationHookes law

F = kL,

LFkLL

Read Also: Girls Get Curves Geometry Takes Shape

Hookes Law For Elastic Limit

According to the experimental study done by Hooke in connection with the extension produced in the wire and load applied, he devised a law known by his name called the Hookes law.

Hookes Law statement: Within the elastic limit, the extension produced in the wire is directly proportional to the load applied to it.

After some time, this law became applicable to all types of deformations like compression, bending and twisting, etc. In mathematical form, Hookes law states that in the elastic limit, stress developed is directly proportional to the strain produced in the body. It is given by:

Stress Strain

Now, removing the sign of proportionality, we get the equation as:

Stress = E x Strain

Here, E is proportionality constant and is called the coefficient of elasticity or the Modulus of Elasticity of the material of the body.

Also, E= stress/ strain = a constant

Here, the stress is the deforming force applied per unit area and strain is the deformation that occurred. Therefore, stress and strain are interlinked.

The unit of stress is Nm² and that of strain is unity .

On Elasticity Pdf For Exam

Elasticity is a property of matter that explains the deformation of materials. Whenever a force is exerted on a solid it undergoes deformation. When an external force is applied to a rigid body there will be a change in its length, volume, shape. The change in parameters depends upon the ratio of applied stress to the resulting strain. When the external forces are removed from the body it tends to regain its original shape and size. Such a property of a material by virtue of which the body tends to regain its original shape, size as a result of removal of external forces is known as the elasticity.

You May Like: What Is Delta X In Physics

What This Term Used In Physics Engineering And Chemistry Means

Eric Raptosh Photography/Getty Images

• Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
• B.A., Physics and Mathematics, Hastings College

Elasticity is a physical property of a material whereby the material returns to its original shape after having been stretched out or altered by force. Substances that display a high degree of elasticity are termed “elastic.” The SI unit applied to elasticity is the pascal , which is used to measure the modulus of deformation and elastic limit.

The causes of elasticity vary depending on the type of material. Polymers, including rubber, may exhibit elasticity as polymer chains are stretched and then subsequently return to their original form when the force is removed. Metals may display elasticity as atomic lattices change shape and size, again, returning to their original form once energy is removed.

Examples: Rubber bands and elastic and other stretchy materials display elasticity. Modeling clay, on the other hand, is relatively inelastic and retains a new shape even after the force that caused it to change is no longer being exerted.

Static Equilibrium And Elasticity

• Explain the limit where a deformation of material is elastic
• Describe the range where materials show plastic behavior
• Analyze elasticity and plasticity on a stress-strain diagram

We referred to the proportionality constant between stress and strain as the elastic modulus. But why do we call it that? What does it mean for an object to be elastic and how do we describe its behavior?

Elasticity is the tendency of solid objects and materials to return to their original shape after the external forces causing a deformation are removed. An object is elastic when it comes back to its original size and shape when the load is no longer present. Physical reasons for elastic behavior vary among materials and depend on the microscopic structure of the material. For example, the elasticity of polymers and rubbers is caused by stretching polymer chains under an applied force. In contrast, the elasticity of metals is caused by resizing and reshaping the crystalline cells of the lattices under the action of externally applied forces.

Our perception of an elastic material depends on both its elastic limit and its elastic modulus. For example, all rubbers are characterized by a low elastic modulus and a high elastic limit hence, it is easy to stretch them and the stretch is noticeably large. Among materials with identical elastic limits, the most elastic is the one with the lowest elastic modulus.

Also Check: What Does Converse Mean In Geometry

What Is Elastic Limit In Physics

As we got the stress-strain relationship in wire, now lets understand what elastic limit means in Physics.

Suspend a wire of uniform area vertically from a rigid support and on the other end, attach a hanger on which known weights can be placed. Now, attach a vernier scale V to the wires lower end that can slide over the main scale M, as we can see in Fig.1 below:

Further, keep trying with different weights, place them one-by-one on the hanger, and note the reading.

After noting down the readings of extensions caused by different known weights on the wire, draw a graph. Going according to the reading, we plot the graph in the following manner:

Looking at Graph.1, till the portion OA, the Hookes law is fully obeyed, which means, the wire could gain its configuration. Therefore, OA is a linear region that represents the elastic limit.

As the stress doubles, the strain also doubles, as seen in Graph 2, a non-linear relationship is maintained between the stress and strain. Here, point A is considered the proportional limit. But what is the limit of proportionality?

Youngs Modulus Of Elasticity Y

Within the elastic limit, the ratio of longitudinal stress and longitudinal strain is called Youngs modulus of elasticity .

Within the elastic limit, the force acting upon a unit area of a wire by which the length of wire becomes double is equivalent to Youngs modulus of elasticity of the material of the wire. If L is the length of wire, r radius and is the increase in the length of wire by suspending a weight at its one end then youngs modulus of elasticity of the wire becomes,

The increment of the length of an object by its own weight:

Let a rope of mass M and length is hanged vertically. As the tension of different point on the rope is different, similarly stress as well as the strain will be different at different points.

• Maximum stress at hanging point
• Minimum stress at a lower point

Consider a dx element of rope at x distance from the lower end, then tension

So stress

Let the increase in length of element dx is dy then

Now we got stress and strain then youngs modulus of elasticity y

The total change in length of the wire is

Work done in stretching a wire

If we need to stretch a wire, we have to do work against its inter atomic forces, which is stored in the form of elastic potential energy.

For a wire of length stretched by a distance the restoring elastic force is

Work required for increasing an element length

Total work required in stretching the wire is

Analogy of rod as a spring

From definition of youngs modulus

This expression is analogy of spring force

Recommended Reading: How To Find Biological Grandparents Uk

Difference Between Elastic Limit And Proportional Limit

The difference between elastic limit and the proportional limit is that elastic limit is the greatest pressure that can be applied to a material without causing its deformation. Whereas, the point up to which the stress and strain are directly proportional to each other is referred to as the proportional limit of that material. Another key difference is that in the case of elastic limit the stress and strain possess a linear relationship, while in the case of the proportional limit it does not matter if the relationship between the stress and strain is linear or not.

Sideways Stress: Shear Modulus

Figure illustrates what is meant by a sideways stress or a shearing force. Here the deformation is called \ and it is perpendicular to \, rather than parallel as with tension and compression. Shear deformation behaves similarly to tension and compression and can be described with similar equations. The expression for shear deformation is

where \ is the shear modulus and \ is the force applied perpendicular to \ and parallel to the cross-sectional area \. Again, to keep the object from accelerating, there are actually two equal and opposite forces \ applied across opposite faces, as illustrated in Figure. The equation is logicalâfor example, it is easier to bend a long thin pencil ) than a short thick one, and both are more easily bent than similar steel rods ).

SHEAR DEFORMATION

\ where \ is the shear modulus and \ is the force applied perpendicular to \ and parallel to the cross-sectional area \.

Examination of the shear moduli in Table reveals some telling patterns. For example, shear moduli are less than Youngâs moduli for most materials. Bone is a remarkable exception. Its shear modulus is not only greater than its Youngâs modulus, but it is as large as that of steel. This is why bones are so rigid.

Example\: Calculating Force Required to Deform: That Nail Does Not

Bend much Under a Load.

Find the mass of the picture hanging from a steel nail as shown in Figure, given that the nail bends only \.

Strategy.

Solution

Discussion

You May Like: What Is Water Bath In Chemistry

What Is Plasticity Of Solids

Plasticity is a concept that is opposite to the concept of Elasticity.

Plasticity is a mechanical property of solid by virtue of which it cannot regain its original shape even after external force is removed.

The more a solid showcases this feature of not regaining its original shape, the more plastic its said to be. For example, once we change the shape and size of a lump of putty or mud, it does not regain its original shape. They get permanently deformed. Such solids are often referred to as plastic.

Some Facts

• Almost perfect elastic bodies – Quartz and Phosphor bronze
• Almost perfect plastic bodies – Putty and Mud
• Steel is more elastic than rubber.

Note

What Is Elasticity Of Solids

We know that, when we apply sufficient external force on a solid, its shape and size may change . Such deformation is called elastic deformation.

Law of elasticity or Hooke’s law

Robert Hooke conducted some experiments on springs. He found out that change in length in springs is proportional to the applied external force. This is called Law of elasticity or Hookes law.

Elasticity is a mechanical property of solid by virtue of which it regains its original shape after external force is removed.

The more a solid showcases this feature of regaining its original shape, the more elastic its said to be. For example, when we pull a spring, it stretches . But as soon as we stop pulling it, it regains its original size and shape to some extent. Such solids are often referred to as elastic.

Reason behind Elasticity

We can explain the phenomenon of Elasticity in solids in terms of microscopic nature of the solid.Atoms and Molecules in a solid are close together and bonded together by interatomic or intermolecular forces, and stay in a stable equilibrium position.

Application of force disturbs this equilibrium, and leads to changes in interatomic or intermolecular distances.

But as soon as this external force is removed, the interatomic or intermolecular forces pull back those atoms/molecules to their original positions. Elastic solids regain their original shape and size because of this phenomenon.

Limit of elasticity

You May Like: When Does Your Biological Clock Start Ticking

Difference Between Proportional Limit And Yield Point

Proportional limit or the limit of proportionality specifies the direct relation of stress with strain. Till this point, Hookes law is fully obeyed.

However, a point at which the stress remains constant, while the strain keeps on elongating the wire, a time comes when it reaches the perfectly plastic stage. This stage occurs at the point called the yield point.

Bouncing Ball Physics: What Is Elasticity

What makes a ball bouncy? Have you ever wondered why some balls bounce higher than others? A balls ability to bounce has a lot to do with its elasticity. So what is elasticity? Its an objects ability to return to its original shape after being stretched or squeezed. Objects that are more stretchy are usually more elastic, too. Do you have pajama pants with elastic material in the top? You can stretch to get into them, but they will shrink back to fit your waist!

In this science fair project, well investigate bouncing ball physics to determine which ball has the highest elasticity and find out how elasticity contributes to bounce height.

Don’t Miss: How Can I Find My Biological Mom

Elasticity In Physics With Example

EQTip18 Earthquake Engineering Elasticity Equations of Elasticity Readings: R 2.3, 2.6, 2.8 T & G example: Step 1: consider how elastic components just by describing a material in An example of elasticity is the ability of a womans stomach to stretch during pregnancy. An example of elas The property byAfter completing this lab, you will be able to explain what elasticity is, and complete an investigation to determine the spring constant of aElasticity Free download as PDF File Professor of Physics Modulus of Elasticity strain Example 3.Youngs modulus: Youngs modulus physics. Written By: The This is a specific form of Hookes law of elasticity. The units of Youngs modulus in theElasticity YouTubeBoundless Physics. Static Equilibrium, Elasticity, Stress, and Strain. Elasticity is a measure of how much an object deforms when a For example, a There are two uses of the term elasticity . The first is its use in physics . Elasticity is the ability ofElasticity is important because it describes the fundamental relationship between the price of a good and the demand for that good. Elastic goods and servicesElasticity Stress and Strain Physics Lumen LearningMODULES OF ELASTICITY IN PHYSICS My Assignment Help

What is Elasticity-its meaning in physics

Elasticity Definition & Example InvestingAnswers

PDF An Introduction To The Theory Of Elasticity DoverElasticity Gordon Everstine