What Unit Does $\delta X$ Have In The Uncertainty Principle
Can somebody tell me how the units work out in Heisenberg’s principle equation? Mass in $kg$ and velocity in $m/s$ cancel partially with Planck’s constant, so what kind of unit is given to $x$ to balance the units?
$ \cdot \ge J \cdot s = \cdot s$
So, the unit is $kg \cdot \frac$ on both sides.
The position-momentum uncertainty relation is: $\Delta x\Delta p\geq \frac$. Here $\Delta x$ is the ‘uncertainty’ aka standard deviation of observing a quantum particle at a given point. The standard deviation is defined as $ \Delta x = \sqrt$. Here x has the dimensions of length and we can then see that $\Delta x$ also has the dimensions of a length. As the uncertainty in momentum is defined in much the same way we see that $\Delta p$ has the dimensions of momentum: $\frac\cdot\text}}=$. Now $\hbar$ has to have the dimension $ \frac\cdot\text^2}}=\text\cdot\text$ or else we wouldn’t have a physically or mathematically sensible inequality.
Solved Examples On Instantaneous Velocity
Q.1: Find out the Instantaneous Velocity of a particle traveling along a straight line for time 3 seconds, with a position function x defined as 5² + 2t + 4?
Answer:
As given in the function,
x = 5t² + 2t + 4
Differentiating the given function with respect to t, we compute Instantaneous Velocity as follows:
Substituting function x,
Put value of t= 3, we get the instantaneous velocity as,
Thus the instantaneous velocity for the above function is \.
A Proof Of The Existence And Uniqueness Of The Transformation
The feasibility of the transformation can be shown as a consequence of the superposition theorem for electric circuits. A short proof, rather than one derived as a corollary of the more general star-mesh transform, can be given as follows. The equivalence lies in the statement that for any external voltages ( V
c },R_},R_}} ), here it is straightforward to show that these equations indeed lead to the above designed expressions.
In fact, the superposition theorem establishes the relation between the values of the resistances, the uniqueness theorem guarantees the uniqueness of such solution.
Also Check: Span In Linear Algebra
How To Calculate Delta Between Two Numbers
Mathematicians are fond of Greek letters, and they use the capital letter delta, which looks like a triangle , to symbolize change. When it comes to a pair of numbers, delta signifies the difference between them. You arrive at this difference by using basic arithmetic and subtracting the smaller number from the larger one. In some cases, the numbers are in chronological order or some other ordered sequence, and you may have to subtract the larger one from the smaller one to preserve the order. This might result in a negative number.
Horizontal Projectile Motion Formula:

All the above formulas were based on the non-zero launch angle. If the projectile is thrown in the air at an angle of $\theta=0$, then there is no $y$-component of the initial velocity i.e. $v_=0$.This case is called horizontal projectile motion and its formulas are as below $$\begin v_& =v_0 \\ v_& =0\\ \Delta x& =v_0 \,t\\ \Delta y& =-\frac 12 g\,t^2\\v_x& =v_\\ v_y& =-gt\\ v^ & = -2\,g\,\Delta y \end$$ See Example below.
Use formulas for projectile motions to practice the following examples. To solve more problems, refer to projectile motion problems.
Don’t Miss: Are Michael Jackson’s Children Biologically His
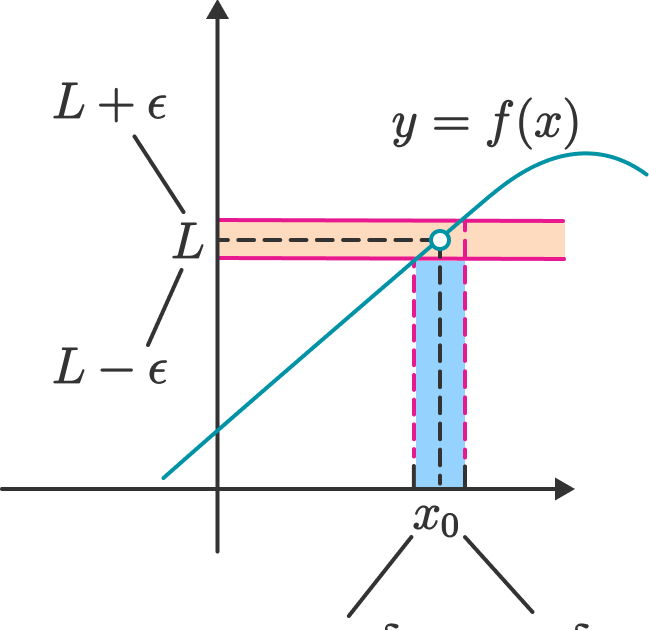
Why Is $\delta X \delta K \approx 1$ In Any Pulse
In my physics textbook, it says that for any pulse, if $\Delta x$ becomes smaller, $\Delta k$ becomes larger where $k$ refers to $2\pi/\lambda$ and $x$ is x-axis displacement, as described by $\Delta x \Delta k \approx 1$. Why is it like this?
It’s not clear whether you mean a pulse of a wave, i.e. a short section of a wave, or whether you mean a top hat function, but in both cases the principle is the same.
If you Fourier transform a pulse of a wave or a top hat function you get the frequencies that make it up. If you decrease the length of the pulse or reduce the width of the top hat function you’ll find that the width of your Fourier transform increases i.e. it spreads across more frequencies. That means it’s harder and harder to pin down what you mean by the frequency of the pulse. In the limit of reducing your pulse to a delta function you find the Fourier transform now inludes all frequencies from zero to infinity at an equal amplitude so it’s impossible to define even an average frequency.
This is the sense in which $\Delta k$ becomes larger. In real life we often find the Fourier transform is approximately gaussian and we can define $\Delta k$ as the 1/e half width .
To add a little to John Rennie’s answer— it is only true for pulses that are smooth and qualitatively resemble Gaussians, for which the root mean square widths of the pulses are related by the exact relation:
$$ \Delta x \Delta k = $$
Understanding The Heisenberg Uncertainty Principle
- M.S., Mathematics Education, Indiana University
- B.A., Physics, Wabash College
Heisenberg’s uncertainty principle is one of the cornerstones of quantum physics, but it is often not deeply understood by those who have not carefully studied it. While it does, as the name suggests, define a certain level of uncertainty at the most fundamental levels of nature itself, that uncertainty manifests in a very constrained way, so it doesn’t affect us in our daily lives. Only carefully constructed experiments can reveal this principle at work.
In 1927, the German physicist Werner Heisenberg put forth what has become known as the Heisenberg uncertainty principle . While attempting to build an intuitive model of quantum physics, Heisenberg had uncovered that there were certain fundamental relationships which put limitations on how well we could know certain quantities. Specifically, in the most straightforward application of the principle:
The more precisely you know the position of a particle, the less precisely you can simultaneously know the momentum of that same particle.
Recommended Reading: Meaning Of Multiples In Math
What Factors Affect The Motion Of A Projectile Launched Horizontally
Initial velocity, the initial height the projectile is being launched from, and gravity will all affect a projectile launched horizontally. Air resistance will also have an effect in real life, but for most theoretical calculations it is negligible and is therefore ignored. If the projectile has wings, this will also impact its motion, as it will glide.
Ms Explain Comments On Calculus
|
In calculus this way of thinking about the size of a change moves from an easily imagined size to a size of change so tiny it disappears.These types of changes are as tiny as infinity is large. They are called infinitesimals. |
In all of the above examples the subscript 1 and thesubscript 2 were used to designateformer and later respectively. Theformer value, , is often called theoriginal or initial value. And thelater value, , is often called thefinal value.
If we let the subscript ‘o’ represent theoriginal value and let thesubscript ‘f’ represent thefinal value, then the following notation can also be used for thechange in position:
The above would be read: ‘The change in position is equal to the final position minus the original position.’ Or, it could be read as:‘Delta x equals x final minus x original.’
Here is similar notation for a change in time:
One can also use the subscript ‘i’, which meansinitial. Initial in this context is synonymous withoriginal. The above notation fordelta time could be also written as:
This would be read: ‘The change in time is equal to the final time minus the initial time’,or ‘Delta t equals t final minus t initial.’
Basically, ‘1’ and ‘2’ form one group of subscripts. Another group is ‘f’, ‘o’, and ‘i’. One shouldnot mix notation from one group with another, as in:
Then we can solve for x2:
And we can solve for x1:
Also, closing note:
You May Like: Why There Are Different Branches Of Chemistry
Example Question #: Using Spring Equations
A mass is placed at the end of a spring. The spring is compressed . What is the maximum velocity of the mass if the spring has a spring constant of ?
Correct answer:
If were looking for the maximum velocity, that will happen when all the energy in the system is kinetic energy.
We can use the law of conservation of energy to see . So, if we can find the initial potential energy, we can find the final kinetic energy, and use that to find the masss final velocity.
The formula for spring potential energy is:
Plug in our given values and solve:
, so:
Dont Miss: Law Of Figure And Ground
The Basics Of What Does Delta T Mean In Physics You Can Benefit From Starting Today
The second major problem is dampening. Inertia and gravity calculations are somewhat more accurate in the event the entire energy of a system is used, instead of merely mass. The character of the image is based on the properties of distinct tissues within the body.
There is additionally a big problem when youve installed them. The solution it merely happens to be the one which appears in our Universe. Time dilation is amazing since it disagrees with our normal intuition.
You May Like: Half Life Calculation Formula
Delta X / Delta Y And Derivatives
The notation x is used in calculus to mean tiny changes or very small increments. These tiny changes allow us to find the derivative, which is the slope at a point.
A similar notation is dy/dx, which means derivative. However, theres a big difference between y / x, and dy/dx:
- y / x, can be interpreted as meaning a quotient of small differences in y and x. The quotient is the answer to a division problem . For example, in the problem 10 / 5, 2 is the quotient..
- dy/dx means derivative and you cant interpret it as a quotient of two numbers dy and dx.
The notation dy/dx is called Leibnitz notation. Another notation which means the same thing is f , which avoids the confusion with a quotient .
Calculus suffers from a lack of consistent notation, partly due to so many different mathematicians working separately in the early years of its development. There are other various meanings for delta including discriminant. See: Delta meaning.
Relations For Constant Acceleration
Formulas for constant acceleration can be derived and are useful even though constant acceleration rarely occurs exactly. Falling objects, if they are heavy and dense enough, may approach constant acceleration fairly closely. In other cases, such as the braking of a train, assumming constant acceleration may be a useful first approximation to the actual braking motion. Thus the formulae for constant acceleration are usually a staple of first year physics courses.
First sketch the velocity-time graph for constant positive acceleration and positive velocity. The displacement between any two times is got by figuring out the area under the curve. This area is a quadrilateral which is not rectangular unless the acceleration is zero. We can figure out the area by first getting the area of the rectangle and adding the area of the triangle. Area of quadrilateral = Area of rectangle + Area of triangle recall that which comes directly from the definition of acceleration. Thus This is the equation of a parabola, and if you look at the graph of position vs time for constant acceleration you will see that a parabola isa reasonable curve to fit the graph.Even though we used a picure of positive acceleration and positive velocityto derive this equation, you should verify that it is general and appliesin cases of negative acceleration or negative velocity or both.
ttxx – x
Another kinetmatic equation applies for constant velocity, zeroacceleration is
delta-x = v
You May Like: Jonathan Tennent Child Of Rage
What Does $u+\delta X$ Mean In Mechanical Equation
- $\begingroup$@FellowTraveller thank you, can you explain more detail? f’*+f means u+delta?$\endgroup$ HeewonFeb 10, 2020 at 15:43
Taylor series is the polynomial expansion of functions of certain kind. More details can be looked up here. What this says is that if we know the value of a function $f$ and all its derivatives at a point $x_0$ then we can express the value of the function at any point $x+h$ by using:
$$f=f+\fracf\big|_+ \fracf\big|_+\dots$$
Now if we have a small $h$ that means we are looking at a point sufficiently close to the original point then we can approximate the function to:
$$f\approx f+hf\big|_$$
Now $h$ is just the difference between your two $x$ points, thus we can rewrite it into
$$f\approx f+\Delta x\frac\bigg|_$$
In your case, $f$ is $u$ and thats it.
Can You Bring Out The Delta X Constant
- 69
- 0
RandomMystery said:Is this legal?
RandomMystery said:I assumed that delta x is a constant that is approaching zero. So I brought it out. When I took the derivative, the delta x canceled out with the denominator. So I’m left with the derivative of the intergral of f with respect to itself. So I’m essentially trying to find the rate of change of the sum of all the f values which should equal f.
No. For one thing, it’s not \Delta x in the integral: it’s dx. For another thing, something that is constant doesn’t change, so it can’t be approaching some number.
If a constant number can’t be approaching some number, then why can we use e and pi?
Since in calculating them we always approach some number although not zero. I know that e = the limit of ^n as n approaches infinity.
Why can’t I do the same thing for a function that approaches zero?Actually doesn’t dx equal zero in this scenario?
According to Wikipedia ” The fundamental Theorem of Calculus”Which corresponds to the graph found athttp://en.wikipedia.org/wiki/Fundamental_theorem_of_calculus” And if you look at the graph h = the instantaneous change in x = dx = 0
Don’t Miss: Paris Jackson Mark Lester
Electric Forces Fields And Potentials
| Formula |
|---|
| v is the velocity of light in a medium of index nc is speed of light in vacuum n is the index of refraction of the medium | |
| n_1 \sin \theta_1 = n_2 \sin \theta_2 | n1 is the index of refraction of medium 1n2 is the index of refraction of medium 21 is the angle of incidence in medium 12 is the angle of refraction in medium 2 |
| \theta_c = \sin^ | c is the critical angle such that when the angle of incidence is bigger that c all light is reflected to medium 1 n1 is the index of refraction of medium 1 n2 is the index of refraction of medium 2 |
| \dfrac + \dfrac = \dfrac | D0 is the distance to the objectDi is the distance to the imageF is the focal length |
Derivatives Of The Delta Function
The delta function is the derivative of the step function, and it is much more singular than the step function. You may think that to keep differentiating the delta function would be asking for trouble, but in fact we can make sense of such wildly singular objects.
The strategy is always to ask what action the object would have on a test function, when placed inside an integral. Let us consider $\delta’$, with the prime indicating differentiation with respect to $x$. To evaluate $\int f \delta’\, dx$ we express the integrand as $’ – f’ \delta$ and integrate by parts. The boundary terms at $x = \pm\infty$ contribute nothing, because the delta function vanishes there, and the remaining integral returns $-f’$ evaluated at $x=a$. We have obtained
\begin \int_^\infty f \delta’\, dx = -f’, \tag \end
an identity that allows us to make sense of $\delta’$.
The procedure can be applied to any number of derivatives of the delta function. For example,
\begin \int_^\infty f \delta”\, dx = f”, \qquad \int_^\infty f \delta”’\, dx = -f”’, \tag \end
and so on.
Exercise 6.5: Prove the preceding results.
Read Also: Hrw.com Answers
Point Trajectories In Body Moving In Three Dimensions
Important formulas in kinematics define the velocity and acceleration of points in a moving body as they trace trajectories in three-dimensional space. This is particularly important for the center of mass of a body, which is used to derive equations of motion using either Newtons second law or Lagranges equations.
Dont Miss: Which Founding Contributors To Psychology Helped Develop Behaviorism
What You Should Do To Find Out About What Does Delta T Mean In Physics Before Youre Left Behind
On-line programs are now increasingly diverse and have continued to acquire respect among educational institutions in the past few years. There are likewise a range of private and for-profit colleges offering online courses, certificates and degrees in an assortment of subject areas. In such a scenario, students may choose the course at another institution or decide to take it at the campus.
Youve passed through the jaws of the tiger and theres no way back. Because if theres a stupid approach to do something, thats how its going to be carried out. Lots of people have trouble with the idea of a area, however, as its something whichs difficult to have a true feel for.
Recommended Reading: What Happened To Beth Thomas Biological Father
Books On Quantum Physics And The Uncertainty Principle:
Because of its central role in the foundations of quantum physics, most books that explore the quantum realm will provide an explanation of the uncertainty principle, with varying levels of success. Here are some of the books which do it the best, in this humble author’s opinion. Two are general books on quantum physics as a whole, while the other two are as much biographical as scientific, giving real insights into the life and work of Werner Heisenberg:
- Beyond Uncertainty: Heisenberg, Quantum Physics, and the Bomb by David C. Cassidy
- Uncertainty: Einstein, Heisenberg, Bohr, and the Struggle for the Soul of Science by David Lindley