introduction To Scaling Laws
There are many different scaling laws. At one extreme, there aresimple scaling laws that are easy to learn, easy to use, and veryuseful in everyday life. Scaling laws can be and should be introducedat the elementary-school level, and then reinforced and extended everyyear through middle school, high school, and beyond. Scaling laws arecentral to physics. This has been true since Day One of modernscience. Galileo presented several important scaling results in 1638.
This document is meant to be a tutorial, covering the simplest andmost broadly useful scaling laws.
At the other extreme, there are more subtle scaling laws that are usedto solve very deep and complicated problems at the frontiers ofscientific research. The importance of scaling continues to thepresent day. There are dozens of references to & #X201C scaling& #X201D at theNobel Prize site .
& #XA0 Don& #X2019 t let this scare you away. To repeat: this document is meant to be atutorial, covering the simplest and most broadly useful scaling laws.You don& #X2019 t need to be a Nobel laureate to get a lot of value fromscaling laws.
You may be familiar with a simple form of scaling in connection withscale models, such as in figure& #XA0 1 and figure& #XA0 2. The same word shows up in connection withsmall-scale and large-scale maps. For more about the terminology,see section& #XA0 3.
What’s The Use Of The ‘fn’ Key In The Keyboard
Fn is short for Function and is a key found on most laptop keyboards and some desktop keyboards. The Fn key performs special functions, such as adjusting screen brightness and speaker volume. Most computer keyboards use the Fn key like other modifier keys . Holding down the Fn key along with another Fn key performs this function.
example: Reflection From A Change In Refractive Index
Suppose a wave encounters the interface between one mediumand another medium with a slightly different index of refraction.There will always2 be somereflection from such an interface. The amount of reflection dependson the angle, and on the change in index, in accordance with theFresnelequations.
Let the relative change in index be called & #X454 . That is,n2 / n1 = 1 + & #X454 , for some small & #X454 . It may behelpful to think of & #X454 in terms of the logarithmic derivative:& #X454 = & #X394 ).
You can show that at any particular angle, the amount of reflectionscales like & #X454 squared. This is a famous result, worthremembering. Perhaps more importantly, you don& #X2019 t need to remember it,because you can rederive it whenever you need it, just by looking atthe structure of the Fresnel equations. Expand the RHS as a Taylorseries in & #X454 . The zeroth-order term is zero, the first-orderterm is zero, and the second-order term is nonzero. This is an easyexercise in theoretical physics, involving little more thandifferentiating a polynomial. The coefficients of the polynomial arecomplicated functions of & #X3B8 , but still it& #X2019 s just a polynomialfunction of & #X454 . It& #X2019 s even simpler as a function of n, anddn/d& #X454 = 1, so it comes to the same thing either way.
We say that there is a universality property here. There is auniversal curve for & #X454 2Rp, independentof & #X454 , when & #X454 is small.
You May Like: How Do Noise Cancelling Headphones Work Physics
Where Is The Fn Key On A Macbook
On MacBook laptops, the Fn key is located at the bottom left of the keyboard. On all Apple computers running macOS, the F1 F12 function keys perform their special standard functions, such as adjusting brightness or volume. When the Fn key is pressed, the F1 F12 keys perform an application-specific action.
Quantum Physics And Decoherence

Outside of highly controlled laboratory conditions, quantumsystems are in constant interaction with the environment. These countlessinteractions include air molecules, thermal radiation, and cosmic radiation. Theinitial theoretical development of quantum physics focused on isolated systemsand did not consider the implications of the interactions with the environmentin open systems.
These countless interactions are actually the environmentbecoming entangled with which-path information for a quantum system. Although the amount of which-path informationin each individual interaction is tiny, the cumulative effect of all theinteractions is decisive. Substantial theoretical and experimental researchconfirms this conclusion . As noted inthe previous section, which-path entanglement results in the loss of quantumsuperpositions and causes the quantum-to-classical transition.
These environmental interactions cause the absence ofquantum effects in our everyday world . The elimination of quantum superpositions by environmental interactionsis called . For example, estimates of decoherence times for adust grain are so fast that superpositions would be extremely difficult toobserve . The decoherence times forlarger objects are many orders of magnitude faster.
Don’t Miss: Holt Geometry Answers
Why Is The Backspace Not Working On My Keyboard
The backspace key does not work on the keyboard. Solution 1: Disable Sticky Keys and Filter Keys. Sticky Keys and Filter Keys are two ways to access it. Solution 2. Reinstall your keyboard. Lost communication between the keyboard and the Windows operating system. Solution 3: Update your keyboard driver. The above solutions may solve your problem, but if not, then you need to upgrade.
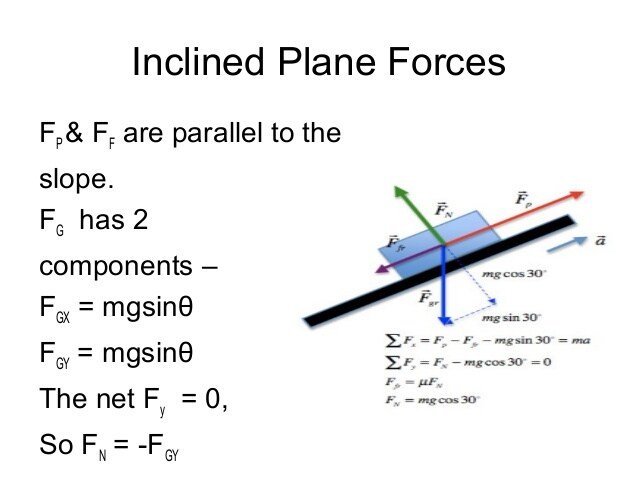
Concept Of Normal Force:
The normal force is thoroughly defined as the force component vertical to any contact surface. It also decides the amount of force which the body applies on the ground.
The normal force will be equivalent to the weight of the object only if the object is not accelerating i.e. decelerating. When an object is about to fall, then it will depend on which position the object falls on the ground. It is denoted by \ and is given in newton .
Don’t Miss: What Happened To Beth Thomas Biological Father
Potential Outcomes And Imagination
The terms in the quantum wave function symbolize potentialoutcomes similar to the human imagination of potential future events. Bothinvolve symbols of potential conditions rather than symbols of existing tangiblereality. In both cases, the manifestation of one of the potential outcomes canbe viewed as information creation. However, the concepts of media andinterpretational infrastructure are clearly applicable for human imagination,but are of doubtful applicability for quantum processes.
Awesome Example: The Rule Of 72
The Rule of 72 is a mental math shortcut to estimate the time needed to double your money. Were going to derive it and even better, were going to understand it intuitively.
How long does it take to double your money at 100% interest, compounded every year?
Uh oh. Weve been using natural log for continuous rates, but now youre asking for yearly interest? Wont this mess up our formula? Yes, it will, but at reasonable interest rates like 5%, 6% or even 15%, there isnt much difference between yearly compounded and fully continuous interest. So the rough formula works, uh, roughly and well pretend were getting fully continuous interest.
Now the question is easy: How long to double at 100% interest? ln = .693. It takes .693 units of time to double your money with continuous compounding with a rate of 100%.
Ok, what if our interest isnt 100% What if its 5% or 10%?
Simple. As long as rate * time = .693, well double our money:
- rate * time = .693
- time = .693/rate
So, if we only had 10% growth, itd take .693 / .10 or 6.93 years to double.
To simplify things, lets multiply by 100 so we can talk about 10 rather than .10:
- time to double = 69.3/rate, where rate is assumed to be in percent.
Now the time to double at 5% growth is 69.3/5 or 13.86 years. However, 69.3 isnt the most divisible number. Lets pick a close neighbor, 72, which can be divided by 2, 3, 4, 6, 8 and many more numbers.
- time to double = 72/rate
which is the rule of 72! Easy breezy.
You May Like: My Hrw Com Algebra 1
How To Find Normal Force
wikiHow is a wiki, similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 16 people, some anonymous, worked to edit and improve it over time.There are 11 references cited in this article, which can be found at the bottom of the page. This article has been viewed 722,570 times.Learn more…
Normal force is the amount of force required to counteract the other forces in any given scenario. The best way to go about finding it depends on the circumstances of the object and the variables you have data for. Keep reading to learn more.
What Do You Mean Best Line
Associated with each data point is an error bar, which is thegraphical representation of the uncertainty of the measuredvalue. We assume that the errors are normallydistributed, which means that they are described by thebell-shaped curve or Gaussian shown in the discussion of standard deviation. The heightbetween the data point and the top or bottom of the error bar is, so about 2/3 of the time, the line orcurve should pass within one error bar of the data point.
Sometimes the uncertainty of each data point is the same, but it is just aslikely that the uncertainty varies from datum todatum. In that case the line should pay more attention to the points thathave smaller uncertainty. That is, it should try to get close to those”more certain” points. When it can’t, we should grow worried that the dataand the line fundamentally don’t agree.
A pretty good way to fit straight lines to plotted data is to fiddle with aruler, doing your best to get the line to pass close to as many data pointsas possible, taking care to count more heavily the points with smalleruncertainty. This method is quick and intuitive, and is worth practicing.Here’s my attempt to fit a line by eye.
Recommended Reading: What Is The Formula Of Volume In Physics
Using Natural Logs With Any Rate
Sure, you say, This log stuff works for 100% growth but what about the 5% I normally get?
Its no problem. The time we get back from $\ln$ is actually a combination of rate and time, the x from our $e^x$ equation. We just assume 100% to make it simple, but we can use other numbers.
Suppose we want 30x growth: plug in $\ln$ and get 3.4. This means:
- $e^x = \text$
- $e^ = 30$
And intuitively this equation means 100% return for 3.4 years is 30x growth. We can consider the equation to be:
We can modify rate and time, as long as rate * time = 3.4. For example, suppose we want 30x growth how long do we wait assuming 5% return?
- $\ln = 3.4$
- $\text * \text = 3.4$
- $.05 * \text = 3.4$
- $\text = 3.4 / .05 = 68 \text$
Intuitively, I think “$\ln = 3.4$, so at 100% growth it will take 3.4 years. If I double the rate of growth, I halve the time needed.”
- 100% for 3.4 years = 1.0 * 3.4 = 3.4
- 200% for 1.7 years = 2.0 * 1.7 = 3.4
- 50% for 6.8 years = 0.5 * 6.8 = 3.4
- 5% for 68 years = .05 * 68 = 3.4
Cool, eh? The natural log can be used with any interest rate or time as long as their product is the same. You can wiggle the variables all you want.
Moving Front Of Increasingly Complex Entanglement
The fact that which-path entanglement results in decoherenceof each particle, but superposition of the relationship between particles, demonstratesthat an interaction can cause both superposition of a higher order anddecoherence of a lower order. This point is implied is various writings and wasclearly described by Garret . This shifting of superposition may betypical of interactions and is consistent with the quantum wave function thatpredicts endlessly increasing entanglement, but does not specifically describea collapse of the wave function.
One important question is whether some interactions causesuperpositions to collapse as historically assumed for measurement, or whethera more appropriate model is that superpositions endlessly shift to higher orderinteractionsâwith the classical world emerging behind this moving front ofincreasingly complex entanglement. The latter is more consistent with the wavefunction. Analysis of multiple and sequential interactions may provide insightsabout limitations on higher order entanglement and lower order decoherence, andabout the measurement problem.
Also Check: Physics Finding Acceleration
What Does Function Of Mean
Annotation category:Chapter 3
| Note: |
A function defines one variable in terms of another. The statement “y is a function of x” ) means that y varies according to whatever value x takes on. A causal relationship is often implied , but does not *necessarily* exist.
The number of hours you spend toiling away in Butler library may be a function of the number of classes you’re taking. It’s also likely to be a function of whether you have a computer in your dorm room, whether you have a printer in your dorm room, and whether your roommates are loud and obnoxious and won’t let you study.
In turn, the number of classes you’re taking may be a function of your major. It is also likely to be a function of how many extracurricular activities you participate in, how much sleep you need, and how crazy you are.
Knowing that one variable somehow changes with another is a starting point. Uncovering the specific nature of their relationship is another, and in science it is vital to understanding how systems behave. Such work can become a complicated business. Fortunately we have access to a language which, although it may have earned the undeserved reputation of being hopelessly complex, is actually the simplest, most efficient way to solve these problems. So let’s do some translating:
If y = 2x, that means that for every incremental increase in x, y increases by 2 increments. Y is twice the value of x, for every value x takes on.
If x = 5, then y = 2 x 5 = 10.
so that y = 365x + x/4 + b.
reducing The Number Of Variables
Suppose we want to make a movie of an enormous pendulum clock, and wewant the physics to look correct. The obvious way to do it would beto build a full-sized clock and film it using a normal camera.
However, there is another way to do it. We could build a scale-modelclock, and then film it in slow motion. In other words, we modifyboth the length-scale and the time-scale. If we do this correctly,the result looks entirely natural. Specifically, the scale-factorapplied to the time must be the square root of the scale-factorapplied to the length, as mentioned in item 8.
Let us focus on the specific question of whether the behavior willlook correct. To answer this question, at first glance it seems weneed to know two things, namely the time-scale and thelength-scale . However, because there exists a scaling law, wereally only need to know one thing, namely the ratio t/& #X221A L.
As a more extreme example, consider the question of whether the flowpast a sphere will be turbulent. To answer this question, at firstglance it seems we need to know four things, namely the speed ,the size , the fluid density , and the viscosity .However, because there exists a scaling law, we really only need toknow one thing, namely the Reynolds number, i.e. the ratio& #X3C1 VL/& #XB5 , as mentioned in item 32.
You May Like: Who Are Paris Jackson’s Biological Parents
What Is Periodic Function
A body is said to be in periodic motion if the motion its executing is repeated after equal intervals of time, like a rocking chair, a swing in motion. A periodic function can be defined as:
A function returning to the same value at regular intervals.
Though periodic motion and oscillatory motion sound the same, not all periodic motions will be oscillatory motion. The major difference between a periodic motion and oscillatory motion is that periodic motion is relevant to any motion that repeats over time, but the oscillatory motion is unique to those motions that execute about an equilibrium point or between two states. A periodic function can define all periodic motions.
Periodic function of a pendulum bob
To understand the concept of periodic function lets consider a pendulum bob, oscillating along with its equilibrium position, the trajectory of the bob is shown below, now if the bob is oscillating then, its displacement will also vary from zero to positive and back to zero and negative, this can be easily illustrated with a graph,
Periodic Function
What Is The The F Keys Do On The Keyboard
What are the function keys F1 to F12 used for on the F1 keyboard? The F1 key is ubiquitous in almost every program, be it Chrome or Microsoft Word. The F2 key. Shortcut to rename any of the selected icons, files or folders. The F3 key. The F4 key. The F5 key. The F6 key. The F7 key. The F8 key. The F9 key. The F10 key.
Read Also: Psychology Figure Ground
example: Equilibrium And Activity
9.3.1& #XA0 & #XA0 Introduction
Let& #X2019 s consider the ultra-simple chemical reaction
| F2& #XA0 & #X2194 & #XA0 2F& #XA0 & #XA0 & #XA0 & #XA0 & #XA0 & #XA0 & #XA0 & #XA0 & #XA0 & #XA0 & #XA0 & #XA0 & #XA0 |
and in particular let& #X2019 s consider the equilibrium state in a vesselwhere that reaction is occurring in the gas phase. Let X denote thereaction coordinate, i.e. the degree to which the reaction hasproceeded toward the right. Specifically, X=0 if we have 100%& #X201C reactants& #X201D , and X=1 if we have 100%& #X201C products& #X201D .
We choose conditions of temperature and molar volume such that X isinitially small but nonzero. We hold the temperature constant, andincrease the system volume V by moving a piston. We predict thatincreasing the volume by a factor of Q increases X by a factor of& #X221A Q.
Let& #X2019 s work out the numbers for a simple scenario. We adopt theconvention that in this context , squarebrackets denote number density, i.e. the reciprocal of themolar volume. This is the convention used in introductory-levelchemistry courses and in many advanced, practical applications.
| & #X2014 & #X2014 & #XA0 A& #XA0 & #X2014 & #X2014 |
| & #X2192 |
| 2 |
| 2 |
| 2 |
As the final step, we allow the chemical reaction to come toequilibrium under the new conditions. The number density of unboundF atoms will increase.
Another thing you can see is that the ratio in the bottom row isthe same in both equilibrium situations. This leads us to define
| Kd& #XA0 :=& #XA0 |
Here are the main points:
| & #X2212 E |
| kT |