Everyday Usage And Application Of Exponents
Although you don’t often run across the need to multiply a number by itself a certain amount of times, there are many everyday exponents, especially in units of measurement like square and cubic feet and inches, which technically mean “one foot multiplied by one foot.”
Exponents are also extremely useful in denoting extremely large or small quantities and measurements like nanometers, which is 10-9 meters, which can also be written as a decimal point followed by eight zeros, then a one . Mostly, though, average people don’t use exponents except when it comes to careers in finance, computer engineering and programming, science, and accounting.
Exponential growth in itself is a critically important aspect of not only the stock market world but also of biological functions, resource acquisition, electronic computations, and demographics research while exponential decay is commonly used in sound and lighting design, radioactive waste and other dangerous chemicals, and ecological research involving decreasing populations.
What Is An Exponent In Mathexponents Examples
What is an exponent? An exponent is something that tells you how many times to multiply a number by itself in a sum. An exponent can also be called an index or a power. Exponents are placed to the top right of a base number. This base number is the number being multiplied by itself a certain amount of times.
What Is An Exponent In Math Your Guide
Lets get straight to your question: What is an exponent in math? Well, its the repeated multiplication of a specific number by itself. The number of times this value is multiplied by itself is indicated by the value of the exponent.
Let’s define exponents and explore the basic rules of exponentiation, which is the process of raising one quantity to the power of another.
You May Like: Geometry Segment Addition Postulate Worksheet
How To Write A Number In Exponential Form
As we discussed earlier that it is nothing but simply to express a numerical term raised to certain powers of its prime factors based on the following way:
Base Exponent
Therefore, to express a number in exponential form the very first step is to write the number as the product of its prime factors.
Let us take the example of the number 1260.
When we express 1260 as a product of its prime factors then we can write it as
1260= 2x2x3x3x5x7
However, in the exponential form, the same number can be:
1260= 22 x 32 x51 x71
Therefore, we can see that expressing a number in its exponential form can be an easier task and it also saves time and space while writing.
Therefore we may conclude that whole numbers can be expressed in exponential form by raising the powers of their prime factors in which the exponent helps in telling us that how many times the base has been used as a factor.
Powers / Exponents Of 10
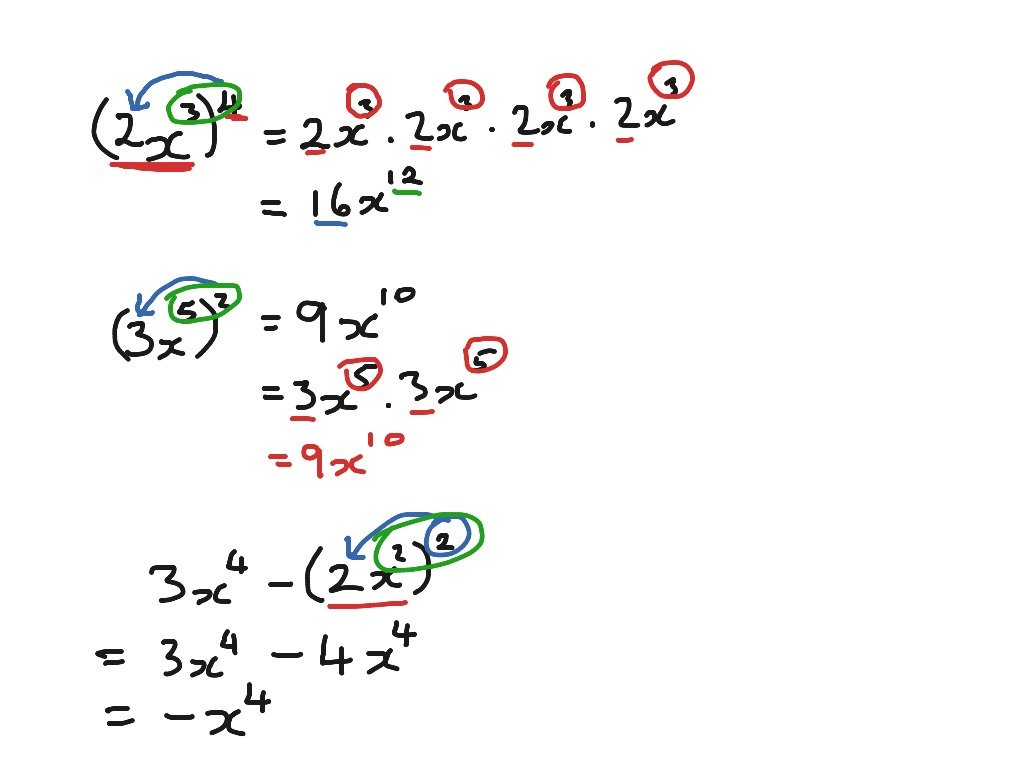
Exponents examples involving 10 as the base number crop up fairly frequently in Math and other Scientific subjects. Where 10 is multiplied by itself a number of times. It works out that a positive exponent number of 10 , in fact tells us how many 0 ‘s come after the 1 in the whole number result.
1010
Don’t Miss: Segment Addition Postulate Find The Length Indicated
What Are The Real
Exponents have various applications. Few exponents applications are listed below:
- Exponents are widely used in computer games, measuring scales.
- Scientific scales like the pH scale or the Richter scale are based on exponents.
- Exponents are used while calculating the area, volume, and problems related to measurement.
- Exponents are most commonly used in the respective field of Science, Engineering, Economics, Accounting, Finance.
- Exponents are often used to represent a computer’s or laptop’s memory.
Properties Of Exponents And Scientific Notation
- Publisher: OpenStax CNX
- Simplify expressions using the properties for exponents
- Use the definition of a negative exponent
- Use scientific notation
Before you get started, take this readiness quiz.
Read Also: Intermediate Algebra Final Exam Practice
What Is Exponential Function In Your Own Words
In mathematics, the exponential function is the function e, where e is the number such that the function e is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change in the dependent variable.
Exponents In Finances Marketing And Sales
Exponents are especially important in calculating compound interest because the amount of money that is earned and compounded depends on the exponent of time. In other words, interest accrues in such a way that each time it is compounded, the total interest increases exponentially.
Retirement funds, long-term investments, property ownership, and even credit card debt all rely on this compound interest equation to define how much money is made over a certain amount of time.
Similarly, trends in sales and marketing tend to follow exponential patterns. Take for instance the smartphone boom that started somewhere around 2008: At first, very few people had smartphones, but over the course of the next five years, the number of people who purchased them annually increased exponentially.
Recommended Reading: Theory Of Everything 2 Geometry Dash
What Is An Exponent
Exponentiation is a mathematical operation, written as an, involving the base a and an exponent n. In the case where n is a positive integer, exponentiation corresponds to repeated multiplication of the base, n times.
an = a × a × … × a n times
The calculator above accepts negative bases, but does not compute imaginary numbers. It also does not accept fractions, but can be used to compute fractional exponents, as long as the exponents are input in their decimal form.
Math : What Is An Exponent And How Do You Solve It
While studying for the math section, you may have heard of an exponent as something to the power of. For example, in the expression 42 the problem is asking you to find 4 to the 2nd power.
Power refers to the number of times you multiply, not what Superman uses to fight off villains.
Tumblr
So whats the difference between exponents and regular multiplication?
Recommended Reading: Define Movement In Geography
How Do Exponents Relate To Real Life
In real life, we use the concept of exponents to write numbers in a simplified manner and in a short way. Repeated multiplication can be easily written with the help of exponents. Also, we use exponents to write larger numbers, for example, the distance of the moon from earth, the number of bacteria present on a surface, etc.
What Is An Exponent In Math

Exponents are usually written in superscript, which is when a small number is placed above and to the right of the base:
The base number x represents the value that is being multiplied by itself. The value of n is the exponent, which represents the number of times the base number will be multiplied by itself. In short, x will always be multiplied by itself n times.
Read Also: Geometry Segment Addition Postulate Worksheet
What Is The Meaning Of Base And Exponent In Math
4.5/5baseexponentbaseexponentbasebaseseen here
In mathematics, a base or radix is the number of different digits or combination of digits and letters that a system of counting uses to represent numbers. For example, the most common base used today is the decimal system. Because “dec” means 10, it uses the 10 digits from 0 to 9.
Secondly, what is the base of the exponent? An expression that represents repeated multiplication of the same factor is called a power. The number 5 is called the base, and the number 2 is called the exponent. The exponent corresponds to the number of times the base is used as a factor.
Simply so, what is the meaning of exponent in math?
An exponent refers to the number of times a number is multiplied by itself. For example, 2 to the 3rd means: 2 x 2 x 2 = 8. 23 is not the same as 2 x 3 = 6. Remember that a number raised to the power of 1 is itself.
What is meant by base?
In chemistry, a base is a chemical species that donates electrons, accepts protons, or releases hydroxide ions in aqueous solution. Types of bases include Arrhenius base, Bronsted-Lowry base, and Lewis base.
The general steps for converting a base 10 or “normal” number into another base are:
Questions To Be Solved:
Question 1) Find the value of the 25.
Solution) To find the value of 25We need to multiply the base that is equal to 2 , and the exponent tells us how many times the number needs to be multiplied by itself.
25 = 2 × 2 × 2 × 2 × 2 equals 32.
Question 1)What is an Exponent and What is Power in Math?
Answer) Lets know about exponent and power.An expression that represents repeated multiplication of the same factor is known as a power. For example, 52 here, the number 5 is known as the base, and the number 2 is known as the exponent. The exponent is 2 that correspond to the number of times the base is used as a factor.
Question 2) What is Power in Math?
Answer) The power of a number basically defines how many times to use the number in the multiplication process. It is written as a small number to the right and above the base number whose power we need to find.
Question 3) What are the 7 Laws of Exponents?
Answer)Here are the seven laws of exponents :
-
Multiplying the powers that have the same Base.
-
Dividing Powers having the same Base.
-
Power of a Power.
-
Multiplying Powers that have the same Exponents.
-
The concept of Negative Exponents.
-
Power with Exponent equal to Zero.
-
Fractional Exponent.
You May Like: Segment And Angle Addition Postulate Worksheet Answers
Efficient Computation With Integer Exponents
Computing bn using iterated multiplication requires n 1 multiplication operations, but it can be computed more efficiently than that, as illustrated by the following example. To compute 2100, apply Horner’s rule to the exponent 100 written in binary:
- 100
by using exponentiation by squaring, where n denotes the number of 1 in the binary representation of n. For some exponents , the number of multiplications can be further reduced by computing and using the minimal addition-chain exponentiation. Finding the minimal sequence of multiplications for bn is a difficult problem, for which no efficient algorithms are currently known , but many reasonably efficient heuristic algorithms are available. However, in practical computations, exponentiation by squaring is efficient enough, and much more easy to implement.
What Is The Use Of The Properties Of Exponents
There is a major use of properties of exponents in mathematics, especially in algebra. With the help of properties of exponents, we can easily simplify the expressions and also write the expressions in fewer steps. Let us understand this with a simple example. With the help of exponents properties, 24× 26 can be simplified in two quick steps as 24× 26 = 2 = 210.
You May Like: Practice 2-4 Reasoning In Algebra Answers
Basic Exponent Laws And Rules
When exponents that share the same base are multiplied, the exponents are added.
an× am = aEX:22× 24 = 4 × 16 = 64 22× 24 = 2 = 26 = 64
When an exponent is negative, the negative sign is removed by reciprocating the base and raising it to the positive exponent.
| a = |
| EX: 2 = 1 ÷ 2 ÷ 2 ÷ 2 | = |
When exponents that share the same base are divided, the exponents are subtracted.
| am |
When exponents are raised to another exponent, the exponents are multiplied.
n = a4 = 2 = 28 = 256
When multiplied bases are raised to an exponent, the exponent is distributed to both bases.
n = an× bnEX: 2 = 82 = 642 = 22× 42 = 4 × 16 = 64
Similarly, when divided bases are raised to an exponent, the exponent is distributed to both bases.
| ( |
When an exponent is 1, the base remains the same.
a1 = a
When an exponent is 0, the result of the exponentiation of any base will always be 1, although somedebate surrounds 00 being 1 or undefined. For many applications, defining 00 as 1 is convenient.
a0 = 1
Shown below is an example of an argument for a0=1 using one of the previously mentioned exponent laws.
If an× am = aThenan× a0 = a = an
Thus, the only way for an to remain unchanged by multiplication, and this exponent law to remain true, is for a0 to be 1.
What Are Exponents In Algebra
An exponent is a number that is placed as a superscript over a number. In other words, it indicates that the base is raised to a certain power. The exponent is also called by other names like index and power.If m is a positive number and n is its exponent, then mn means m is multiplied by itself for n times.
Also Check: Exponent Rules Worksheet Answer Key
What Is Exponential Function
An exponential function is a Mathematical function in form f = ax, where x is a variable and a is a constant which is called the base of the function and it should be greater than 0. The most commonly used exponential function base is the transcendental number e, which is approximately equal to 2.71828.
Difference Between Power And Exponent With Example
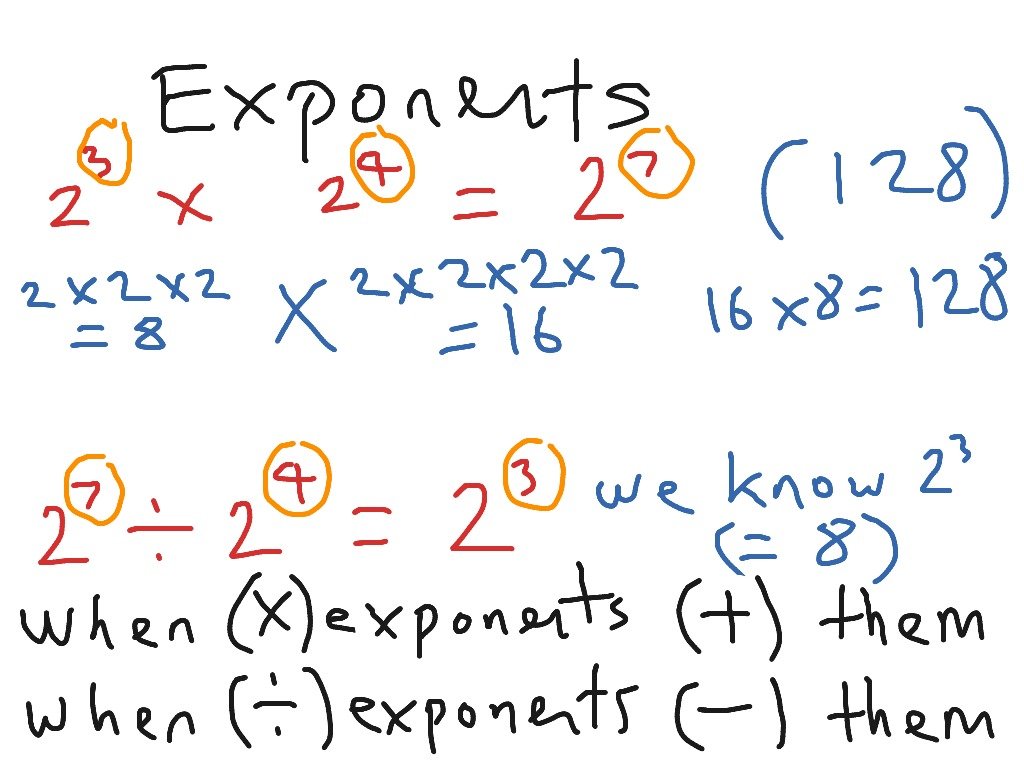
Lets list down the difference between exponent and power with example.
Definition:
In mathematical relationships, power is referred to the number of times a number is multiplied by itself meaning the number you get raising a number to an exponent whereas an exponent can be defined as the number of times the number is used in a multiplication.
Exponents are often known as powers or indices. In simple terms, power can be defined as an expression that represents repeated multiplication of the same number whereas exponent is the quantity that represents the power to which the number is raised. Both these terms are often used interchangeably in mathematical operations.
Example of Power and Exponent:
The expression 5 × 5 × 5 can always be written in a shorter way as 53 using the concept of exponents, 5 × 5 × 5 = 53.The expression basically represents repeated multiplication of the same number which is known as power. Here the number 5 represents the base and the number 3 represents the exponent and the whole expression denotes that 5 to the power of 3 or 5 to the third power which means that over here 5 is multiplied by itself three times.
Similarly, 25 = 2 × 2 × 2 × 2 × 2 is equal to 32.The expression basically denotes 2 to the power of 5 or 2 to the 5th power. In Mathematics, exponents make it easy to write and use multiplications factor.
Also Check: Who Is Generally Recognized As The Founder Of American Psychology
What Is An Exponent In Mathematics
Lets discuss what Exponent is generally used interchangeably with power but it is used in a different context. While power is used to represent the whole expression, but exponent is the superscript placed above to the right of the base of any number. It is generally defined as a positive or negative number which represents the power to which the base number is raised meaning it states the number of times a number needs to be used in a multiplication process.
For example, in 53 = 5 × 5 × 5 equals to 125, the base number is equal to 5 which is used thrice in a multiplication meaning over here we are multiplying 5 three times by itself. Exponents generally go by powers or indices. Square and cube are the two most commonly used exponents in geometry.
For example, a2 is defined as a square and a3 is defined as a cube. If the exponent is equal to 1, then the result is the base number and if the exponent is 0, then the result is always equal to 1. For example, 21 is equal to 2 and 20 equals to 1.
Here are the seven laws of exponents:
What Is Exponential Form
We all must have heard the word exponential before. What does this word mean? Exponential means to become more and more rapid in growth. However, in mathematics, it represents a mathematical expression that has one or more exponents. Hence, we know it as an exponential form.
We can say that a thing may increase with an exponential rate when the increase becomes quicker and quicker as the thing which is talked about becomes larger.
Now let us learn more about the exponential form of numbers which is greatly used and applied in mathematics.
Recommended Reading: Michael Jackson Kids Biological Parents
Power Raised To A Power
According to this law, if a is the base, then the power raised to the power of base a gives the product of the powers raised to the base a, such as
- n = amn
where a is a non-zero term and m and n are integers.
Example 4: Express 83 as a power with base 2.
Solution: We have, 2×2×2 = 8 = 23
Therefore, 83= 3 = 29
Using Exponents In Calculating Population Growth
Population increase also works in this way because populations are expected to be able to produce a consistent number more offspring each generation, meaning we can develop an equation for predicting their growth over a certain amount of generations:
c = 2
In this equation, c represents the total number of children had after a certain number of generations, represented by n, which assumes that each parent couple can produce four offspring. The first generation, therefore, would have four children because two multiplied by one equals two, which would then be multiplied by the power of the exponent , equalling four. By the fourth generation, the population would be increased by 216 children.
In order to calculate this growth as a total, one would then have to plug the number of children into an equation that also adds in the parents each generation: p = 2+ c + 2. In this equation, the total population is determined by the generation and the total number of children added that generation .
The first part of this new equation simply adds the number of offspring produced by each generation before it , meaning it adds the parents’ total to the total number of offspring produced before adding in the first two parents that started the population.
Don’t Miss: Blanket Jackson Biological Dad