Solved Examples For You
Question 2: If l is any given line an P is any point not lying on l, then the number of parallel lines drawn through P, parallel to l would be:
Answer : The correct option is A. Draw a line l and a point P not lying on l. Now we can draw a straight line parallel to l, which passes through P. We can see that only one line is drawn which is parallel;to l and passes through P.
Question 2: Identify the given angle in the diagram.
Answer : The correct option is D. The angles opposite to the sides of the transversal line and which is exterior is Alternate Exterior Angles.
Question 3: What is an example of a corresponding angle?
Answer: You already know that the transversal is when a line crosses two other lines, similarly, the angles in matching corners are referred to as corresponding angles. For instance, a and e are corresponding angles. Thus, when these two lines are parallel, the corresponding angles are equal.
Question 4: What is the sum of two corresponding angles?
Answer: As it is known that corresponding angles can be supplementary when the transversal intersects two parallel lines perpendicularly this is at 90 degrees. Thus, in such a case, each of the corresponding angles is going to be 90 degrees and their sum will add up to 180 degrees which is supplementary.
Question 5: What is a transversal?
Question 6: State the properties of a transversal.
What Is The Transversal Theorem
Various theorems are defined for transversal, such as:
1. If a transversal intersects two parallel lines, then each pair of corresponding angles is equal.
2. If a transversal intersects two lines such that a pair of corresponding angles are equal, then the two lines are parallel to each other.
3. If a transversal intersects two lines such that a pair of alternate interior angles are equal, then the two lines are parallel.
4. If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.
Summary Of Parallel Lines Definition
Lets summarize what weve learned so far about parallel lines:
- they are coplanar lines
The properties below will help us determine and show that two lines are parallel.
1.; Corresponding angles are equal.
; ; ; Example: $\angle b ^ = \angle f^, \angle a ^ = \angle e^e$
2. Alternate interior angles are equal.;
; ; ; Example: $\angle c ^ = \angle f^, \angle d ^ = \angle e^$
3. Alternate exterior angles are equal.;
; ; ; Example: $\angle a ^ = \angle h^, \angle b^ = \angle g^$
4. Consecutive interior angles add up to $180^$.
; ; ; Example: $\angle c ^ + \angle e^=180^$, $\angle d ^ + \angle f^=180^$
5. Consecutive exterior angles add up to $180^$.
; ; ; Example: $\angle a^ + \angle g^=$180^$, $\angle b ^ + \angle h^=$180^$
Lets try to answer the examples shown below using the definitions and properties weve just learned.
Example 1
Which of the following term/s does not describe a pair of parallel lines?
; ; ;a. Noncoplanar
; ; ;d. Same direction
Solution
Go back to the definition of parallel lines: they are coplanar lines sharing the same distance but never meet. This shows that parallel lines are never noncoplanar.
Example 2
Which of the following real-world examples do not represent a pair of parallel lines?
; ; ;a. Hands of a clock
; ; ;b. Windscreen wipers
; ; ;d. Vertical strings of a tennis rackets net
Solution;
The options in;b,;c, and d are objects that share the same directions, but they will never meet. They all lie on the same plane .;
Hence, the correct answer is a.
Example 3
Solution
Example 4
Solution
Example 5
Don’t Miss: Solving Volume Problems Lesson 9-5 Answer Key
Parallel Lines And Transversals Postulates
Parallel lines and transversals are very important to the study of geometry because they enable us to define congruent .
How?
Well, when two parallel lines are cut by a transversal , then not only do we notice the vertical angles and linear pairs that are subsequently formed, but the following angle pair relationships are created as well:
- Corresponding Angles are congruent
- Alternate Exterior Angles are congruent
- Alternate Interior Angles are congruent
- Same Side Interior Angles sum to 180 degrees
And knowing how to identify these angle pair relationships is crucial for proving two lines are parallel, as Study.Com accurately states.
In the video below, youll discover that if two lines are parallel and are cut by a transversal, then all pairs of corresponding angles are congruent , all pairs of alternate exterior angles are congruent, all pairs of alternate interior angles are congruent, and same side interior angles are supplementary!
How Do You Find The Intersection Of Two Lines
Heres the summary of our methods:
Recommended Reading: Ccl4 Lewis Structure Molecular Geometry
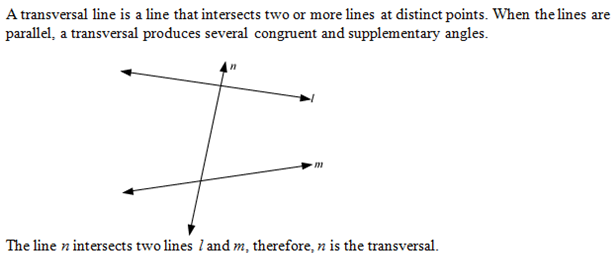
Transversals And Transversal Lines
In geometry, a transversal is any line that intersects two straight lines at distinct points. In the following figure, L is the transversal line that cuts \ and \ lines at two distinct points. In the universe of parallel and transverse lines, a transversal line connects the two parallel lines.
From the diagram, we can say that ‘L is a transversal, cutting the lines \ and \’, and thus line L is the transversal line. Here, there is no relationship between the angles formed as the lines are not parallel. Let us now see how to construct a transversal on parallel lines and what are the properties of transversal angles.
Parallel Lines Cut By A Transversal Fully Explained W/ 23 Examples
// Last Updated:
In this critical , youll learn all about parallel lines cut by a transversal.
Jenn, Founder Calcworkshop®, 15+ Years Experience
Youll gain experience classifying line types, identifying angle relationships, and finally using that knowledge to solve problems for missing angles.
Let jump in!
Read Also: Ccl4 Shape
Properties Of A Transversal Of Parallel Lines
If the transversal cuts across parallel lines there is one key property to note: The corresponding angles around each intersection are equal in measure. In the figure above, you can see that the four angles around the point E look just the same as the four angles around the point F. Drag the points A and B and convince yourself this is so.
From this central fact, other named pairs of angles are derived described on other pages. But for now, remember that there are two sets of four angles, and all angles in each set are equal in measure. In the figure above, all the red angles are equal and all the gray angles are equal no matter how you move the points A and B.
At each point E, F there are two pairs of vertical angles which are equal as shown on the right. Since the points E and F are identicalarrangements, the two corresponding pairs at E and F are equal also.
Corresponding Angles Formed By Non
For non-parallel lines, if a transversal intersects them, then the corresponding angles formed doesnt have any relation with each other. They are not equal as in the case of parallel lines but all are corresponding to each other.
Corresponding Angles;Formed by Non-Parallel Lines and Transversals
In the same, there is no relationship between the interior angles, exterior angles, vertically opposite angles and consecutive angles, in the case of the intersection of two non-parallel lines by a transversal.
Read Also: Segment Addition Postulate Color By Number Worksheet Answer Key
Can The Parallel Postulate Be Proven
Every attempt at proving the parallel postulate as a theorem was doomed to failure because the parallel postulate is independent from the other axioms and postulates. We can formulate geometry without the parallel postulate, or with a different version of the postulate, in a way that adheres to all the other axioms.
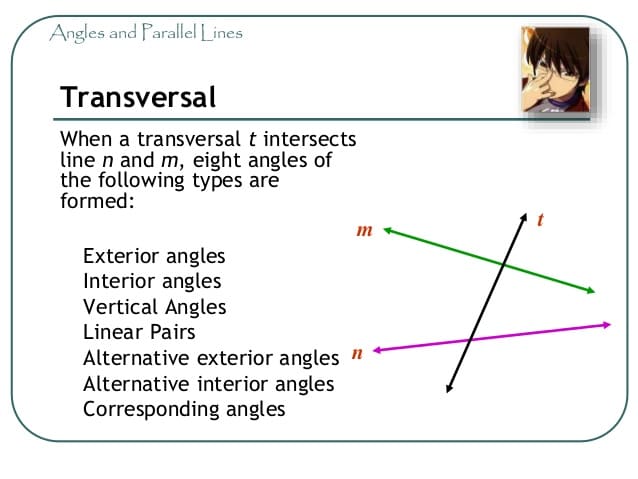
Angles Of A Transversal
A transversal produces 8 angles, as shown in the graph at the above left:
- 4 with each of the two lines, namely , , and and then 1, 1, 1 and 1; and
- 4 of which are interior , namely , , 1 and 1 and 4 of which are exterior, namely 1, 1, and .
A transversal that cuts two parallel lines at right angles is called a perpendicular transversal. In this case, all 8 angles are right angles
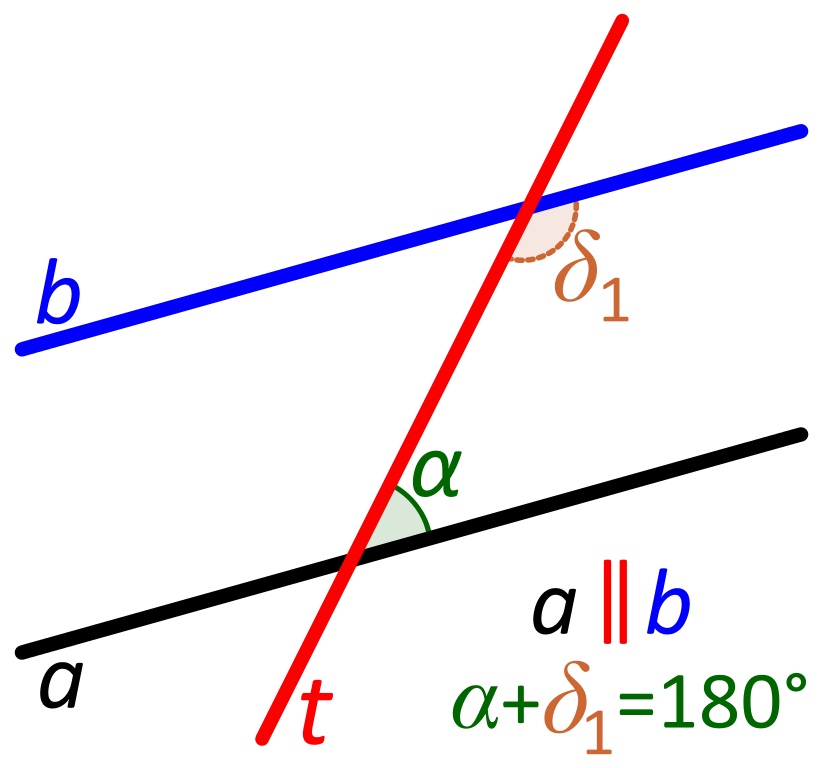
When the lines are parallel, a case that is often considered, a transversal produces several congruent and several supplementary angles. Some of these angle pairs have specific names and are discussed below:corresponding angles, alternate angles, and consecutive angles.
Alternate angles are the four pairs of angles that:
- have distinct vertex points,
- lie on opposite sides of the transversal and
- both angles are interior or both angles are exterior.
If the two angles of one pair are congruent , then the angles of each of the other pairs are also congruent.
Proposition 1.27 of Euclid’s Elements, a theorem of absolute geometry , proves that if the angles of a pair of alternate angles of a transversal are congruent then the two lines are parallel .
It follows from Euclid’s parallel postulate that if the two lines are parallel, then the angles of a pair of alternate angles of a transversal are congruent .
Corresponding angles are the four pairs of angles that:
You May Like: Exponential Growth And Decay Algebra 1 Worksheet
What Are Parallel Lines
What comes to mind when you think of parallel lines?
Is it the definition, which states that parallel lines are coplanar and never intersect because they are the same distance apart?
Or perhaps you envision two lines that have the same slope and different y-intercepts as we learned in Algebra?
Or maybe its just a visual image like a railroad track or a picket fence.
Parallel Lines Examples
What Does The Parallel Postulate Guarantee
What does the parallel postulate guarantee? Parallel postulate, One of the five postulates, or axioms, of Euclid underpinning Euclidean geometry. It states that through any given point not on a line there passes exactly one line parallel to that line in the same plane.
What is the importance of the parallel postulate in geometry?;Euclids Parallel Postulate allows that transversal to create many different angles as it cuts across the two lines, but it all boils down to only three possibilities: The lines are not parallel and two same-side interior angles are less than 180°; the lines will eventually meet on that side of the transversal.
What are the consequences of the parallel postulate?;One consequence of the Euclidean Parallel Postulate is the well- known fact that the sum of the interior angles of a triangle in Euclidean geometry is constant whatever the shape of the triangle. 2.2. 1 Theorem. In Euclidean geometry the sum of the interior angles of any triangle is always 180°.
How do you use parallel postulates?;The parallel postulate states that if a straight line intersects two straight lines forming two interior angles on the same side that add up to less than 180 degrees, then the two lines, if extended indefinitely, will meet on that side on which the angles add up to less than 180 degrees.
You May Like: Fsa Answers 2021
Definition Of Transversal In Geometry
A transversal is a line that intersects two or more other lines on a plane at two or more distinct points.
In the figure above, the red line is a transversal.
- A transversal does not have to cross parallel lines.
- A line that crosses only one line is not a transversal.
- It is not proper to say “transversal line” since the word transversal already means line.
- In practice, a transversal usually cuts parallel lines.
What is a repeating decimal ? A repeating decimal is a decimal in which …
What is a reflex angle in geometry ? Definition and examples.
Would you prefer to share this page with others by linking to it?
What is a repeating decimal ? A repeating decimal is a decimal in which …
What is a reflex angle in geometry ? Definition and examples.
What Does Transversal Mean In Geometry
In geometry, a transversal is a line, ray, or line segment that intersects other lines, rays, or line segments on a plane at different intersecting points. When it intersects parallel lines, there formed several angles that share a common property, on the other hand when a transversal intersects two or more non-parallel lines, there is no relationship between the angles formed.
Also Check: Eoc Fsa Warm Ups Algebra 1 Answers
Angles Parallel Lines And Transversals
Two lines that are stretched into infinity and still never intersect are called coplanar lines and are said to be parallel lines. The symbol for “parallel to” is //.
If we have two lines and have a third line that crosses them as in the figure below – the crossing line is called a transversal:
In the following figure:
If we draw to parallel lines and then draw a line transversal through them we will get eight different angles.
The eight angles will together form four pairs of corresponding angles. Angles F and B in the figure above constitutes one of the pairs. Corresponding angles are congruent if the two lines are parallel. All angles that have the same position with regards to the parallel lines and the transversal are corresponding pairs.
Angles that are in the area between the parallel lines like angle H and C above are called interior angles whereas the angles that are on the outside of the two parallel lines like D and G are called exterior angles.
Angles that are on the opposite sides of the transversal are called alternate angles e.g. H and B.
Angles that share the same vertex and have a common ray, like angles G and F or C and B in the figure above are called adjacent angles. As in this case where the adjacent angles are formed by two lines intersecting we will get two pairs of adjacent angles that are both supplementary.
Two angles that are opposite each other as D and B in the figure above are called vertical angles. Vertical angles are always congruent.
Parallel Lines Cut By A Transversal Lesson & Examples
1 hr 10 min
- What are parallel, intersecting, and skew lines?
- 00:09:34 Overview of transversal and angle pair relationships
- 00:20:52 Theorems for perpendicular and parallel lines
- 00:28:47 Find the measure of each angle given two parallel lines cut by a transversal
- 00:46:05
- From the given information can you prove the two lines are parallel?
- 00:55:01 Write a two-column proof given parallel lines
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
You May Like: Ccl4 Dot Structure
Parallel Lines And Transversal
Do you know what Parallel Lines are? You will understand this with the following examples. Every one;of you must have seen the pair of railway tracks or a ladder or piano keys. What is one common thing among all these? The two tracks never meet each other, also the two sides of the ladder never intersect each other. The keys of the piano are always parallel;to each other. Let us now study parallel and transversal lines and;corresponding angles in detail.
What Does P And Q Stand For In Geometry
4.1/5pqmeanspqpqpqqppq
First, P is the first letter of the word “proposition”. Old logic texts sometimes say something like “assume a proposition P” and then go on to prove something about P. Q is just the next letter after P, so when you need another proposition to assume, it’s an easy and convenient letter to use.
Secondly, what does Pvq mean? v: This means “or.” The sentence is true if and only if p is true, or q is true, or is true. ->: This means “implies.” The sentence is true if and only if the p is false or q is true vq) is true).
Consequently, what does P stand for in geometry?
Height of Prism.
Is p q True or false?
If p and q are propositions, the conjunction of p and q, pq, is true when both p and q are true, and is false otherwise. If p and q are propositions, the disjunction of p and q, pq, is false when both p and q are false, and is true otherwise.
Read Also: Algebra 1 Eoc Answers 2015
Constructing A Transversal On Parallel Lines
The construction of a transversal is easy. First, we create two parallel lines. We construct the angle on the first line as shown.
Further, we extend this constructed angle up to a point it covers both the parallel lines as done here. Here is what we get: A transversal on the two parallel lines at the desired angle .
Who Killed Naz In Intersection
All the evidence that emerged after the death of Naz shows Ali Nejat as a killer. Knowing that the Karasu family should destroy Ali Najat first in order to bring it to the end, Murat binds Ali Najats arm with his traps. While there is no one to save Ali Nejat, Kaan steals someones door without telling anyone.
Also Check: Copulation Definition Biology
Corresponding Angles Examples And Types
Examples of the corresponding angle are any angles which are formed on the opposite side of the transversal. Now, it should be noted that the transversal can intersect either two parallel line or two non-parallel lines. Thus, corresponding angles can be of two types:
- Corresponding angles formed by parallel lines and transversals
- Corresponding angles formed by non-parallel lines and transversals
In Maths, you must have learned about different types of lines and angles. Here we will discuss only corresponding angles formed by the intersection of two lines by a transversal. The two lines could be parallel or non-parallel. So, let us learn corresponding angles for both the cases.