Or * Or Multiplication
These symbols have the same meaning commonly × is used to mean multiplication when handwritten or used on a calculator 2 × 2, for example.
The symbol * is used in spreadsheets and other computer applications to indicate a multiplication, although * does have other more complex meanings in mathematics.
Less commonly, multiplication may also be symbolised by a dot . or indeed by no symbol at all. For example, if you see a number written outside brackets with no operator , then it should be multiplied by the contents of the brackets: 2 is the same as 2×.
See our page on Multiplication for more.
Factoring Numbers And Basic Algebraic Expressions
Factoring Other Forms Of Equations
Recommended Reading: What Are The Different Kinds Of Reasoning In Geometry
How To Factor Expressions With Examples
- Turito Team USA
Doesnt it get complicated when you try to solve a lengthy equation or expression and end up doomed while doing calculations? Thats when factoring expressions come in handy.
Factor expressions, also known as factoring, mean rewriting the expression as the product of factors. For example, 3x + 12y can be factored into a simple expression of 3 . In this way, the calculations become easier. The terms 3 and are known as factors. Hence, an equation can have an end number of factors, depending on the length of the expression.
Factoring expressions is one of the most used mathematical operations while performing any calculation. Even if you wish to ease or quickly perform the regular, day-to-day calculations, you can use factoring expressions. For instance, multiplying 300 with 15 might sound tricky. The calculation gets swift if you do the multiplication of factors, such as multiplying 300 with 10 and 300 with 5 and then adding the terms. Hence, how do you factor an expression judges your problem-solving ability.
Why Is Factoring So Important In Algebra
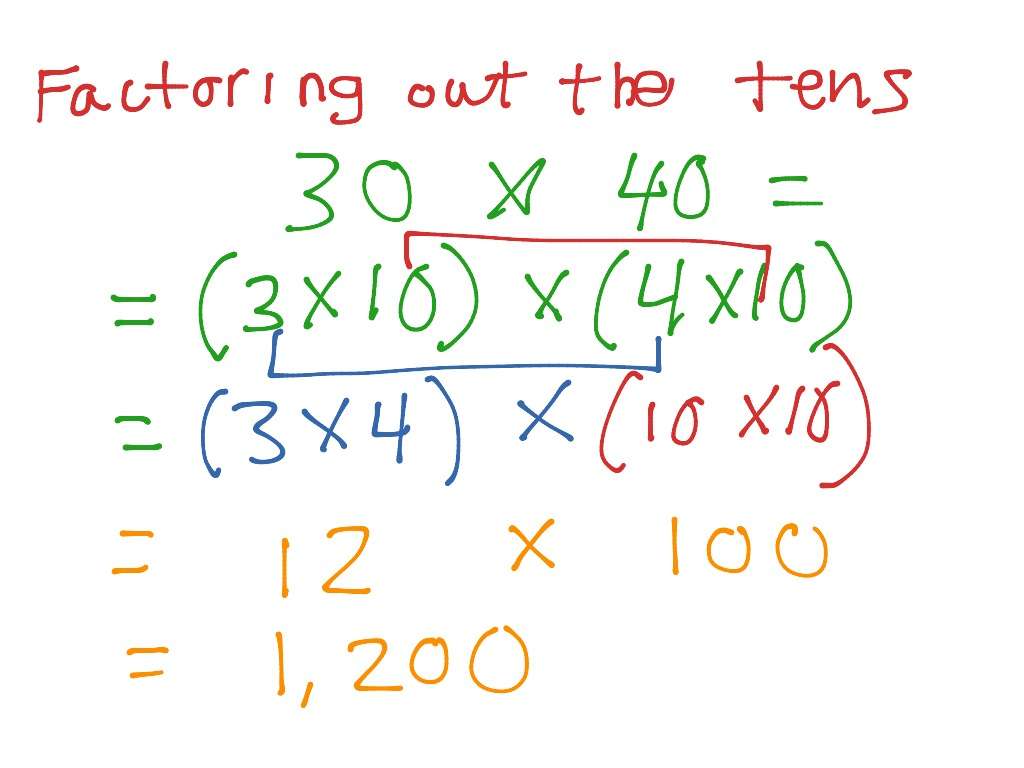
Besides, what is Factorising in math?
Factorising is the reverse of expanding brackets, so it is, for example, putting 2x² + x 3 into the form . This is an important way of solving quadratic equations. The first step of factorising an expression is to take out any common factors which the terms have.
What is the method of factoring?
Factoring Polynomials. A common method of factoring numbers is to completely factor the number into positive prime factors. A prime number is a number whose only positive factors are 1 and itself. For example 2, 3, 5, and 7 are all examples of prime numbers.
What is the factorization in math?
In mathematics, factorization or factoring consists of writing a number or another mathematical object as a product of several factors, usually smaller or simpler objects of the same kind.
Read Also: What Is Earthquake In Geography
How To Find Factors Of A Number
Knowing how to calculate factors of a number is extremely crucial in Maths. The steps to find the factors of a number are given below in a very easy to understand way. An example is taken to make the explanation easier.
Find the factors of 16.
Step 1: Write the numbers from 1 to 16
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16
Step 2: Check now, which number can divide the 16 equally from the above list of numbers.
16/1 = 16
In the same way, divide 16 by each of these numbers.
Step 3: Hence, we get the factors of 16 are 1,2,4,8, and 16
+ Addition Plus Positive
The addition symbol + is usually used to indicate that two or more numbers should be added together, for example, 2 + 2.
The + symbol can also be used to indicate a positive number although this is less common, for example, +2. Our page on Positive and Negative Numbers explains that a number without a sign is considered to be positive, so the plus is not usually necessary.
See our page on Addition for more.
Read Also: What Does Q Mean In Physics
Examples Of Factor In A Sentence
factorsfactorfactorsfactor BostonGlobe.comfactor Wiredfactor Varietyfactor The Enquirerfactor alfactor Washington PostfactorAnchorage Daily Newsfactor CNNfactor BostonGlobe.comfactor CNNfactor Forbesfactor BGRfactor Washington Postfactor alfactor New York Timesfactor SFChronicle.com
These example sentences are selected automatically from various online news sources to reflect current usage of the word ‘factor.’ Views expressed in the examples do not represent the opinion of Merriam-Webster or its editors. Send us feedback.
Factors Of Square Numbers
Square numbers are those that produced when a number is multiplied by itself. It is represented as nx n = n2, where n is any integer.
2 x 2 = 22 = 4
3 x 3 = 32 = 9
5 x 5 = 52 = 25
10 x 10 = 102 = 100
The above examples prove that one of the factors of a square number is the value, that is square to produce the original number.
Also Check: What Are Human And Physical Features In Geography
Multiples And Factors In Ks1 And Ks2
In Year 2, children are expected to recognise multiples of:
- 2
- 5
- and 10 .
The foundation for this knowledge is started in Year 1 where children practise counting in 2s, 5s and 10s.
In Year 3, children need to be able to recognise multiples of 2, 5 and 10 up to 1000.
They would be taught the rule that any number that has a last digit that is even is a multiple of 2. They would also learn that any number ending in a 5 or 0 is a multiple of 5. And finally, any number that ends in a 0 is a multiple of 10.
By Year 4, when children have learnt all their times tables they should be able to recognise multiples of any number up to 10.
For example, they may be given a number such as 24 and asked if it is a multiple of the following numbers: 10, 2, 5, 8, 6. Their knowledge of times tables should help them to work out that 24 is a multiple of 2, 8 and 6.
Children also learn about factors in Year 4.
They may be asked to identify pairs of factors of two-digit numbers.
- For example: they may be given the number 60 and asked to pick out two pairs of factors from the following numbers: 7, 3, 9, 8, 15, 4, 20.
- They may also need to find common multiples. For example: they may be given the numbers 6 and 9 and asked to find three multiples that have both these numbers as factors.
In Year 5, children will continue to carry out tasks involving factors and multiples and this will extend to learning about prime numbers and square numbers.
Webster Dictionaryrate This Definition:
Factornoun
one who transacts business for another an agent a substitute especially, a mercantile agent who buys and sells goods and transacts business for others in commission a commission merchant or consignee. He may be a home factor or a foreign factor. He may buy and sell in his own name, and he is intrusted with the possession and control of the goods and in these respects he differs from a broker
Factornoun
a steward or bailiff of an estate
Factornoun
one of the elements or quantities which, when multiplied together, from a product
Factornoun
one of the elements, circumstances, or influences which contribute to produce a result a constituent
Factorverb
to resolve into its factors
Etymology:
You May Like: What Are Grid Lines In Geography
Factoring The Gcf From An Expression
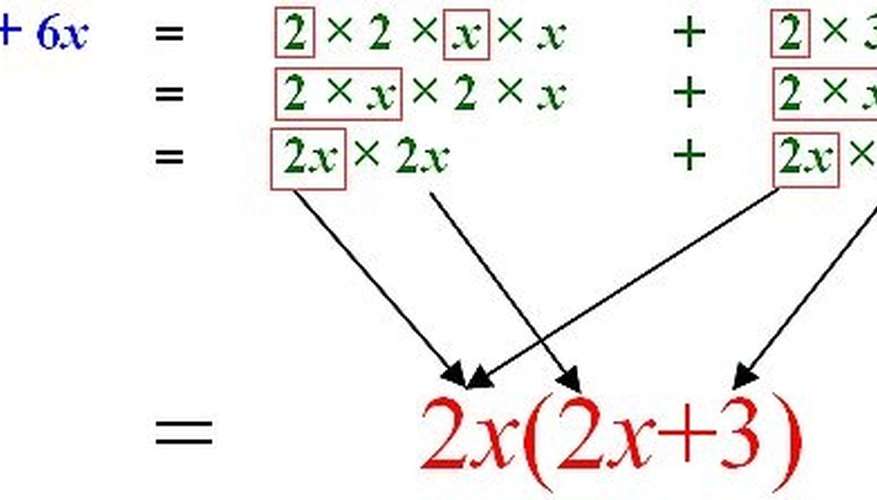
And no, I don’t mean factoring the expression of your boss as you tell him you accidentally flooded the break room with coffee.Algebraic expressions consist of numbers, which are called coefficients, and variables, which can be raised to a power. In the expression x^2 + 6x + 8, 1 is the coefficient of x^2, the variable. Likewise, 6 is a coefficient of x^1. 8 is called a constant – it is not multiplied by a variable. .To factor an expression, you have to start by factoring out the GCF, or Greatest Common Factor. List the factors of each component of the expression. Here we are interested in finding the natural number factors.The expression x^2 + 6x + 8 would have factors that look like this:x^2: 1
History Of Factorization Of Expressions

The systematic use of algebraic manipulations for simplifying expressions ) may be dated to 9th century, with al-Khwarizmi‘s book The Compendious Book on Calculation by Completion and Balancing, which is titled with two such types of manipulation.
However, even for solving quadratic equations, the factoring method was not used before Harriot‘s work published in 1631, ten years after his death. In his book Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas, Harriot drew, tables for addition, subtraction, multiplication and division of monomials, binomials, and trinomials. Then, in a second section, he set up the equation aa ba + ca = + bc, and showed that this matches the form of multiplication he had previously provided, giving the factorization .
You May Like: What Is Stimulation In Biology
How To Find Factors Of Large Numbers
To calculate the factors of large numbers, divide the numbers with the least prime number, i.e. 2. If the number is not divisible by 2, move to the next prime numbers, i.e. 3 and so on until 1 is reached. Below is an example to find the factors of a large number.
Example: 1420
| 5 | 71 |
In step 3, a prime number is obtained as a product, and so, the process is stopped. The factors will be all the multiples of 1, 2, 2, 5, 71, 355, 710. Now, the positive factors of 1420 will be 1, 2, 4, 5, 10, 20, 71, 142, 284, 355, 710, and 1420.
In the same case, if only prime factors are considered, it is called the prime factorization of that number. In this way, it is easy to factor a number and know its factors and prime factors.
What Are The Factors
When a number is said to be a factor of any other second number, then the first number must divide the second number completely without leaving any remainder. In simple words, if a number is exactly divisible by any number , then the divisor is a factor of that dividend. Every number has a common factor that is one and the number itself.
For example, 4 is a factor of 24, i.e. 4 divides 24 exactly giving 6 as quotient and leaving zero as remainder. Alternatively, 6 is also a factor of 24 as it gives 4 as quotient on division. Therefore, 24 has 1, 24, 4, 6 as its factors in addition to 2, 3, 8 and 12 and all these numbers divide 24 exactly leaving no remainder.
If any natural number has only two factors, i.e. 1 and the number itself as its factors, such numbers are called prime numbers. 2 is an example of a prime number where it has only two factors, i.e. 1 and 2.
Recommended Reading: How Do You Find Volume In Chemistry
How Do You Factor A Quadratic Equation
Factoring Polynomials By Grouping
Sometimes you will get four or more terms, that look something like this:2x^2 + 6x^3 + 5x^7 + 15x^8There is no common coefficient, and factoring out x^2 doesn’t help much. This is where you would use grouping to factor.Grouping means factoring out the GCF of only two terms of the expression. You can see that 2x^2 + 6x^3 and 5x^7 + 15x^8 both can have a GCF taken out. Do so.2x^2 + 5x^7 Note that there is a common factor, 1+3x. This expression can be rephrased to . There’s your answer.Note that can be factored further by factoring out an x^2 from the first binomial: x^2 .
Don’t Miss: How Did Geography Impact The Development Of Agricultural Societies
Example: Factor 4×2 9
Hmmm… there don’t seem to be any common factors.
But knowing the Special Binomial Products gives us a clue called the “difference of squares”:
Because 4×2 is 2, and 9 is 2,
So we have:
And that can be produced by the difference of squares formula:
= a2 b2
Where a is 2x, and b is 3.
So let us try doing that:
= 2 2 = 4×2 9
Yes!
So the factors of 4×2 9 are and :
Answer: 4×2 9 =
How can you learn to do that? By getting lots of practice, and knowing “Identities”!
Here is a list of common “Identities” .
It is worth remembering these, as they can make factoring easier.
| a2 b2 |
There are many more like those, but those are the most useful ones.
Common Mathematical Symbols And Terminology: Maths Glossary
Mathematical symbols and terminology can be confusing and can be a barrier to learning and understanding basic numeracy.
This page complements our numeracy skills pages and provides a quick glossary of common mathematical symbols and terminology with concise definitions.
Are we missing something? Get it touch to let us know.
Recommended Reading: How Do You Do Average In Math
Shortcut Method To Find Factors Of A Number
Let us see an example, to find the factors of a number using the shortcut method.
Consider the number as 40.
40 = 10 × 4
Now, the factors of 40 will include all the combinations from 5 × 2 × 2 × 2 and 1 itself . So, the positive factors of 40 are 1, 2, 4, 5, 8, 10, 20, and 40. It should be noted that there will also be negative factors whose count has to be even.
What Is The Smallest Factor Of 9
The factors of 9 are 1, 3 and 9. Then the smallest factor of 9 is 1.
To solve problems on the topic, download BYJUS-The Learning App from Google Play Store and watch interactive videos. Also, take free tests to practice for exams. To study about other topics, visit http://www.byjus.com/ and browse among thousands of interesting articles.
Put your understanding of this concept to test by answering a few MCQs. Click Start Quiz to begin!
Select the correct answer and click on the Finish buttonCheck your score and answers at the end of the quiz
Recommended Reading: What Is Red Shift In Physics
Finding Factors Using Multiplication Method
In order to find the factors of a number using the multiplication method, we need to use a similar procedure as given above except for a few changes. Let us learn this method with the help of an example.
Example: Find the factors of 24 using the multiplication method.
Solution: Let us find the factors of 24 by multiplication method using the following steps.
- Step 1: In order to find the factors of 24 using multiplication, we need to check what pairs of numbers multiply to give us 24, so we need to divide 24 by natural numbers starting from 1 and go on till 9.
- Step 2: We write that particular number along with its pair and make a list as shown in the figure given above. As we check and list all the numbers up to 9, we automatically get the other pair factor along with it. For example, starting from 1, we write 1 × 24 = 24 and 2 × 12 = 24 and so on. Here, forms the first pair, forms the second pair and the list goes on as shown. So, as we write 1 as the factor of 24, we get the other factor as 24 and as we write 2 as the factor of 24, we get 12 as the other factor. In this way, we get all the factors.
- Step 3: After the list is noted, we get all the factors of 24 starting from 1 up there, coming down and then we go up again up to 24. This gives us a complete list of all the factors of 24 as shown in the figure given above.
Therefore, the factors of 24 can be listed as 1, 2, 3, 4, 6, 8, 12, and 24.