Ring Of Light Around The Source
Look at any source of light around you right now, you may observe the light does not directly get transmitted in the forward direction, a small part of the light energy is diffracted around the source. This diffraction of light occurs due to the presence of dust and gaseous particles present nearby.
Small Versus Large Sensors
It is often said that crop-sensor cameras show diffraction more easily than full-frame cameras . Is this a myth, or does it hold true?
Lets start with what we know. At a given aperture on a lens, the Airy disk will always be the same physical size. It doesnt matter what sensor you use this is a property of physics that only depends upon the aperture itself. For example, whether I put a 50mm f/1.8 lens on the full-frame D750 or the crop-sensor D3300, the size of its Airy disk projection will be identical .
So, wheres the confusion? The issue irises from the fact that the same Airy disk takes up a larger percentage of a crop-sensor camera than a full-frame camera. Take a look at the example below:
In fact, at an equal print size, a DX camera will show more diffraction than an FX camera. This is because the DX sensor is essentially a crop of the FX sensor in other words, it magnifies everything in your photograph including the diffraction just like cropping in post-production.
The amount of additional diffraction is the same as your crop factor. So, for a 1.5x crop-sensor camera, multiply your aperture by 1.5 in order to see the equivalent diffraction on a full-frame camera. For example, the Airy disk at f/11 on a DX camera takes up roughly the same percentage of your sensor as the Airy disk at f/16 would on a full-frame camera.
Sound Waves And Water Waves
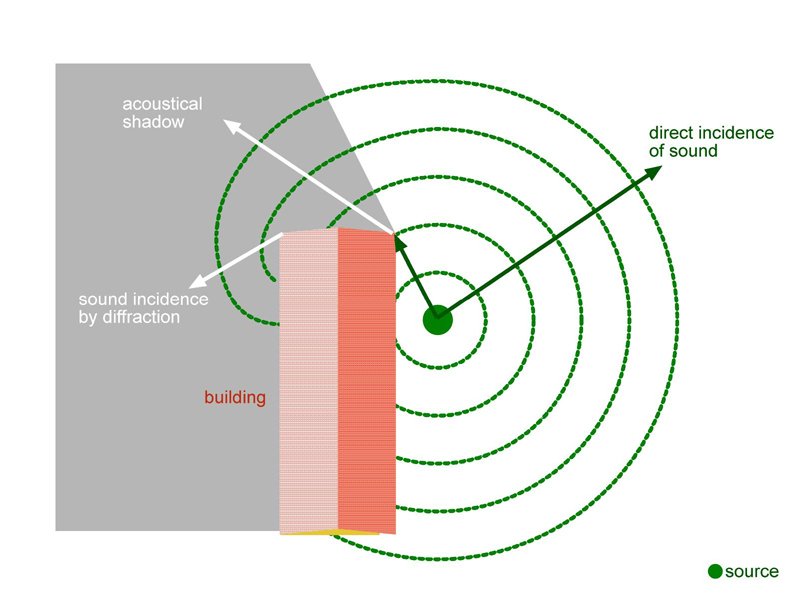
While placing obstacles between a person and a source of sound can reduce the intensity of sound the person hears, the person can still hear it. This is because sound is a wave, and therefore diffracts, or bends, around corners and obstacles.
If Fred is in one room, and Dianne in another, when Dianne shouts something to Fred he will hear it as if she were shouting from the doorway, regardless of where she is in the other room. That’s because the doorway acts as a secondary source of the sound waves. Likewise, if a member of the audience at an orchestra performance sits behind a pillar, they can still hear the orchestra just fine the sound has a long enough wavelength to bend around the pillar .
Ocean waves also diffract around features like jetties, or the corners of coves. Small surface waves will also bend around obstacles like boats, and turn into circular wave fronts when passing through a small opening.
You May Like: Evaluating Functions Worksheet Algebra 2 Answer Key
Examples And Applications Of Diffraction
Image Courtesy: Satyam Bhuyan
Circular Aperture Diffraction Equations
Our discussions of diffraction have used a slit as the aperture through which light is diffracted. However, all optical instruments have circular apertures, for example the pupil of an eye or the circular diaphragm and lenses of a microscope. Circular apertures produce diffraction patterns similar to those described above, except the pattern naturally exhibits a circular symmetry. Mathematical analysis of the diffraction patterns produced by a circular aperture is described by the diffraction equation:
sin = 1.22
where is the angular position of the first order diffraction minima , is the wavelength of the incident light, d is the diameter of the aperture, and 1.22 is a constant. Under most circumstances, the angle is very small so the approximation that the sin and tan of the angle are almost equal yields:
1.22
Thus, if two objects reside a distance D apart from each other and are at a distance L from an observer, the angle between them is:
= D / L
which leads us to be able to condense the last two equations to yield:
D = 1.22
Where D is the minimum separation distance between the objects that will allow them to be resolved. Using this diffraction equation, the human eye can resolve objects separated by a distance of 0.056 millimeters, however the photoreceptors in the retina are not quite close enough together to permit this degree of resolution, and 0.1 millimeters is a more realistic number under normal circumstances.
Contributing Authors
Don’t Miss: What Is An Example Of Movement In Geography
Introduction To Diffraction Of Waves
What happens to water when you put a finger under the tap? Does water turn back on the tap or it continues falling down? Is the direction of water the same as before putting the finger under the tap? Why?
What happens to water waves when they encounter a stone during their path? Do they turn back or they continue moving on their way?
What occurs to the shape of waves when they pass through a narrow gap? Do waves have the same shape as before?
All these questions will get answer in this tutorial. Therefore, please read it before jumping to other tutorials as this tutorial sheds light to many questions which will arise during the study of waves. Also, the information provided in this tutorial will form the base for the next section.
Diffraction And Depth Of Field
Diffraction decreases a photographs sharpness at small apertures. Yet, at the same time, small apertures increase the amount of depth of field in a photograph. This is not a contradiction, although it can be confusing at first. Look, for example, at the comparison below:
As you can tell, the f/22 photo has much more of the scene within its depth of field. If I want this entire subject to be sharp, it is far better than the photograph at f/5.6. However, lets look at the point of focus more closely:
As you can see, the f/5.6 photo is significantly sharper.
This, of course, does not mean that you should shoot every photograph at f/5.6. If you need a large depth of field, feel free to use smaller apertures sometimes, its worth the slight reduction in sharpness from diffraction.
Don’t Miss: How To Intimidate Someone Psychologically
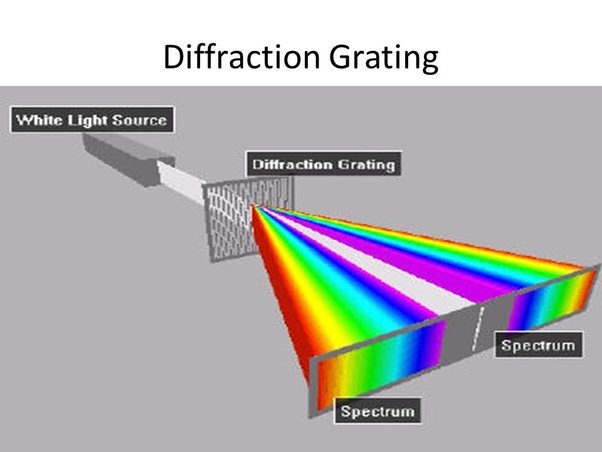
Double Slit And Diffraction Gratings
A slightly different diffraction pattern can also be obtained by passing light through two small slits separated by distance in a double-slit experiment. Here we see constructive interference on the wall anytime the path-length difference between light coming from the two slits is a multiple of the wavelength .
The path difference between parallel waves from each slit is dsin, where d is the distance between the slits. To arrive in-phase, and constructively interfere, this path difference must be a multiple of the wavelength . The equation for the locations of the intensity maximas is therefore n = dsin , where n is any integer.
Note the differences between this equation and the corresponding one for single-slit diffraction: This equation is for maxima, rather than minima, and it uses the distance between the slits rather than the width of the slit. In addition, n can equal zero in this equation, which corresponds to the main maximum in the center of the diffraction pattern.
This experiment is often used to determine the wavelength of the incident light. If the distance between the central maximum and the adjacent maximum in the diffraction pattern is x, and the distance between the slit surface and the wall is L, the small angle approximation can be used:
Substituting this in the previous equation, with n=1, gives:
Propagation Of A Laser Beam
The way in which the beam profile of a laser beam changes as it propagates is determined by diffraction. When the entire emitted beam has a planar, spatially coherent wave front, it approximates Gaussian beam profile and has the lowest divergence for a given diameter. The smaller the output beam, the quicker it diverges. It is possible to reduce the divergence of a laser beam by first expanding it with one convex lens, and then collimating it with a second convex lens whose focal point is coincident with that of the first lens. The resulting beam has a larger diameter, and hence a lower divergence. Divergence of a laser beam may be reduced below the diffraction of a Gaussian beam or even reversed to convergence if the refractive index of the propagation media increases with the light intensity. This may result in a self-focusing effect.
When the wave front of the emitted beam has perturbations, only the transverse coherence length should be considered as a Gaussian beam diameter when determining the divergence of the laser beam. If the transverse coherence length in the vertical direction is higher than in horizontal, the laser beam divergence will be lower in the vertical direction than in the horizontal.
- , },\,}
where D is the diameter of the entrance pupil of the imaging lens .
Don’t Miss: Segment Addition Postulate Find The Length Indicated
What Is Fringe Width
Fringe width is defined as the distance between any two consecutive bright or dark fringes.
Stay tuned with BYJUS to know more about diffraction of light, refraction, reflection, interference and other related concepts with the help of interactive video lessons.
Put your understanding of this concept to test by answering a few MCQs. Click Start Quiz to begin!
Select the correct answer and click on the Finish buttonCheck your score and answers at the end of the quiz
Diffraction In The Real World
CDs represent an example of a diffraction grating that is not made from apertures. The information on CDs is stored by a series of tiny, reflective pits in the CD surface. The diffraction pattern can be seen by using a CD to reflect light onto a white wall.
X-ray diffraction, or x-ray crystallography, is an imaging process. Crystals have a very regular, periodic structure that has units about the same length as the wavelength of x-rays. In x-ray crystallography, x-rays are emitted at a crystallized sample, and the resultant diffraction pattern is studied. The regular structure of the crystal allows the diffraction pattern to be interpreted, giving insights about the crystal’s geometry.
X-ray crystallography has been used to great success determining the molecular structures of biological compounds. The biological compounds are put into a supersaturated solution, which is then crystallized into a structure that contains a great number of molecules of the compound set in a symmetric, regular pattern. Most famously, x-ray crystallography was used by Rosalind Franklin in the 1950s to discover the double-helix structure of DNA.
Related Articles
Also Check: Why Is Ap Bio So Hard
Diffraction Of Light Definition
The diffraction of light is similar to the concept of using a loudspeaker. In a loudspeaker, you speak through a small hole, but the voice coming out spreads around the vicinity and that too modulated, i.e., the diffraction of sound.
Lets suppose that you are stuck in a tunnel and there is no one around to help you come out of it, so you try to call people moving around the tunnel but they cant hear you.
Now, you switch on the flashlight of your mobile phone, and the flashlight emitting at the opened end of the tunnel spreads around. As the light is spreading all around the area, this spreading is the diffraction of light.
If in an electric circuit, electrons passing through a narrow wire approaches a big container , these electrons spread all around, and this scattering is the electron diffraction.
Consider the below diagram to understand the cases mentioned above:
What Is The Difference Between Diffraction And Scattering
The terms diffraction and scattering are often used interchangeably and are considered to be almost synonymous. Diffraction describes a specialized case of light scattering in which an object with regularly repeating features produces an orderly diffraction of light in a diffraction pattern. In the real world, most objects are very complex in shape and should be considered to be composed of many individual diffraction features that can collectively produce a random scattering of light.
Recommended Reading: Holt Geometry Chapter 7 Test Answer Key
Is A Shadow Diffraction
Diffraction is not what makes a trees shadow blurry. The shadows of trees, buildings, and other outdoor objects are made blurry by the fact that the sun is an extended light source. Although diffraction can make shadows blurry, for human-sized objects at visible wavelengths of light, the diffraction of light is small.
What Is Diffraction Of Light
The bending of light waves around the corners of an obstacle and spreading of light waves into geometrical shadow is called diffraction. Fraunhofer Diffraction and Fresnel Diffraction are two Types of Diffraction of Light. Bending of Light around the corners of Window is an example of Diffraction.
Diffraction effect depends upon the size of the obstacle. Diffraction of light takes place if the size of the obstacle is comparable to the wavelength of light. Light waves are very small in wavelength,i.e, from 4×10-7 m to 7 × 10 -7 m. If the size of opening or obstacle is near to this limit, only then we can observe the phenomenon of diffraction.
Also Check: Holt Mcdougal Geometry Practice Workbook
What Is The Best Example Of Diffraction
The effects of diffraction are often seen in everyday life. The most striking examples of diffraction are those that involve light for example, the closely spaced tracks on a CD or DVD act as a diffraction grating to form the familiar rainbow pattern seen when looking at a disc.
Interference Patterns Of Electromagnetic Waves
Just like with other waves, light waves can interfere with each other and can diffract, or bend, around a barrier or opening. A wave diffracts more when the width of the slit or opening is closer in size to the wavelength of the light. This diffraction causes an interference pattern regions where the waves add together and regions where the waves cancel each other out. Interference patterns change with the wavelength of light, the size of the opening and the number of openings.
When a light wave encounters an opening, each wave front emerges on the other side of the opening as a circular wave front. If a wall is placed opposite to the opening, the diffraction pattern will be seen on the other side.
The diffraction pattern is a pattern of constructive and destructive interference. Because the light has to travel different distances to get to different points on the opposite wall, there will be phase differences, leading to spots of bright light and spots of no light.
Don’t Miss: Geometry Angle Addition Worksheet
What Is Single Slit Diffraction
In the single-slit diffraction experiment, we can observe the bending phenomenon of light or diffraction that causes light from a coherent source to interfere with itself and produce a distinctive pattern on the screen called the diffraction pattern. Diffraction is evident when the sources are small enough that they are relatively the size of the wavelength of light. You can see this effect in the diagram below. For large slits, the spreading out is small and generally unnoticeable.
Diffraction Facts For Kids
Diffraction is a physics concept which occurs when waves bend around small obstacles, or spread out after they pass through small openings. Diffraction occurs with all waves, including sound waves, water waves, and electromagnetic waves such as light that the eye can see. Diffraction also occurs with matter such as electrons.
You May Like: Geometry Segment Addition Postulate Worksheet
Single Slit Diffraction Formula
We shall assume the slit width a < < D. x`D is the separation between slit and source.
We shall identify the angular position of any point on the screen by measured from the slit centre which divides the slit by \ lengths. To describe the pattern, we shall first see the condition for dark fringes. Also, let us divide the slit into zones of equal widths \. Let us consider a pair of rays that emanate from distances \ from each other as shown below.
The path difference exhibited by the top two rays shown is:
| \ |
Remember that this is a calculation valid only if D is very large. For more details about the approximation check out our article on theYoungs Double Slit experiment.
We can consider any number of ray pairings that start from a distance \ from one another such as the bottom two rays in the diagram. Any arbitrary pair of rays at a distance \can be considered. We shall see the importance of this trick in a moment.
For a dark fringe, the path difference must cause destructive interference the path difference must be out of phase by \.
For the first fringe,
| L = \ = \ = a sin |
For a ray emanating from any point in the slit, there exists another ray at a distance \ that can cause destructive interference.
Thus, at = sin1a, there is destructive interference as any ray emanating from a point has a counterpart that causes destructive interference. Hence, a dark fringe is obtained.
| \ \ |
| n = a sin |