Naming Conventions For Polygons
The endpoints of each side of a polygon are the vertices of the polygon. The vertices are also referred to as corners of the polygon.
Points A, B, C, and D are vertices for the rectangle above. Polygons can be named by their vertices as long as they are listed in consecutive order. The rectangle above can be named as ABCD, CBAD, or other sequences, but not ACDB.
The vertices of a polygon are also the vertices of the interior angles of the polygon. The pentagon ABCDE below is one example.
How Do You Identify Adjacent Angles
Being able to identify a common side and a common vertex is the simplest way to identify an adjacent angle. If two angles share one side and both derive from the same corner point, then they are adjacent angles.
Its important to remember that adjacent angles must have BOTH a common side and common vertex. Therefore, if you see two angles that are coming from the same corner but there is another angle in the middle, it means that they do not share any sides. This means that they are not adjacent angles as they dont share a side AND a vertex.
Identifying adjacent angles becomes easier with practice and seeing examples will help you understand what you are looking for.
Adjacent Angles Sample Questions
Here are a few sample questions going over adjacent angles.
Question #1:
Which angles are not adjacent?
Answer:
C is the correct answer because a and b because although they share a common side, they have two different vertices. Therefore, they are not adjacent. Choices A, B, and D are incorrect because they all show angle pairs with common sides and a common vertex.
Question #4:
Juan is studying leaf veins and notices adjacent angles in the plant structure. He draws the diagram below and records four pairs of adjacent angles. One of Juans adjacent angle pairs is incorrect. Based on the diagram, which pair of angles is not adjacent?
GDI and WDI
Answer:
D is the correct answer because DEO and WDI are not adjacent angles. They do not share a side or a vertex. Choices A, B, and C are incorrect because these answer options list angle pairs with common sides and a common vertex.
Question #5:
Keisha and James are looking at a map of city streets and notice a lot of adjacent angles. James draws the image shown to illustrate the angles they find. Keisha points out that AOE and COD are adjacent because they share a vertex and one side. James disagrees. He says that these angles do not have a common side. Who is correct, and why?
James is correct because both angles share the same vertex but they do not have a common side.
Keisha is correct because both angles share the vertex O and line AD.
James is incorrect because AOE and COD do not have the same vertex.
Answer:
Read Also: Kuta Software Infinite Geometry Naming Angles Answers
Vertices Of Line Segments And Angles
When two line segments intersect, the point of the meeting of the two lines is a vertex. This is true, regardless of whether the lines cross or meet at the corner. Therefore, the angles also have vertices.
Angle measures the relationship of the two-line segments. Furthermore, these are called as rays and they meet at a specific point. So, on the basis of the above definition, one can notice that this point is also a vertex.
What Are The Properties Of Adjacent Angles
In order to further help you visualize what adjacent angles look like, heres a quick list of their properties:
Read Also: How Does Physics Relate To Chemistry
How To Measure An Acute Angle
Let us try to measure the given AOB.
- Step 1: Align the protractor with the ray OB as shown below. Start reading the inner scale from the 0° of the protractor.
- Step 2: The number on the protractor that coincides with the second ray is the measure of the angle. Measure the angle using the inner scale of the protractor. Thus, AOB = 37°
How To Construct Angles
We use a protractor to construct angles. Let us draw an angle of 50°.
- Step 1: First, draw a ray OB and align the protractor with OB as shown.
- Step 2: Using the inner scale of the protractor, mark a point A above the marking on the protractor that corresponds to 50°.
- Step 3: Remove the protractor and draw a ray beginning at O that passes through this point A. Thus, AOB is the required angle, that is, AOB = 50°.
Note: If the ray extends in the other direction, we measure the angle using the outer scale from the 0° mark on the bottom-left.
The figure given below shows how to draw an angle of 50° when the ray is pointing in the other direction.
After placing the protractor on OB, we use the outer scale and mark 50° as shown. Then, we mark that point as A and join it to point O. This forms angle AOB = 50°
Important Notes on Angles
Don’t Miss: What Is Scaffolding In Psychology
Properties Of A Vertex
- A figure or object that does not have any sides or edges does not have any vertex. For example, sphere, cylinder, and circle do not have any vertices.
- When two lines meet at a point to form a vertex, they also form an interior angle of the figure.
Examples
Q. Find the number of vertices in the given figure.
Q. Find the number of vertices in the given figure.
Q. Find the number of vertices in the given figure.
Geometry is a crucial part of mathematics that forms a large part of the curriculum for students. Advanced learning of geometry is possible only with the correct understanding of the basics of geometry. Vertex is one of the preliminary topics that make the foundation of Geometry. Help your kids learn about vertex with detailed course material from SplashLearn. The engaging games and interactive worksheets from SplashLearn provide enough practice for young learners to master the concept. So, make the most of online learning with impactful resources from SplashLearn!
How To Construct An Angle
Splashlearns vision is to transform education for K-5th grade students. It provides personalized learning for every student according to the 21st century. SplashLearn allows students to study math through a highly engaging and customized program. SplashLearn is available across all digital platforms, and more than 40 million students have used it worldwide.
To know more about angles, click here.
Don’t Miss: Does Poverty Cause Psychological Disorder
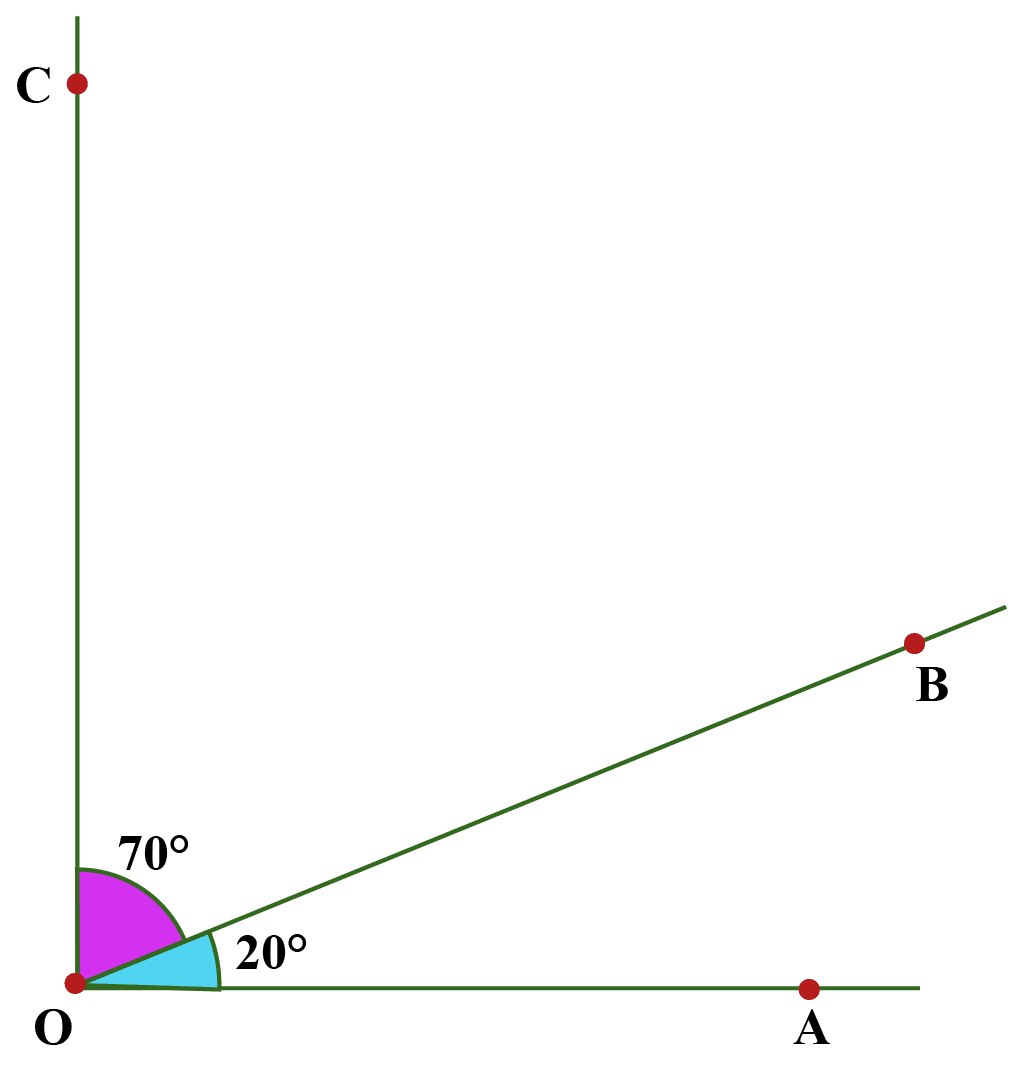
Sum Of Angles Around A Point
The sum of all the angles around a point is always 360 degrees.
For example, Sum of angles around point O is 360 degrees.
If you liked this article, here are a few more articles that you may like:
Step 3: Approach and Working out
To find Y-X, we need to find Y and X first.
Measure of angle Y:
- We are given AFC = 100° and,
- AFC + BFC = 180° as the sum of angles on the same side straight line is 180°
- 100° + BFC = 180°
Measure of angle X:
- We are given BFE = 45° and,
- DFE + BFE + BFC = 180° as the sum of angles on the same side straight line is 180°.
- X + 45° +80°= 180°
Hence, Y X = 80° 55° =25°.
Thus, the correct answer is option B.
If you are planning to take the GMAT, we can give you access to quality online content to prepare. We are the most reviewed GMAT prep company on gmatclub with more than 2200+ reviews, as of 4th October 2021.
Vertices In Computer Graphics
In computer graphics, objects are often represented as triangulated polyhedra in which the object vertices are associated not only with three spatial coordinates but also with other graphical information necessary to render the object correctly, such as colors, reflectance properties, textures, and surface normal. These properties are used in rendering by a vertex shader, part of the vertex pipeline.
Don’t Miss: What Is Chemistry Concept Review Answers
Vertex Angle Of A Parabola
When we graph a quadratic equation, we get a parabola. The vertex definition of a parabola is the point where exactly it turns which is also called the minimum point. When the parabola, opens down the vertex is called the maximum point. The parabola vertex lies at the axis of symmetry. Look at the image below for reference.
In the standard form, we write the quadratic equation as ax2 + bx + c. In the standard form, the vertex of the parabola is given by:
where D is the discriminant. \
The vertex equation of a parabola is of the form \^2 + k\)
The vertex of the parabola is at the coordinate
Example: Graph of \ = 1 – 2x -3\) is as shown below . Find the vertex of the parabola.
Solution:
The coordinates of the vertex are.
Note that the parabola will open downward is negative), but the vertex has a positive y-coordinate.
Therefore, vertex of the parabola is at \
Number Of Vertices Of A Polyhedron
Any convex polyhedron‘s surface has Euler characteristic
- V ,
where V is the number of vertices, E is the number of edges, and F is the number of faces. This equation is known as Euler’s polyhedron formula. Thus the number of vertices is 2 more than the excess of the number of edges over the number of faces. For example, since a cube has 12 edges and 6 faces, the formula implies that it has eight vertices.
Don’t Miss: What Is Erosion In Geography
Interior And Exterior Angles
In case of a polygon, such as a triangle, quadrilateral, pentagon, hexagon, etc., we have both interior and exterior angles.
- Interior angles are those that lie inside the polygon or a closed shape having sides and angles.
- Exterior angles are formed outside the shape, between any side and line extended from adjacent sides.
For example, an image of a pentagon is given here, representing its interior angles and exterior angles.
Vertex Angle In Solid Shapes
Not just plane shapes, even solid shapes have vertices that are formed where the edges meet. The lines do not intersect each other to form the vertex, however, it is the corners or edges of the solid shape that form the vertex. For example, look at the image of a cube, the corners or the edges of the shape are considered as the vertex making a total of 8 vertices. Vertices sometimes are also indicated as the top or apex of a shape such as triangles and pyramids. This vertex or apex is the top corner above the base of the base. For example, look at the image of a tetrahedron, it has 4 vertices.
To find the vertices in a solid shape, we can use Euler’s formula that is given as:
F + V – E = 2
- F is the number of faces
- V stands for the vertices
- E is the number of edges
Also Check: What Is Radius In Math
Angle Based On Rotation
Based on the direction of measurement or the direction of rotation, angles can be of two types:
- Positive Angles
- Negative Angles
Positive AnglesAn angle measured in the counterclockwise direction is a positive angle. In other words, positive angles are those angles that are rotated from the base in the anti-clockwise direction.
Negative AnglesNegative angles are those angles that are measured in a clockwise direction from the base. In other words, negative angles are those angles that are angles are rotated from the base in the clockwise direction.
What Are Adjacent Angles
Based on our definition and the above examples, we can conclude that all pairs of adjacentangles share two properties: a common vertex and a common side. If they are missingone of these components, then they are not adjacent. We can classify pairs of angles asadjacent or not adjacent by looking for these two properties.
There are many special relationships between pairs of angles. Identifying adjacent angles willhelp you recognize other angle relationships, such as supplementary and complementaryangles.
Recommended Reading: What Does Infrastructure Mean In Geography
Definition Of A Line Segment
A line segment is a segment of a line, or in other words, we can say that a line segment is a line with two endpoints.
For example, The diagram shows a line L and one segment of this line is AB.
In a plane, there can be many lines or line segments.
And, these lines can be divided into a few types based on the relative positioning of a line with another line.
Vertical And Adjacent Angles
When two straight lines intersect at a point, four angles are formed, for example, “A,””B,””C,” and “D” angles.
A pair of angles opposite each other, formed by two intersecting straight lines that form an “X”-like shape, are called vertical angles or opposite angles. The opposite angles are mirror images of one another. The degree of angles will be the same. Those pairs are named first. Since those angles have the same measure of degrees, those angles are considered equal or congruent.
For example, pretend that the letter “X” is an example of those four angles. The top part of the “X” forms a “V” shape, that would be named “angle A.” The degree of that angle is exactly the same as the bottom part of the X, which forms a “^” shape, and that would be called “angle B.” Likewise, the two sides of the “X” form “> ” and “< ” shapes. Those would be angles “C” and “D.” Both C and D would share the same degrees, as they are opposite angles and are congruent.
In this same example, “angle A” and “angle C” and are adjacent to each other, they share an arm or side. Also, in this example, the angles are supplementary, which mean that each of the two angles combined equals 180 degrees . The same can be said of “angle A” and “angle D.”
Recommended Reading: What Is Spur In Geography
Angle Definition In Maths
What is an angle? In Plane Geometry, a figure which is formed by two rays or lines that shares a common endpoint is called an angle. The word angle is derived from the Latin word angulus, which means corner. The two rays are called the sides of an angle, and the common endpoint is called the vertex. The angle that lies in the plane does not have to be in the Euclidean space. In case if the angles are formed by the intersection of two planes in the Euclidean or the other space, the angles are considered dihedral angles. The angle is represented using the symbol . The angle measurement between the two rays can be denoted using the Greek letter , , etc. If the angles are measured from a line, we can find two different types of angles, such as a positive angle and a negative angle.
Positive Angle: If the angle goes in counterclockwise, then it is called a positive angle.
Negative Angle: If the angle goes clockwise direction, then it is called a negative angle.
How to Label the Angles?
There are two different ways to label the angles. They are:
Method 1: Give a name to the angle. Generally, the angle is named using the lower case letter like a, x, etc or by using the Greek Letters alpha , beta , theta , etc.
Method 2: By using the three letters on the shapes, we can define the angle. The middle letter should be the vertex .
For example, ABC is a triangle. To represent the angle A is equal to 60 degrees, we can define it as BAC = 60°
How to Measure the Angle?
What Is An Angle
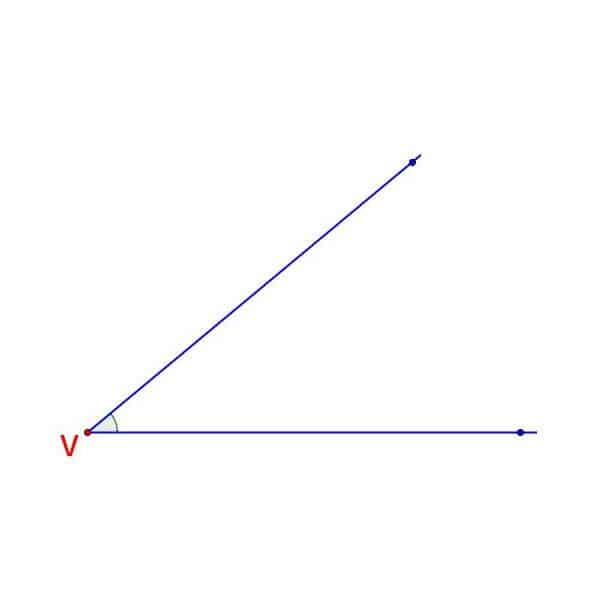
Mathematically, an angle is defined as a figure that forms when two rays meet at a common point. It is represented by the symbol . An angle is usually measured in degrees, denoted with ° . The term angle comes from the Latin word angulus, meaning corner.
A degree is a measure of rotation. A full rotation around a point gives us a full circle which measures 360°, a half rotation gives us a half-circle, which is 180°, and a quarter rotation gives us a right-angle measuring 90°.
You May Like: What Is Cp In Chemistry
Naming Conventions For Angles
The vertex of an angle is the common endpoint of tworays that make up the angle’s sides.
The vertex for angle BAC, written BAC, is point A. The angle can also be named as CAB or by only its vertex, A. When using three points to name the angle, always put the name of the vertex in the middle. So, BAC is not the same angle as ABC or BCA.
Be careful when naming an angle that shares a common vertex with other angles.
BAC above cannot be named by only its vertex since angles CAD and BAD both have A as their vertex. In this case each angle must be named by the points on each side making up the angle and the angle’s vertex.