How Do You Solve For Radius And Diameter
A
If we only know the radius of a circle, well just multiply that value by 2 in order to get the diameter \\). Similarly, if we only know the diameter of a circle, we divide by 2 and out pops the radius \\)!
But, what if we arent given either of these values? In order to solve for either the radius or diameter of a circle, we need to know either its circumference or its area.
Say that we were given the circumference. Since the equation for finding circumference looks like \, well just rearrange the equation and find:\.
If we were given the area, wed rearrange its equation, \, to be: \ Ex.Given that the area of a circle is \, find its diameter.
*We know that the area equation is \, but notice that there is not a diameter variable in this formula. To solve this problem, well either need to: replace \ for r in the area equation, or find the value of r and then multiply that by 2. Here were going to use option b, but both methods are valid choices!
(Notice that the square root of 9 can be either 3 or -3. Since were dealing with a real circle, well simply use
Q
Radius Of Circle From Area
Since, the formula for area of a circle is given by:
Area of circle = 2
Let us see some solved problems on radius and chord of a circle.
Example 1: Find the radius of the circle if its diameter is 16 cm.
Solution:
Diameter of circle = 16 cm
Radius of circle = Diameter/2
= 16/2
= 8 cm
Example 2: If the length of the chord of a circle is 8 cm and the perpendicular distance from the centre to the chord is 3 cm, then what is the radius of the circle?
Solution:
Let us draw a circle as per the given information.
Length of the chord = AB = 8 cm
Perpendicular distance = OP = 3 cm
Radius = OA
We know that, the perpendicular line drawn from the center of a circle to a chord bisects the chord.
AP = PB = 4 cm
OA = 5
Therefore, radius = 5 cm
To know more about the circle, radius of a circle and centre of the circle download BYJUS-The Learning App.
What Is Radius In Simple Words
1 : a straight line extending from the center of a circle to the outside edge or from the center of a sphere to the surface. 2 : an area that extends in all directions from a place Most students live within a radius of five miles from the school. 3 : the bone on the thumb side of the arm between the wrist and the elbow.
Don’t Miss: How To Calculate Half Life Of A Reaction
Example Question #: How To Find The Area Of A Circle
Assume = 3.14
A man would like to put a circular whirlpool in his backyard. He would like the whirlpool to be six feet wide. His backyard is 8 feet long by 7 feet wide. By state regulation, in order to put a whirlpool in a backyard space, the space must be 1.5 times bigger than the pool. Can the man legally install the whirlpool?
Possible Answers:
No, because the area of the backyard is smaller than the area of the whirlpool.
Yes, because the area of the whirlpool is 28.26 square feet and 1.5 times its area would be less than the area of the backyard.
No, because the area of the backyard is 30 square feet and therefore the whirlpool is too big to meet the legal requirement.
No, because the area of the whirlpool is 42.39 square feet and 1.5 times its area would be greater than the area of the backyard.
Yes, because the area of the whirlpool is 18.84 square feet and 1.5 times its area would be less than the area of the backyard.
Correct answer:
Yes, because the area of the whirlpool is 28.26 square feet and 1.5 times its area would be less than the area of the backyard.
If you answered that the whirlpools area is 18.84 feet and therefore fits, you are incorrect because 18.84 is the circumference of the whirlpool, not the area.
If you answered that the area of the whirlpool is 56.52 feet, you multiplied the area of the whirlpool by 1.5 and assumed that that was the correct area, not the legal limit.
When Do Children Learn About The Radius
After learning about 2D and 3D shapes in Years 1 and 2, children will be introduced to the different parts of a circle in Year 6.
Teachers will ask children to measure the radius and diameter of different circles and may also give them string so that they can measure the circumference of the circle.
Recommended Reading: Hrw Com Algebra 1
What Is A Radius
- A radius can be defined as the line from the center O of the circle to the circumference of the circle. It is a line segment represented by the letter R or r.
- A circles radius length remains the same from the middle point to any point on the boundary. A radius is half the length of the diameter of a circle or sphere. So, the radius of the circle or sphere can be expressed as d/2, where d represents the diameter.
- The term radii is the plural of radius, used when talking about the radius of two or more circles.
- A circle can have multiple radii within itself because the circumference of a circle has infinite points. Thus, circles can have an infinite amount of radii, and all of these radii have the same length of distance from the center of the circle.
Formulas for finding the radius of the circle
The radius formula is derived by splitting the diameter of the circle in half. When a point on the circumference of a circle is connected to the exact center, the line segment that appears is called the radius of the ring or circle.
The radius of a circle can be derived using three basic radius formulas, i.e., when the diameter, the circumference, or the area is provided. Given below are the radius formulas for a circle.
Diameter = 2 × radius.
When the diameter of a circle is provided in a problem, the radius formula is written as:
radius = diameter/2 units
= D/2 units.
R= C/2 units
Area of the circle = r2 square units.
Radius = units
Examples:
We know, that area=2R²
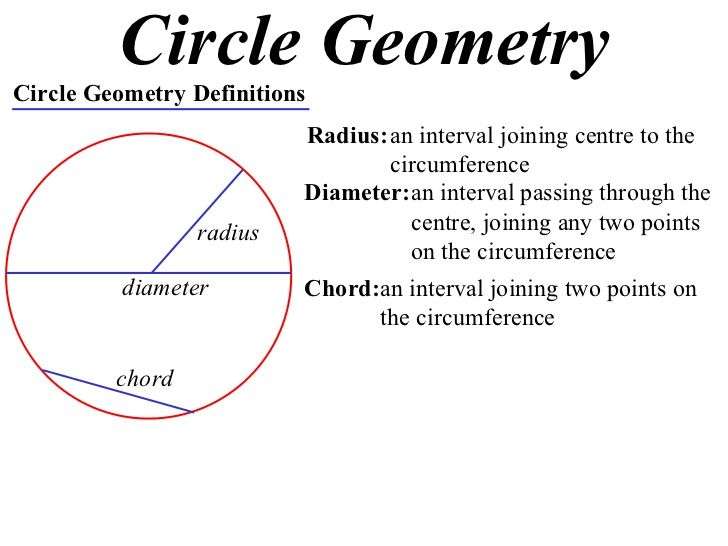
Radius Diameter And Chord
We have already discussed radius and diameter of circle. Now suppose, there is a line and a Circle given on a plane. The line could touch circle at one point, or intersect at two points or it could be non-intersecting.
Explanation:
Given a line and a Circle, it could either be touching the circle, interesting line or non-touching.
Consider any line AB and a circle. Then according to the relative positions of the line and the circle, three possibilities can arise as shown in the given figure.
Line AB intersects the given circle at two distinct points P and Q. The line AB in this case is referred to as secant of the circle. Points P and Q lie on the circumference of the circle, but they do not pass through the center of the circle O, hence line segment PQ is known as a chord of the circle as its endpoints lie on the circle.
Therefore the chord of a circle can be defined as a line segment joining any two distinct points on the circles circumference. A chord passing through the center of a circle is known as the diameter of the circle and it is the largest chord of the circle. This diameter is twice that of the radius of a circle i.e. D=2r, where D is the diameter and r is the radius.
Radius of a circle = Diameter/2Or
Diameter of a circle = 2 x Radius
Read Also: Mm Stands For In Chemistry
Radius Of A Circle Formula
The formula you use depends on what is known about the circle. Below are three different formulas you can use to find the radius, r
| d 2 |
The relationship between radius and diameter is an important one to know when learning to how to calculate the radius.
Since the radius is a line segment from the center to the circle, and the diameter, d , is a line segment from on side of a circle through the center of a circle and out to the other side of the circle, it follows that a radius is 1 a diameter.
How Do I Get The Radius From The Circumference
But suppose you *dont* know the radius of this circle? Suppose all you know is that the circumference is 30 centimeters?
Measuring the circumference of a tree.
One example would be if you were trying to measure a big tree. It would be pretty easy to take a rope and wrap it around the tree, and then measure the length of the rope to find out how big around the tree was , but youd have to cut the tree down to measure the radius.
Read Also: Unit 1 Geometry Basics Segment Addition Postulate
Use In Coordinate Systems
The polar coordinate system is a two–dimensionalcoordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction.
The fixed point is called the pole, and the ray from the pole in the fixed direction is the polar axis. The distance from the pole is called the radial coordinate or radius, and the angle is the angular coordinate, polar angle, or azimuth.
In the cylindrical coordinate system, there is a chosen reference axis and a chosen reference plane perpendicular to that axis. The origin of the system is the point where all three coordinates can be given as zero. This is the intersection between the reference plane and the axis.
The axis is variously called the cylindrical or longitudinal axis, to differentiate it fromthe polar axis, which is the ray that lies in the reference plane, starting at the origin and pointing in the reference direction.
The distance from the axis may be called the radial distance or radius, while the angular coordinate is sometimes referred to as the angular position or as the azimuth.The radius and the azimuth are together called the polar coordinates, as they correspond to a two-dimensional polar coordinate system in the plane through the point, parallel to the reference plane.The third coordinate may be called the height or altitude , longitudinal position,or axial position.
Circumference Of A Circle
For polygons, the perimeter is the sum of the lengths of their sides. Circles have a perimeter, too, but we give it a special word: circumference . The circumference of a circle is the distance around the circle.
Let’s take a look at the ratio of the circumference to diameter in these circles below.
Here is
The distance all the way around C , the circumference of the circle, is 3.1415926 meters.
The circumference of
Set up each circle’s circumference to its diameter. These form ratios. See anything?
The ratio of the circumference C of both circles simplify to the same value, 3.1415926
The ratio of the circumference, C , of any circle to its diameter d is always the same value, 3.1415926 , named using the Greek letter pi , which looks like this: Ï
When using pi, it is acceptable to round to two decimal places.
You May Like: Ccl4 Vsepr Model
Geometry And The Circle
A circle is an important shape in the field of geometry. Let’s look at the definition of a circle and its parts. We will also examine the relationship between the circle and the plane.
A circle is a shape with all points the same distance from its center. A circle is named by its center. Thus, the circle to the right is called circle A since its center is at A. Some real world examples of a circle are a wheel, a dinner plate and a coin.
The distance across a circle through the center is called the diameter. A real-world example of diameter is a 9-inch plate.
The radius of a circle is the distance from the center of a circle to any point on the circle. If you place two end-to-end in a circle, you would have the same length as one diameter. Thus, the diameter of a circle is twice as long as the radius.
We can look at a pizza pie to find real-world examples of diameter and radius. Look at the pizza to the right which has been sliced into 8 equal parts through its center. A radius is formed by making a straight cut from the center to a point on the circle. A straight cut made from a point on the circle, continuing through its center to another point on the circle, is a diameter. As you can see, a circle has many different radii and diameters, each passing through its center.
A plane is a flat surface that extends without end in all directions. In the diagram to the right, Plane P contains points A, B and C.
A circle divides the plane into three parts:
Example 1:
What Is The Radius Formula
The radius of a circle can be calculated through various formulas. Observe the following formulas to calculate the radius:
- When the diameter is known, the formula is Radius = Diameter / 2.
- When the circumference is known, the formula for the radius is Circumference / 2.
- When the area is known, the formula is Radius = .
Also Check: Geometry Dash World All Vault Codes
What Is A Circle
A circle can be defined in many ways.
- It is the collection of all the points in a plane, which lie at a fixed distance from a set point in the plane. The fixed point here is the center, called O.
- It is a closed two-dimensional figure with an area, i.e., the region in a 2D plane bordered by it. It also has a perimeter, which is also called the circumference, i.e., the distance around the circle.
- It is a figure in which all the points in the plane are equidistant from the center, O.
How Do We Use Circumference In Everyday Life
A
The applications of circumference in everyday life are truly endless! One example, though, is determining how large of a tire someone needs for a bike or for a car. Another example would be finding how much wood is in a tree: with a very, very old tree, it would be pretty difficult to measure the diameter of the trees base but itd be straightforward to wrap a rope around the base and measure the circumference. Then, you could use this circumference measurement and reverse-engineer the circumference equation to determine the trees diameter. With this measurement , we could find the volume of wood within this tree. Again, the list of examples could go on and on forever, so keep an eye out for other ways that you use circumference throughout your life!
Q
You May Like: Jonathan Thomas Child Of Rage Now
Radius Of A Circle And Chord
Radius of a circle is the distance from the center of the circle to any point on its circumference. It is usually denoted by R or r. This quantity has importance in almost all circle-related formulas. The area and circumference of a circle are also measured in terms of radius.
| Circumference of circle = 2
Area of circle = 2 |
Radius Of Circle Equation
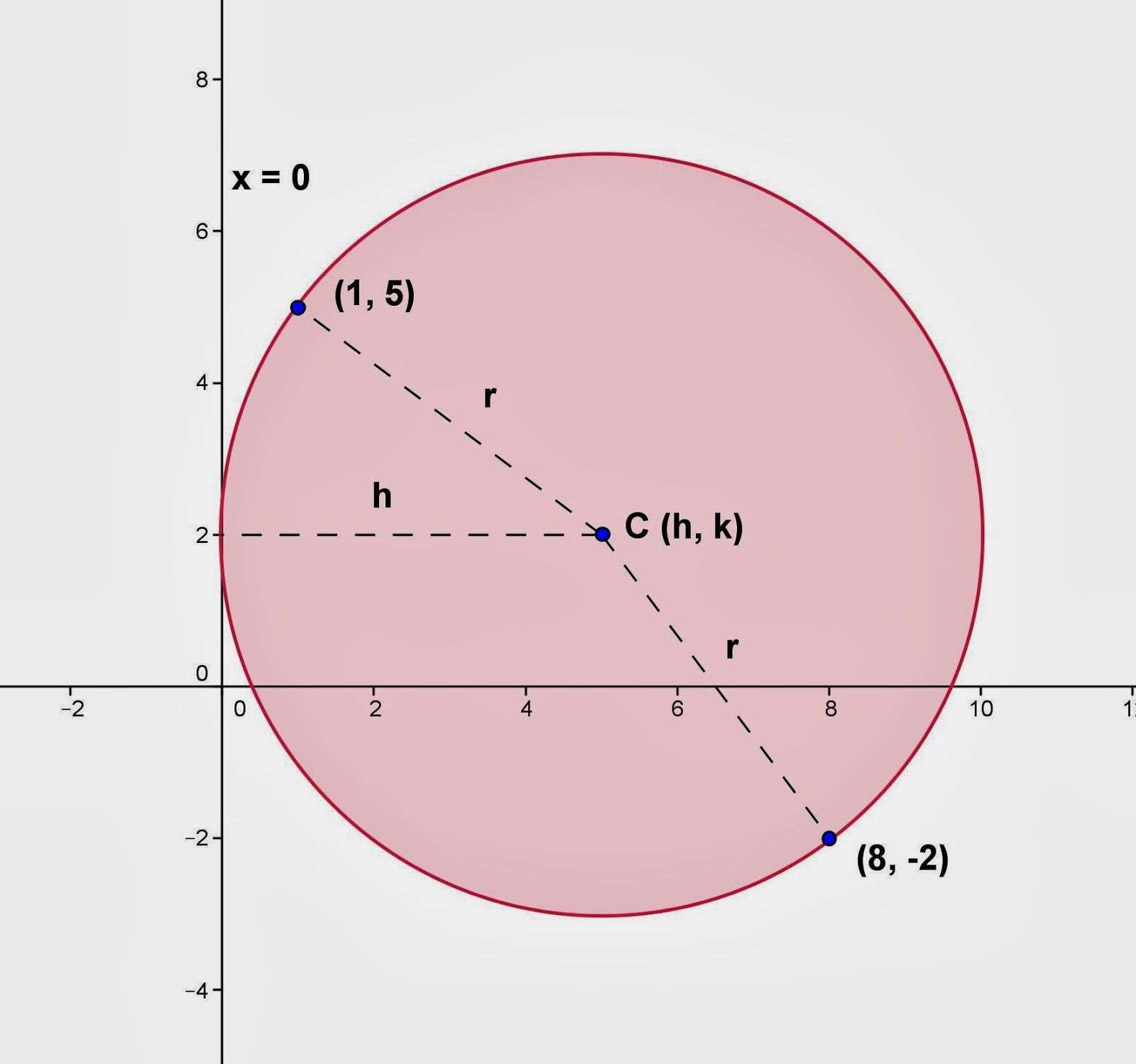
The radius of a circle equation on the cartesian plane with center is given as 2 + 2 = r2. Here, are the points on the circumference of the circle that is at a distance r from the center . When the center of the circle is at origin , the equation of the circle reduces to x2 + y2 = r2. Observe the diagram of a circle on the cartesian plane shown below. Here, the coordinates of the center are and the radius of the circle is represented by ‘r’ joining the center to the point on the circle. So, we just need to substitute these values in the above equation to get the radius of the circle equation. The equation to find the radius of this circle is 2 + 2 = r2 x2 + 2 = r2.
Also Check: Automatic Processes Definition Psychology
How Does Learning Street Help Children With The Radius
Our specialised maths courses will introduce the radius to the child at the same time as they learn about it at school in order to aid their learning. They will be taught about it and then have questions and exercises to practice on in order that they can do it in exams.
Tests could include SATs, competitive 11 Plus tests or selective Independent school exams.
Radius As An Angle Unit
In the study of Trigonometry, the radius of a circle is used to measure an angle with a unit of measure called a radian. If the length of an arc is equal to the length of the radius, the central angle subtended by the arc is 1 radius unit, or 1 radian. Generally, the measure of an angle in radians is some multiple of the length of the radius.
For central angle QPR above, the measure of arc QR is equal to the length of the radius, soQPR = 1 radian.
For central angle QPR above, the measure of arc QR is or about 2.1 times the radius, so radians.
Don’t Miss: Algebra Connections Volume 2 Answers
What Is The Radius Of A Circle
A
If we were to measure the distance running from the center of a circle to the outer edge of said circle, we would be finding the radius. Think of a clock if one of the hands was long enough to reach to the edge of the clock, this hand could be considered the radius of the clock no matter what time it is!
Q