What Does Union Mean In Math

Properties Of Union Of Sets

i) Commutative Law: The union of two or more sets follows the commutative law i.e., if we have two sets A and B then,

AB=BA

Example: A = and B =

So, AB =

BA =

Since, in both the union, the group of elements is same. Therefore, it satisfies commutative law.

A B = B A

ii) Associative Law: The union operation follows the associative law i.e., if we have three sets A, B and C then

C = A

Example: A = and B = and C =

C = =

A = =

Hence, associative law proved.

iii) Identity Law: The union of an empty set with any set A gives the set itself i.e.,

A = A

Suppose, A = and =

then, A = =

iv) Idempotent Law: The union of any set A with itself gives the set A i.e.,

A A = A

Suppose, A =

then A A = = = A

v) Domination Law: The union of a universal set U with its subset A gives the universal set itself.

A U = U

Suppose, A = and U =

then A U = = = U

Hence, proved.

Go through the solved examples given below to understand the concept in a better way.

What Is Set Theory In Maths

As we have already discussed, in mathematics set theory, a set is a collection of different types of objects, and collectively itself is called an object. For example, number 8, 10, 15, 24 are the 4 distinct numbers, but when we put them together, they form a set of 4 elements, such that, .

In the same way, sets are defined in Maths for a different pattern of numbers or elements. Such as, sets could be a collection of odd numbers, even numbers, natural numbers, whole numbers, real or complex numbers and all the set of numbers which comes in the number line.

Set Theory Maths Example

Set theory Maths has numerous applications. Lets imagine youre in a class of 24 students . You want to know the number of males and females in your class. So you begin counting: Males: 1, 2, 3, 12 females: 1, 2, 3, 12 . Set theory can now be used to demonstrate this more clearly.

Here, the letter A represents your class.

As cardinality is 24.

I.e., |A|=24.

So there are 12 males and 12 females, right?

Lets show it off.

Now, F represents all females, while M represents all males.

|F|=12

|M|=12

As a result, the sets are really useful by means of classifying things.

Difference Between Union And Intersection

Categorized under Mathematics & Statistics,Words | Difference Between Union and Intersection

Before understanding the difference between the two set operators union and intersection, lets understand the concept of set theory first. Set theory is a fundamental branch of mathematics that studies sets, particularly whether an object belongs, or does not belong to, a set of objects that are somehow relevant mathematics. Set is basically a collection of well-defined objects, which may or may not be of mathematical relevance, such as numbers or functions. The objects in a set are called elements, which can be anything like numbers, people, cars, states, etc. Almost anything and any number of elements can be collected together to create a set.

In simple terms, set is a collection of any number of unordered elements that can be regarded as a single object as a whole. Lets understand the basic concepts and notation of a set and how it is represented. It all begins with a binary relation between an object x and a set A. To represent if x is a member of a set A, the notation x A is used, while x A indicates that the object x does not belong to the set A. The member of a set are listed within curly braces. For example, the set of prime numbers less than 10 can be written as . Similarly, a set of even numbers less than 10 can be written as . Hypothetically, almost any finite set can be represented by its members.

Don’t Miss: What Is Stroma In Biology

Union And Intersection Examples

1. If X = , and Y = ( Odd Natural Numbers upto 14}. Determine the intersection of two given sets X and Y.

Solution:

Hence, X =

Hence, Y =

Therefore, intersection of X and Y is the largest set including only those elements which are common to both the given sets X and Y.

Hence, X Y =

2. P = and Q = . Find the union of two sets P and Q.

Solution:

P Q =

No elements are repeated in the union of two sets. The common elements i.e. 3 and 7 are considered only once.

Difference Between Union And Intersection Of Sets

AB =

AB =

Don’t Miss: Step By Step Boolean Algebra Simplification Calculator

Union And Intersection Of Sets Cardinal Number Practice Problems

1. Find the Union and Intersection of two sets P and Q Where Set P = and Set Q = . What is the Cardinal Number of P,Q, their union and intersection?

Solution:

Union =

Intersection

Cardinal number of P = Number of elements in P = 7

Cardinal number of Q= Number of elements in Q = 3

Cardinal number of union of two sets = Number of total elements in both the sets = 10

Cardinal number of intersection of two sets= Number of elements in their intersection = 0 .

2. There are a total number of 200 students in Class XI. Among them, 120 students study science, 50 students mathematics, and 30 students study both science and mathematics. Find the number of students who

Solution:

The total number of students denotes the cardinal number of the universal set. Let x represent the set of students studying Science and set Y represent the students studying Mathematics.

Therefore,

The venn diagram denotes the number of students studying both Science and Mathematics.

i. Number of students studying science but not mathematics

Here, we are required to find the difference of sets X and Y.

n = n + n

n = n – n

n = 120 -30

= 90

Hence, the number of students who study Science but not Mathematics are 90.

ii. Number of students studying mathematics but not science.

Here, we are required to find the difference of sets Y and X.

n = n + n

n = n – n

n = 50 -30

= 20

Property Of Universal Set

As per the property of the universal set, the union of the universal set with any set results in the universal set. Mathematically it can be represented as A U = U.

Let’s prove this for A = and U =

then AU = = = U

Related Articles onUnion of Sets

Check out the following pages related to the union of sets

Important Notes on Union of Sets

Here is a list of a few important points related to the union of sets.

• Union of any two sets results in a completely new set that contains the elements that are present in both the initial sets.
• The resultant set contains all elements that are present in the first set, the second set, or elements that are in both sets.
• The union of two disjoint sets results in a set that includes elements of both sets.
• As per the commutative property of the union, the order of the operating sets does not affect the resultant set.
• To determine the cardinal number of the union of sets, use the formula: n = n + n – n

Recommended Reading: Student Projects In Linear Algebra

Intersection Of Two Sets Representation

If X and Y are two sets, then the intersection of two sets is represented by

X Y = n + n – n

Where n is the cardinal number of set X, n is the cardinal number of set Y, n is the cardinal number of union of set X and Y.

To understand the concept of intersection of two sets clearly, let us consider an example.

If Set X = , Set Y = and Set Z = . Find the Intersection of

1. Set X and Y

2. Set Y and Z

3. Set A and C

Solution:

• Intersection of set X and Y is X Y

Set of all the elements which are common to both set X and Y is

• Intersection of set Y and Z is Y Z

Set of all the elements which are common to both set Y and Z is

• Intersection of set X and Z is X Z

Set of all the elements which are common to both set X and Z is

Combining Unions Intersections And Complements

One of the biggest challenges in statistics is deciphering a sentence and turning it into symbols. This can be particularly difficult when there is a sentence that does not have the words “union”, “intersection”, or “complement”, but it does implicitly refer to these words. The best way to become proficient in this skill is to practice, practice, and practice more.

Example \

Consider the following sentence, “If you roll a six sided die, find the probability that it is not even and it is not a 3.” Write this in set notation.

Solution

First, let A be the set of even numbers and B be the set that contains just 3. We can write:

Next, since we want “not even” we need to consider the complement of A:

Similarly since we want “not a 3”, we need to consider the complement of B:

Finally, we notice the key word “and”. Thus, we are asked to find:

Example \

Consider the following sentence, “If you randomly select a person, find the probability that the person is older than 8 or is both younger than 6 and is not younger than 3.” Write this in set notation.

Solution

First, let A be the set of people older than 8, B be the set of people younger than 6, and C be the set of people younger than 3. We can write:

We are asked to find

Notice that the complement of “\” is “\”. Thus:

Next we find:

Finally, we find:

The clearest way to display this union is on a number line. The number line below displays the answer:

Exercise

Read Also: Beginning And Intermediate Algebra 3rd Edition James W Hall

Formula For Number Of Elements In A Union B

Consider two sets, A and B, such that the number of elements in the union of A and B can be calculated as follows.

n = n + n n

Here,

n = Total number of elements in A U B is called the cardinality of a set A U B

n = Number of elements in A is called the cardinality of set A

n = Number of elements in B is called the cardinality of set B

n = The number of elements that are common to both A and B is called the cardinality of set A B, i.e. A intersection B

Learn: Intersection of sets

Basic Mathematical Symbols With Name Meaning And Examples

The basic mathematical symbols used in Maths help us to work with mathematical concepts in a theoretical manner. In simple words, without symbols, we cannot do maths. The mathematical signs and symbols are considered as representative of the value. The basic symbols in maths are used to express mathematical thoughts. The relationship between the sign and the value refers to the fundamental need of mathematics. With the help of symbols, certain concepts and ideas are clearly explained. Here is a list of commonly used mathematical symbols with names and meanings. Also, an example is provided to understand the usage of mathematical symbols.

Also Check: How Did China’s Geography Affect Its Development

How Use Inner Join In Sql

SQL INNER JOIN Keyword

Module : Set Theory And Logic

• Perform the operations of union, intersection, complement, and difference on sets using proper notation.
• Be able to draw and interpret Venn diagrams of set relations and operations.

Commonly, sets interact. For example, you and a new roommate decide to have a house party, and you both invite your circle of friends. At this party, two sets are being combined, though it might turn out that there are some friends that were in both sets.

Also Check: Point Of Tangency Definition Geometry

To Prove A Set Is Empty

To prove a set is empty, use a proof by contradiction with these steps:

Assume not. That, is assume \ is not empty.

This means there is an element is \ by definition of the empty set.

Let \.

Come to a contradition and wrap up the proof.

Prove: \

Proof: Assume not. That is, assume for some set \ \By definition of the empty set, this means there is an element in \

Let \

\ by definition of intersection.

This says \, but the empty set has no elements! This is a contradiction!

Thus, our assumption is false, and the original statement is true.\

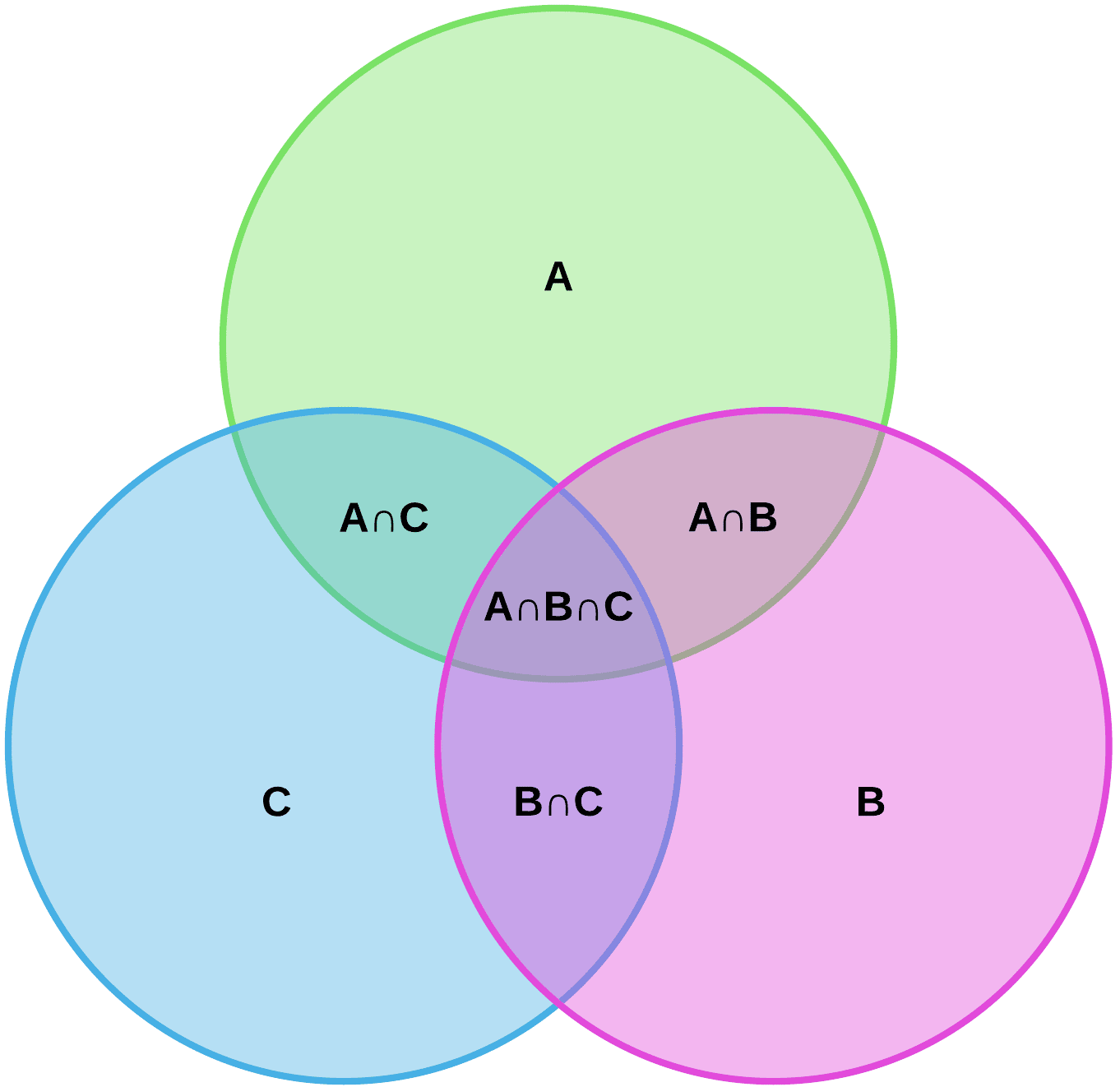
Union And Intersection Venn Diagram

A venn diagram is a diagram that represents the relation between and among a finite group of sets. If we have two or more sets, we can construct a Venn diagram to represent the relationship among these sets as well as the cardinality of sets. Venn diagrams are helpful in representing relationships in statistics,probability, and many more.

Venn diagrams are specifically used in set operation as they give us visual information of the relationship involved.

To learn union and intersection through Venn diagram, we will represent sets with circles as shown below:

Now we will place the values in appropriate places.

The union of set is any region including elements of either A or B

The intersection of sets is any region including the elements of both A and B.

You May Like: Mcdougal Littell Algebra 2 Chapter 2 Test Answers

Union With The Universal Set

For the other extreme, what happens when we examine the union of a set with the universal set? Since the universal set contains every element, we cannot add anything else to this. So the union or any set with the universal set is the universal set.

Again our notation helps us to express this identity in a more compact format. For any set A and the universal set U, A U=U.

Essential Features Of Cantorian Set Theory

At best, the foregoing description presents only an intuitive concept of a set. Essential features of the concept as Cantor understood it include: that a set is a grouping into a single entity of objects of any kind, and that, given an object x and a set A, exactly one of the statements x A and x A is true and the other is false. The definite relation that may or may not exist between an object and a set is called the membership relation.

A further intent of this description is conveyed by what is called the principle of extensiona set is determined by its members rather than by any particular way of describing the set. Thus, sets A and B are equal if and only if every element in A is also in B and every element in B is in A symbolically, x A implies x B and vice versa. There exists, for example, exactly one set the members of which are 2, 3, 5, and 7. It does not matter whether its members are described as prime numbers less than 10 or listed in some order between small braces, possibly .

Also Check: How To Slow Down Biological Aging

Difference Between Union And Intersection Of Set

How Do You Calculate Aub In A Venn Diagram

Summary

Also Check: What Does Synthesis Mean In Biology