Point Of Tangency Definition Geometry

Tangent Applications In Science And Technology

Tangent Lines: Lesson (Geometry Concepts)

Since Tangent is the function of both Sine and Cosine functions, it has a wide range of applications in science and technology. In the field of engineering and physics, trigonometric functions are used everywhere. It is expected to see sine, cos and tan functions in the description, whenever there is something in a circular shape or something that resembles round. Some of the concepts that use trigonometric functions are as follows:

Artificial Neural Networks

Register with BYJUS learning app to get more information about the Maths-related articles and start practice with the problems.

Define Tangent To A Circle

To comprehend the concept of a tangent to a circle, its characteristics, conditions, theorems, and equations, we must first comprehend what a tangent is. Tangent is derived from the Latin word tangere, which means “to touch.” A tangent line is a line or plane that meets a curved line or surface at a single point in geometry. A tangent to a circle is a line that intersects the circle at a single point. The point of tangency is where the tangent meets the circle. The tangent is perpendicular to the circle’s radius, which it crosses.

At the point of contact, the tangent and radius of the circle are perpendicular to one other. How?

Consider the above figure, which shows a circle with O in its centre. The tangent of a circle passing through point R is PQ.
Join OS at a point S on a tangent PQ other than R. Point S should be outside the circle because if it is inside the circle, PQ will be a secant to the circle and not a tangent.
As a result, the OS will be greater than the circle’s radius OR. Except for the point of contact R, this occurs at every point on PQ.
The shortest distance between the centre of circle O and the tangent PQ is determined to be OR.
OR is perpendicular to PQ because the shortest distance between a point and a line is the perpendicular distance between them.

Only one point on the tangent intersects the circle.
The line that contains the radius through the point of contact is referred to as being normal’ to the circle at the point.

Number Of Tangents From A Point On A Circle

Draw a circle on paper. Take a point \ inside the circle. Can a tangent be drawn to the circle through this point \

We see that all the lines through this point \ intersect the circle at two distinct points. So, it is impossible to draw any tangent to a circle from a point inside the circle.

Now, take a point \ on the circle and draw tangents through this point. We observe that only one tangent can be drawn at any point on the circle.

Finally, take a point \ outside the circle and try to draw tangents to the circle from this point. What do we observe? We find that two tangents can be drawn to the circle through this point \

The length of the tangent segment from the external point \ and the point of contact with the circle is called the length of the tangent from the point \ to the circle.

\ and \ are the lengths of the tangents from \ to the circle.

Don’t Miss: Why There Are Different Branches Of Chemistry

What Does The Tangent Ratio Mean

Ans. Two circles in the same plane are internally tangent if their interiors cross in precisely one place and that point is not empty. Two circles in the same plane are outwardly tangent if they cross at a single point and their interiors do not meet.

Ans. A circle has an endless number of tangents.

These lines are known as tangent lines or tangents to the circle from a specific point. Only two tangents can be made from a specific point outside the circle.

Ans. At the point of contact, a tangent to a circle makes a right angle with the circles radius. In addition, if two tangents are drawn on a circle and they intersect, their lengths will be identical.

Ans. A tangent is a line that intersects a circle in exactly one place, and the intersection point is known as the point of tangency. Always, the tangent is perpendicular to the radius traced to the tangency point.

Ans.

Along with cosine and sine ratios, tangent ratios are ratios of two sides of a right triangle. Tangent ratios are the ratio of the side opposite the angle they represent to the side next to the angle. To determine the angle itself, it is necessary to comprehend inverse trigonometric functions.

Can The Two Circles Be Tangent

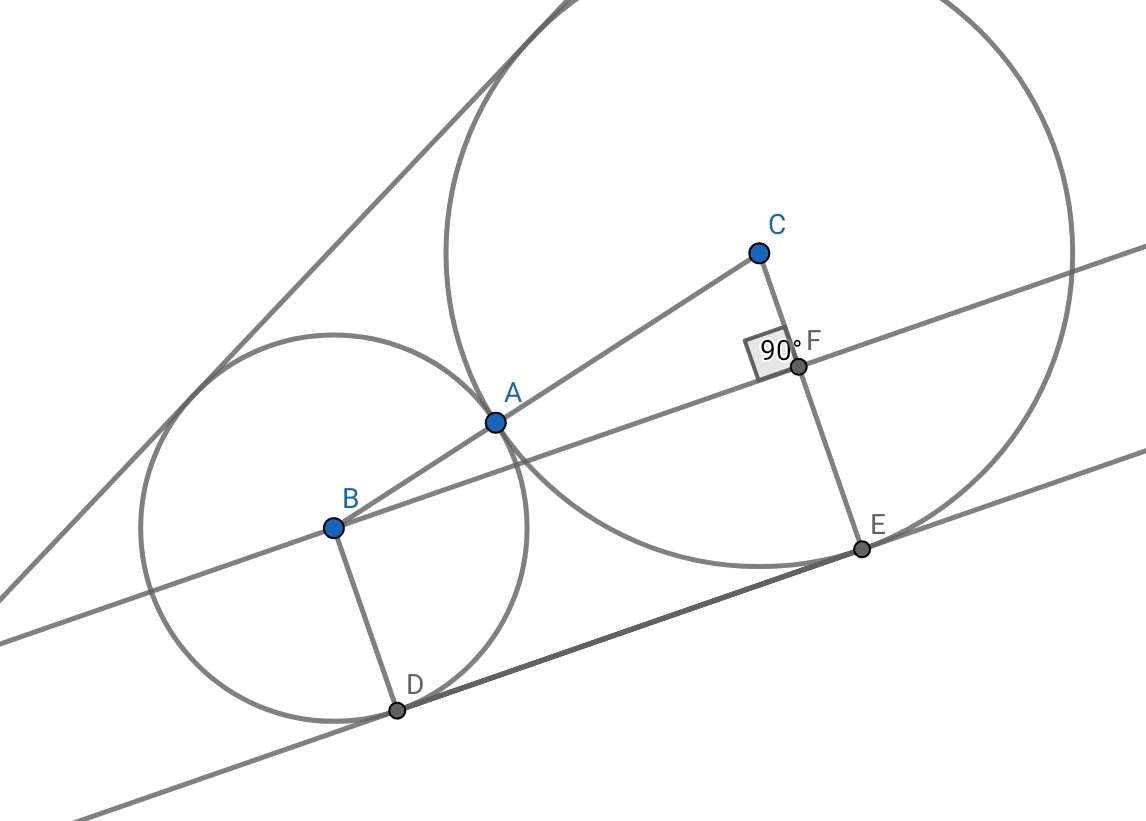
Yes!

The two circles are tangent if they are touching each other at exactly one point. According to the definition of a tangent, it is that touches the circle at exactly one point.

The following diagram is an example of two tangent circles.

Example 1

Find the length of the tangent in the circle shown below.

Solution

The above diagram has one tangent and one secant.

Given us the following lengths:

PQ = 10 cm and QR = 18 cm,

Therefore, PR = PQ + QR = cm

= 28 cm.

Recommended Reading: Example Of Density In Human Geography

Tangent Line Of Parametric Curve In 3d

Let the curve in 3D is defined by the parametric equations x = x, y = y, and z = z. Here are the steps to find the equation of the tangent line at a point t = t0.

Substitute t = a in each of the given equations to find the point at which the tangent is drawn.i.e., = , y, and z)
Find the derivatives x’, y’, and z’.
Substitute t = t0 in each of these derivatives to find the direction ratios < a, b, c> of the line.i.e., < a, b, c> = < x’, y’, z’>
Find the equation of the tangent line using one of the following formulas:x = x0 + at, y = y0 + bt, z = z0 + ct / a = / b = / c

We can see examples of these formulas in the “Examples” section below.

Tangent Of A Circle Definition

A circle is also known as a curve. It is also a closed two-dimensional shape. It is to be observed that the radius of the circle or the line joining the centre O to the point of tangency or the radius of the circle and tangent line are always perpendicular to each other, i.e. OP is perpendicular to XY as shown in the below figure.

Here XY is the tangent of a circle given, and OP is the point of tangency and the tangent radius and the point O represents the centre of the circle.

Thus, the radius and the tangent to a circle are related to each other, tangent to a circle formula that can be well explained using the tangent theorem.

What Is The Tangent To A Circle

The tangent to a circle is defined as a straight line that touches the circle at a single point. The point where the tangent touches a circle is known as the point of tangency or the point of contact.

On the other hand, a secant is an extended chord or a straight line that crosses a circle at two distinct points.

How Tangent Is Important In Real Life

Tangent Properties – Circle Geometry (Tangents from an external point are equal)

It is necessary to study tangents because it allows us to find out the slope of a curved function at a specific point. It is easy to find the slope of a line, but to find out the slope in a curved function, a study of the tangent to a circle is a must. A tangent can be used for different applications such as:

In the differentials and approximations
Architecture
Constructions

Also Check: Geometry Worksheet Answers Mcdougal Littell

Geometry 9 2 Tangents Tangent Definition A Line

Slides: 16

Geometry 9. 2 Tangents

Tangent Definition A line in the plane of a circle that intersects the circle in exactly one point. ta ng en t

Theorem If a line is tangent to a circle, then the line is perpendicular to the radius drawn to the point of tangency.

Converse of the previous Theorem If a line in the plane of a circle is perpendicular to a radius at its outer endpoint, then the line is tangent to the circle.

Corollary Tangents to a circle from a point are congruent.

Exercises A 1. If OC = 15 and OB = 9, then BC = 12 D 3 -4 -5 Triple 15 O 9 C B 2. If OC = 3 6 and BC = 6, then OB = 3 2 3 6 x²+ 6² = ² x²+ 36 = 54 x² = 18 x = 18 = 3 2

Exercises 6. If m< COB = 60 and CB = 6 3, then AB = 12 60 6 3 A D 30 -60 -90 Rt. O C 7. If m< BCD = 70, then m< CBD = m< ____ CDB = 55 70 Iso. B

Answers to Exercises A 3. 4. 5. 8. 10 6 2 8 25 D O C B

Common Tangents A line that is tangent to each of two coplanar circles. common tangent co mm on ta n ge nt

Internal vs. External Tangents A common external tangent does not. common external tangent co A common internal tangent intersects the segment joining the centers of the circle. mm on int er na lt an ge nt

Tangent Circles Two coplanar circles that are tangent to the same line at the same point. There are two types: internally tangent circles externally tangent circles

Homework pg. 335 WE #1 -6, 8 -10, 14 -18

How Do You Find The Point Of Tangency Of A Circle

Hi A point of contact between a tangent and a circle is the only point touching the circle by this line The point can be found either by : equating the equations The line : y = mx +c The circle : ^2 + ^2 = r^2 The result will be the value of which can be substituted in the equation of the line to find

Don’t Miss: What Does Percent Error Mean In Chemistry

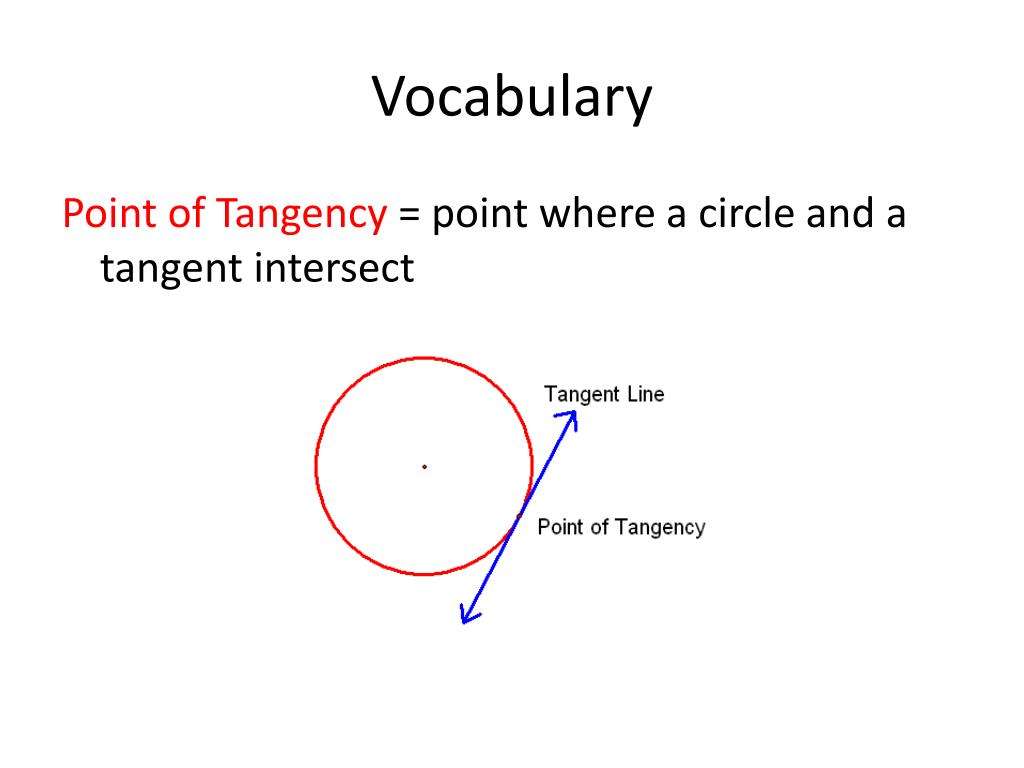
What Is Tangent Line

The tangent line of a curve at a given point is a line that just touches the curve at that point. The tangent line in calculus may touch the curve at any other point and it also may cross the graph at some other point as well. The point at which the tangent is drawn is known as the “point of tangency”. We can see the tangent of a circle drawn here.

If a line passes through two points of the curve but it doesn’t touch the curve at either of the points then it is NOT a tangent line of the curve at each of the two points. In that case, the line is called a secant line. Here, we can see some examples of tangent lines and secant lines. The following shows a secant line PQ but which is NOT a tangent either at P or at Q.

Advanced Information About Circles

A line that intersects a circle in exactly one point is called a tangent and the point where the intersection occurs is called the point of tangency. The tangent is always perpendicular to the radius drawn to the point of tangency.

A secant is a line that intersects a circle in exactly two points.

When a tangent and a secant, two secants, or two tangents intersect outside a circle then the measure of the angle formed is one-half the positive difference of the measures of the intercepted arcs.

$$m\angle A=\frac$$

When two chords intersect inside a circle, then the measures of the segments of each chord multiplied with each other is equal to the product from the other chord:

$$AB\cdot EB=CE\cdot ED$$

If two secants are drawn to a circle from one exterior point, then the product of the external segment and the total length of each secant are equal:

$$AB\cdot AD=AC\cdot AE$$

If one secant and one tangent are drawn to a circle from one exterior point, then the square of the length of the tangent is equal to the product of the external secant segment and the total length of the secant:

$$AB^=AC\cdot AD$$

If we have a circle drawn in a coordinate plane, with the center in and the radius r then we could always describe the circle with the following equation:

$$^+^=r^$$

Read Also: Renate Blauel Children

English Books Relating To The Point Of Tangency

the point of tangencythe point of tangencythe point of tangency2008the point oftangency2008the point oftangency2008thethe point of tangencythe point of tangency2011ofthe point of tangency1996Theofthe point of tangency2002The point of tangencythe point of tangency2011the point of tangency2008ofofthethe point of tangency1859

Derivation Of Value Of Tangent 30 Degrees

As per the properties of a right-angle triangle when its acute angle equals 30, then the length of the hypotenuse is double the length of the opposite side. The length of the adjacent side is 32 times to the length of the measure of the hypotenuse side.

Hence,

Length of Hypotenuse = 2×Length of the measure of the opposite side

Length of Adjacent side= 3/2 × Length of Hypotenuse

Length of Adjacent side= 3/2 ×

Length of Adjacent side= ×Length of Opposite side

Length of Adjacent side=3 × Length of Opposite side

13=Length of opposite side/length of the adjacent side

Since the ratio is tan30,

tan30 = 1/3

Similarly, we can find the values of other angles like 45, 60 using this property of right-angled triangles.

Read Also: Geometry Dash Passwords

How To Find The Tangent Line Equation Of A Parametric Curve In 2d

When the curve is defined by parametric equations x = x and y = y, then the tangent line equation drawn at t = a is found using the steps below:

Find the point = , y).
Find the slope dy/dx using dy/dx = / .
Find the slope of the tangent using m = t = a
Find the equation of the tangent line using y – y0 = m .

Tangent Of A Circle Theorem

Tangent and Point of Tangency Definition

Three theorems are connected to tangents. We already snuck one past you, like so many crop circlemakers skulking along a tangent path: a tangent is perpendicular to a radius.

The second theorem is called the Two Tangent Theorem. It states that, if two tangents of the same circle are drawn from a common point outside the circle, the two tangents are congruent.

The Tangent Secant Theorem explains a relationship between a tangent and a secant of the same circle.

With Point I common to both tangent LI and secant EN, we can establish the following equation:

LI^2 = IE * IN

Though it may sound like the sorcery of aliens, that formula means the square of the length of the tangent segment is equal to the product of the secant length beyond the circle times the length of the whole secant.

Recommended Reading: Michael Jackson Kids Biological

What Are The Four Properties Of Tangents To A Circle

The four major properties of a tangent to a circle are listed as follows:

The tangent is a straight line that touches the circle at only one point.
It is perpendicular to the radius at the point of tangency.
It never enters the circle’s interior.
The lengths of two tangents to a circle from the same external point are equal.

Example Of Tangent Line Approximation

Use the tangent line approximation to find the approximate value of 8.1.

Solution

We know that 8 = 2 and 8.1 very close to 8.

So we assume the function to be f = x and the point where the tangent is drawn to be x0 = 8.

Then = = .

The derivative of the function is f ‘ = x-2/3

The slope of the tangent is, m = ), ) = -2/3 = -2/3 = = 1/12

The equation of the tangent line is, y – y0 = m

y – 2 =

y = x/12 – 2/3 + 2

Now, the approximate value of 8.1 can be obtained by substituting x = 8.1 here. Thus,

f /12 + 4/3

8.1 2.008

We can check this with the calculator by finding the cube root of 8.1 and we can see it to be 2.008. This is how the tangent line approximation works.

Tangent Line Of Polar Curve

If the function is defined by polar equation r = r, then the equation of the tangent line at t = a is found by using the following steps:

Find ‘r’ where r = r.
Find the point where the tangent is drawn using = .
Find dy/dx using the formula,\+r \cos } \cos -r \sin }\).
Find the slope of the tangent using, m = t = a.
Find the equation of the tangent line using y – y0 = m .

Important Notes on Tangent Line:

The equation of tangent line of a curve y = f at a point is found using y – y0 = m ,where m = ).
If is the angle made by the tangent line with the positive direction of the x-axis, then its slope is m = tan .
Normal line and tangent line drawn for a curve at a point are perpendicular to each other and hence the slope of the normal = / .
A curve y = f has horizontal tangents at the points where f ‘ = 0 as horizontal tangents are parallel to x-axis.
A curve y = f has vertical tangents at the points where f ‘ is undefined as horizontal tangents are parallel to y-axis.
The tangent line equation is used to find the approximate values of the function in the neighborhood of the point at which the tangent is drawn.

Related Topics:

On Tangents In Geometry Pdf For Exam

The tangent of a circle is known as a line touching circles or an ellipse at only one point. Imagine, when a line touches the curve at P, then this point P is known as the point of tangency. In differential geometry, the tangent equation can be found using the following methods:

So, we know that finding the gradient of the curve is the gradient of the tangent to the curve at any specified point given on the curve. Hence, the tangent equation of the curve y = f is:

to find the derivative of gradient function through the rules of differentiation.
To find the gradient of the tangent, replace the x- coordinate of the given point in the derivative given.
In the straight-line equations slope -point formula, replace the gradient of the tangent and given coordinate point to find out the tangent equation.

You May Like: Why Do People Copy Others