Presentation On Theme: Unit 1: 3
1 Unit 11: 3-Dimensional Geometry
2 3-D Geometry Vocabulary
3 VocabularyVertex The common point where two or more edges of a three-dimensional solid meet. The corners.
4 VocabularyEdge A line segment where two faces of a three-dimensional figure intersect.
5 Face Polygons which bound the surface of a geometric solid.VocabularyFace Polygons which bound the surface of a geometric solid.
6 VocabularyPrism A three dimensional figure that has two congruent and parallel faces that are polygons. The shape is named by the parallel faces.CubeRectangular PrismParallelogram PrismTriangular PrismHexagonal Prism
7 VocabularyCylinder A solid bounded by two parallel closed curves called its bases, in a plane and the surface formed by straight line segments that join the points on each of the closed curves.
8 VocabularyPyramid A polyhedron whose base is a polygon and whose lateral faces are triangles that share a common vertex. The pyramid is named by the shape at the base.Square-Based PyramidTriangle-Based PyramidHexagonal -Based Pyramid
9 VocabularyCone A solid bounded by a region called its base in a plane and the surface formed by straight line segments which join points on the boundary of the base is a fixed point called its vertex, not in the plane containing the base.
10 VocabularySphere A three-dimensional figure with a set of points in space that are equidistance from a fixed point called the center.
Three Dimensional Geometry For Class 12
Three Dimensional Geometry for class 12 covers important topics such as direction cosine and direction ratios of a line joining two points. The notes are prepared as per the latest CBSE syllabus and NCERT curriculum. Students can revise Maths Chapter 12 with the help of notes formulated as per the latest exam pattern. Also, we will discuss here, the equation of lines and planes in space under different conditions, the angle between line and plane, between two lines etc. You need to practice the questions to understand the topic better and based on the formulas as well.
To understand the different types of shapes and figures, this topic has been introduced in Maths. In the real world, almost all the objects are in a three-dimensional shape. For example, there are many objects at home such as a table, chair, bed, kitchen utensils, etc. which have 3D geometry. In our primary classes, we have learned the basics of three-dimension geometry, but in the 12th standard, we will learn the advanced version of it.
Vrification Des Produits Livrs En Version Boite
Il appartient au Client de vérifier létat de lemballage et la conformité à la commande passée du Produit livré en Version Boite. Toute réclamation sur les vices apparents ou sur la non conformité du Produit livré en Version Boite devra être signalée par le Client dans les cinq jours ouvrables à compter de la date de réception du Produit par le Client, en envoyant : soit un courriel à : ventes@cabri.com soit une lettre recommandée avec Avis de Réception à la Société à ladresse suivante : CABRILOG, 6 Place Robert Schuman 38000 GRENOBLE FRANCE. La date du cachet de la Poste fait foi.
A défaut de réclamation effectuée dans le délai précité, les Produits livrés en Version Boite seront réputés conformes et acceptés par le Client.Aucun Produit ne pourra être échangé avant davoir été réexpédié et réceptionné par la Société, en bon état, tel que livré par les soins de la Société. En particulier le Produit ne devra pas avoir été descellé.
Don’t Miss: What Is Uncertainty In Chemistry
A Few Points On Chapter 12 Introduction To Three Dimensional Geometry
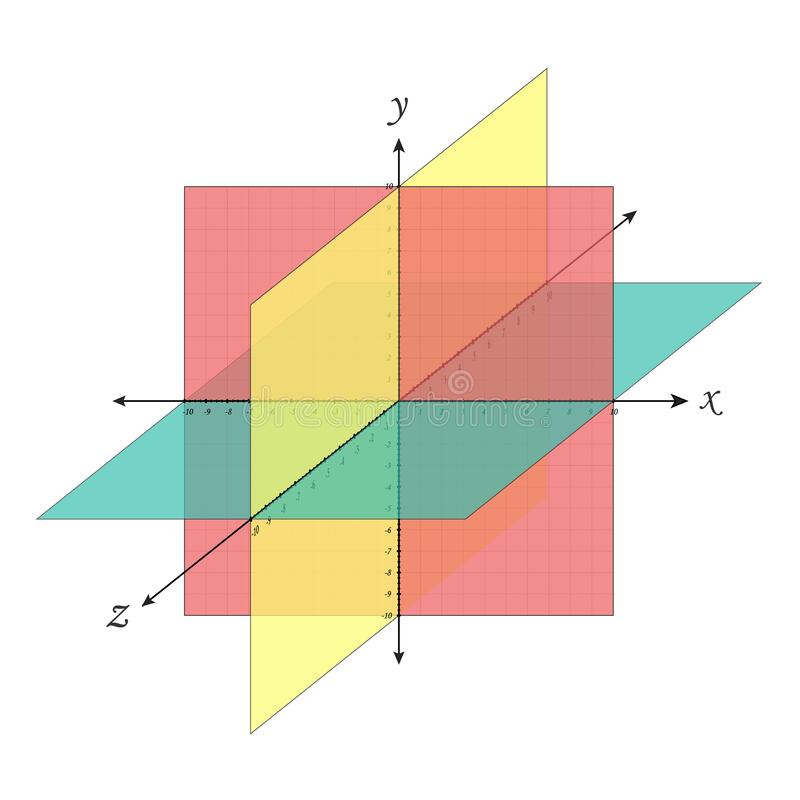
- In three dimensional geometry, a cartesian coordinate system consists of three mutually perpendicular lines namely x, y and z-axes. They are measured in the same unit of length.
- The three planes XY-plane, YZ-plane and ZX-plane are determined by the pair of axes called the axes of the coordinate planes.
- The three coordinate planes divide the space into eight parts known as octants.
- The coordinates of a point P in three-dimensional geometry is written in the form of an ordered triplet. Here x, y and z are the distances from the YZ, ZX and XY-planes.
- Any point on the x-axis is represented as Any point on the y-axis is represented as Any point on the z-axis is represented as .
- The coordinates of the point R divide the line segment joining two points P and Q internally and externally in the ratio m:n.
Subject experts at BYJUS who have prepared the NCERT Solutions for Class 11 Maths have years of understanding about the question paper setting and types of questions that would appear in the second term exam. These solutions provide alternative methods and explanations to solve problems that make the students feel confident while facing the term II exam. Also, solving many complicated problems enhances the Mathematical ability of the students. The solutions cover all the necessary questions, which a student must and should have mastered to appear for the second term exam.
Disclaimer
Ques. 4 and 5 Last Three Points in the Summary
Who Introduced 3d In Geometry
Euclid of AlexandriaAlways remember that unlike two-dimensional shapes, three-dimensional shapes consist of thickness or depth. Question 2: Who invented 3d geometry? Answer: Euclid of Alexandria, who is said to be a student at the Academy by Plato was the one who wrote a treatise in 13 books .
What is a 3D shape PowerPoint?
This is a powerpoint to be used as an introduction or revision of 3D Shapes such as cubes, cuboids, spheres, cylinders etc. It can be used on the interactive whiteboard to lead the lesson and is set up so children can perform practical activities in between slides.
What is 3D geometry?
3D geometry involves the mathematics of shapes in 3D space and involving 3 coordinates which are x-coordinate, y-coordinate and z-coordinate. In a 3d space, three parameters are required to find the exact location of a point.
What is the name of three dimensional geometry?
In mathematics, analytic geometry describes every point in three-dimensional space by means of three coordinates.
Don’t Miss: What Is The Purpose Of Green Chemistry
What Are 3d Shapes
3D shapes are solid shapes or objects that have three dimensions , as opposed to two-dimensional objects which have only a length and a width. Other important terms associated with 3D geometric shapes are faces, edges, and vertices. They have depth and so they occupy some volume. Some 3D shapes have their bases or cross-sections as 2D shapes. For example, a cube has all its faces in the shape of a square. Let us now learn about each 3-dimensional shape in detail. 3D shapes are classified into several categories. Some of them have curved surfaces some are in the shape of pyramids or prisms.
Faqs On Introduction To Three Dimensional Geometry Class 11 Notes Cbse Maths Chapter 12
1. Find the direction cosines of a line that makes angles measuring 90 degrees, 135 degrees, and 45 degrees with the x, y, and z axes, respectively.
Lets assume that the direction cosines of the line are l, m, and n.
In this question, the value of = 90 degrees, = 135 degrees, and = 45 degrees
We also know that l = cos , m = cos , and n = cos
This means that the directions of cosine are:
L = cos 90 = 0
M = cos 135 = cos = -cos 45 = -1 / 2
N = cos 45 = 1 / 2
Hence, the directions cosines of the line are 0, -1 / 2, and 1 / 2
2. Prove that the points , , and are collinear
The lines can also be collinear if the direction ratios of the two line segments are proportional to one another.
This means that if assume that the given points are: A , B , and C , then the direction ratio of the line that is joining the points A and B can be represented by: , , ) =
Here, a1 = -3, b1 = -5, and c1 = -3
The direction ratio of the line that is joining the points B and C is:
Here, a2 = 6, b2 = 10, and c2 = 6
From these equations it should be clear that the direction ratios of AB and BC are of the same proportions. Hence,
A2 / a1 = 6 / -3 = -2
B2 / b1 = 10 / -5 = -2
C2 / c1 = 6 / -3 = -2
This proves that the points A, B, and C are collinear.
3. From where can I download revision notes of Chapter 12 of Class 11 Maths?
Students can download the revision notes of Chapter 12 of Class 11 Maths from Vedantu. They can follow the given steps for the same:
You May Like: Riemannian Geometry Do Carmo Solutions
Direction Ratios Of A Line And Direction Cosine
In this section of the Ch 12 Class 11 Maths Revision Notes, students will be able to learn about the formulas for direction cosine and direction ratios of a line.
For this, lets consider that a line L is passing through the origin. This results in the angle of , , and . This is done with x, y, and z-axes, respectively. Hence, the cosine of these angles is in the direction cosine of the directed line L.
It should also be noted that any three numbers that are proportional to the direction cosines of a line are known as the direction ratios of the line. Hence, the direction cosine of the line L will be l, m, and n. Further, the direction ration a, b, and c will be a = l, b = m, c = n. This is true for non-zero R.
This information can also be depicted as:
L / a = m / b = n / c = k
Also, the value of direction cosine is:
L = ± a / a2 + b2 + c2, m = ± b / a2 + b2 + c2, and n = c / a2 + b2 + c2
You should also keep in mind that if the line is space and does not pass through any origin, then one should draw a line through the origin. This line should be parallel to the given line. This is done while finding the direction of cosines.
After that, you can take one of the directed lines from the origin. This can be done for finding the direction of cosines as two parallel lines have the same set of direction cosines.
-
The Relation Between The Direction Cosines Of A Line
L2 + m2 + n2 = 1
-
Direction Cosines of a Line Passing Through Two Points
Here, PQ = \
Setting Up Powerpoint For Drawing
There are some very powerful tools hidden in the depths of PowerPoint that Microsoft appear to have buried for no particular reason. Lets add them to the quick access toolbar so we can work with ease.
Go to the file menu and click options. Then on the Quick Access Toolbar tab under Choose commands from select All Commands. The picture shows some I have selected at the moment. Merge Shapes is the key one here so add that . I also recommend adding Align, Rotate and Selection Pane…
Also Check: Gina Wilson All Things Algebra Unit 3 Answer Key
D Shapes Faces Edges And Vertices
Let us take an example. The object below is a cube.
The corners of the cube are its vertices. The 12 line segments that form the skeleton of the cube are its edges. The 6 flat square surfaces that are the skin of the cube are its faces. Observe that the two-dimensional figures can be identified as the faces of the three-dimensional shapes. For example, a cylinder has two faces which are circles. Also, a pyramid has a triangle on its face.
| 3D Shapes |
You can download Visualising Solid Shapes Cheat Sheet by clicking on the download button below
Logiciels Garanties Et Obligations
Les logiciels dont la licence dutilisation est vendue sur le Site Internet sont garantis par leur auteur, conformément aux conditions fixées dans leur documentation. La Société ne peut donner aucune garantie quelle quelle soit sur les logiciels et en particulier sur les éventuels défauts ou bogues. Après le complet paiement du prix et sauf clauses contraires plus restrictives figurant sur la licence jointe au Produit, le Client bénéficie sur les logiciels dune licence personnelle dutilisation non cessible pour une durée indéterminée à lexclusion de tout droit de propriété. Conformément aux dispositions légales et réglementaires en vigueur, le Client sinterdit de procéder à toute copie autre que celles autorisées dans le cadre de la législation et à tout acte susceptible de porter atteinte aux droits des auteurs, de leurs ayants droit ou de la Société.
Lutilisation du Produit est subordonnée à lacceptation préalable par le Client, du texte de la licence dutilisation jointe au Produit sous format papier pour la Version Boite et sous forme de fichier électronique pour la Version Electronique.
De convention expresse, linstallation des logiciels sur un matériel info rmatique vaudra acceptation sans réserve de la licence dutilisation jointe.
Also Check: Does Anatomy And Physiology Count As Biology For Medical School
Direction Cosine And Direction Ratios Of A Line
Consider a line L passing through origin makes an angle of , , with x, y, and z-axes respectively, then the cosine of these angles is the direction cosine of the directed line L.
Any three numbers which are proportional to the direction cosines of a line are called the direction ratios of the line. Consider the direction cosine of line L be l, m, n and direction ratio a, b, c then a = l, b = m, c = n, for non-zero R.
Then the direction cosine are:
Note: If the given line in space does not pass through the origin, then, in order to find its direction cosines, we draw a line through the origin and parallel to the given line. Now take one of the directed lines from the origin and find its direction cosines as two parallel line have same set of direction cosines.
What Are The Different Parts Of A 3d Shape

Now Some Technical Terms To Address 3D Shapes Surface. Face. Base. Edge. Corner Vertex /Vertices 6. Surface The curved part of a 3D shape. Eg: Cylinder & Cone Surface 7. Face Part of a 3D shape that is flat. 8. Base The bottom face of a 3D object. Base 9.
Who wrote the elements of geometry?
Around 350 B.C., Euclid of Alexandria wrote The Elements, in which he recorded systematically all that was known about Geometry at that time.
Read Also: How To Use Foil Math
What Objects Are 3d Shapes
The objects that are three-dimensional with length, breadth, and height defined are known as 3D Shapes. A few examples of 3D shapes are a dice which is in the form of a cube, a shoe box which is in the form of a cuboid or rectangular prism, an ice cream cone which is in the form of a cone, a globe which is in the form of a sphere.
What Is The Difference Between Lateral Surface Area And Curved Surface Area Of A 3d Shape
Lateral surface area means the area of all the surfaces of the 3D shape excluding the top and the bottom surfaces. The curved surface area includes the area of only the curved surface in a 3D shape. For example, a cube has 6 flat faces. Its lateral surface area includes the area of all 4 faces excluding the top and the bottom face. A cylinder has two flat faces and one curved surface. So its curved surface area is the area of the curved part between the top and bottom faces which are circular in shape.
Don’t Miss: Geometry Proofs Examples And Answers
Ncert Solutions For Class 11 Maths Chapter 12 Introduction To Three Dimensional Geometry
Given below are the topics of Class 11 Maths Chapter 12 Introduction to Three Dimensional Geometry which is categorized under the second term CBSE Class 11 Maths Syllabus 2022-23.
12.1 Introduction
This section introduces the concept of coordinate axes, coordinate planes in real life, coordinates of the point concerning the three coordinate planes, basics of geometry in three-dimensional space.
12.2 Coordinate Axes and Coordinate Planes in Three Dimensional Space
This section defines the rectangular coordinate system, naming of a coordinate plane and different notations in coordinate planes.
Rahul was riding his bicycle back home from a basketball game from a nearby stadium when he hit the divider to avoid a dog that had run onto the road. Unfortunately, his bicycle was stuck to the divider. When he couldnt remove the bicycle by himself, he decided to take the help of his friend who stayed nearby. Rahul later looked at a topographical map and identified his friends house. He travelled 200 metres south and 550 metres west from where he left his bicycle. The map showed that he had also walked uphill from an altitude of 600 metres to an altitude of 650 metres above sea level. If we treat the location of Rahuls bicycle as the origin of coordinates, what is the position vector of the Kapur farm?
12.3 Coordinates of a Point in Space
This section explains the coordinate system in space, coordinates with few examples.
12.4 Distance between Two Points
12.5 Section Formula
What Is The Difference Between 2d And 3d Shapes
The differences between a 2D shape and a 3D shape are given as follows.
- 2D shapes have a length and a width, whereas, 3D shapes have a length, a width, and a height.
- 2D shapes have an area, they do not occupy any volume, whereas 3D shapes have a surface area and a volume.
- Examples of 2D shapes are triangle, square, rectangle, and examples of 3D shapes are cube, cuboid, prism.
Also Check: What Is Doldrums In Geography