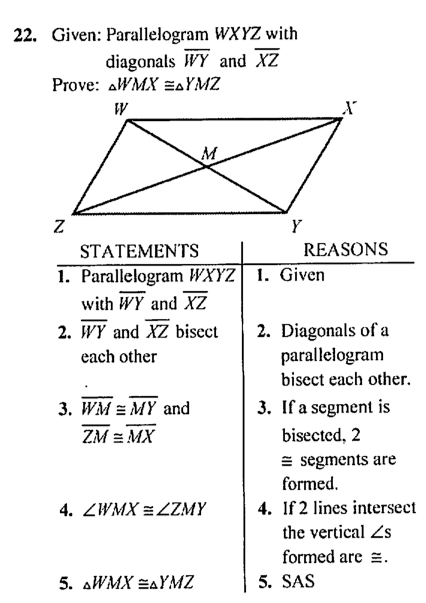
How To Write A Two Column Proof
So what should we keep in mind when tackling two-column proofs?
Always start with the given information and whatever you are asked to prove or show will be the last line in your proof, as highlighted in the above example for steps 1 and 5, respectively.
Remember when you are presented with a word problem its imperative to write down what you know, as it helps to jumpstart your brain and gives you ideas as to where you need to end up?
The same thing is true for proofs.
Start with what you know and this will help to organize your statements and lead you to what you are trying to verify.
Sometimes it is easier to first write down the statements first, and then go back and fill in the reasons after the fact. Other times, you will simply write statements and reasons simultaneously. There is no one-set method for proofs, just as there is no set length or order of the statements.
As long as the statements and reasons make logical sense, and you have provided a reason for every statement, as ck-12 accurately states. As seen in the above example, for every action performed on the left-hand side there is a property provided on the right-hand side. These steps and accompanying reasons make for a successful proof.
Proofs take practice! The more your attempt them, and the more you read and work through examples the better you will become at writing them yourself.
Additionally, its important to know your definitions, , postulates, and theorems.
Pet Peeve To Emphasize:
Ok Ikindaget what you are doing, and each step makes sense, but you are just making it look easy. It seems like you’re just making it up.”“I understand some of where it is coming from, but there is just NO WAY I could come up with these steps myself and get from the beginning to the end on my own.
Posters As A Guide When Stuck:
| To help them organize the procedure and get “un-stuck” when they were unsure how to progress to the next step, I developed a series of steps for them. Some kids really depended on this, and some thought that it didnt help much. For students who do need that structure, this chart is on their desk at ALL TIMES for a month straight. | Another group of students seemed to need a reference list of what kinds of things can be used as justifications. Proofs are so different from anything that has been done before in their math classes. Each student seems to get stuck on a different part of the process. I found that having a reference sheet helped them a lot. |
You May Like: Jonathan Thomas Beth Thomas Brother Now
Mathematics An Example Of Mathematical Proof
A mathematical proof is a process that combines statements weknow to be true to show something else must be true. Basically,it’s just a way of saying something is true, along with why eachstep in the reasoning must be true.
So for example, assume we know “If a< b then a+c< b+c”.Makes sense right? If we add the same thing to both sides, theright side still has more. If we treat this as a fact we know, wecan use it to show other statements must also be true.
Now suppose we want to show that the average of two differentnumbers is between them in value. In other words, if x is thelesser number, then x< /2< y. You might say “that seemslike it would be true”, but you might not be sure it works in everycase .
——
This is how a proof is used. We start with something we know istrue and transform it into somethingelse true. For example, we can start with x < y. We said x isthe lesser number after all.
We then know “x+x< x+y” because of our earlier reasoning “Ifa< b then a+c< b+c”. To avoid proofs being huge, the reasoningis usually just given a name, but the same idea still holds. Inthis case, adding the same number to each side doesn’t change theinequality. Similarly, we can show “x+y< y+y”.
Then we can combine these two to show x+x< x+y< y+y, whichwe rewrite as 2*x< x+y< 2*y. If we divide everything by 2, weget x< /2< y, which is what we wanted to show.
How To Derive The Pythagorean Identities
We can derive the Pythagorean identities using the unit circle. Recall that the unit circle is a circle with a radius of 1. In this triangle, the x-coordinates are represented by and the y-coordinates are represented by as shown in the following diagram:
We see that the legs of the right triangle in the unit circle have the values of and . Also, the hypotenuse of the triangle is the radius of the circle, which is equal to 1. Therefore, using the Pythagorean theorem, we have:
This is the main Pythagorean identity. Using this identity, we can derive two additional identities.
We start with the first Pythagorean identity:
We divide each term by :
Recommended Reading: Holt Mcdougal Pre Algebra Answer Key
Unlock Your Free Trial
Write a direct proof for the following problems.
Problem :
Circle C with triangles ABC and DEC.Chord AB is congruent to chord DE.
Triangles ABC and DEC are congruent.
Problem :
Qaudrilateral DEFG is a parallelogram.
Angles G and E are congruent
Do not use any previously learned theorems. Use the definition of a parallelogram.
Problem :
Segment BD is a median of triangle ABC.Segment DE is a median of triangle ADB.Segment DE is perpendicular to segment AB.
*** Christmas Recipes ***
Italian sausage and a heap of Parmesan cheese lend signature flair to the easy Thanksgiving dressing…
A classic dry martini cocktail made with gin and vermouth and stirred with ice.
It’s all about the layers and ruffles in this dramatic seasonal pie.
As with hot chocolate, use any milky liquid you prefer, whether it’s from a cow, nuts ,…
This is the dramatic seafood paella that looks stunning, with crustaceans and shellfish. You can vary…
Alton Brown’s turkey brine recipe from Good Eats will give you a flavorful Thanksgiving turkey with juicy…
Bone-in turkey breasts are easy to find, and as impressive as a whole bird when you roast them in butter…
Make and share this Basic All Purpose Brine for Meats, Chicken, and Turkey recipe from Food.com.
Cutting leeks into large pieces gives them a presence equal…
Poach quince in rosé with a dash of cocktail bitters and a few warm spices, then assemble into a tart…
It takes a day or two for the peel to dry, so plan ahead perfect Candied Orange Peels
The killer combination of coconut, almonds, and milk chocolate makes for a delectable candy bar. One…
A whole roasted duck doesn’t have to be fussy. With just a few hours’ roasting and hardly any work at…
This recipe is from Eben Freeman, bartender of Tailor Restaurant in New York City. The drink tastes best…
When Beatrice Ojakangas published *The Great Scandinavian Baking Book* in 1988, she won a lot of fans-including…
Read Also: Figure Ground Perception Psychology
Geometry Triangle Proofs Worksheet 2 Answers
Geometry proofs worksheets with answers. Displaying top 8 worksheets found for Beginning Geometric Proofs Answer. Geometry Proofs Easy Displaying top 8 worksheets found for this concept. Then you will need to draw another line on the worksheet and place it at the top of the worksheet.
Geometry 6 3 a worksheet answer key. School number worksheets mom geometric proofs worksheet grade reading games kids constructing quadrilaterals math problems print graph geometry. Access the most comprehensive library of K-8 resources for learning at school and at home.
Proofs coordinate geometry worksheet grade lesson planet. Therefore they have the same length. Some of the worksheets displayed are math aids answer key math aids answer score teacher date perimeter and area of supplementary angles a learning to think mathematically with the ratio table slopeslope intercept form practice representation of integers 1.
Explain using geometry concepts and theorems. Also the answers to most of the proofs can be. Identifying geometry theorems and postulates ANSWERS C congruent.
Showing top 8 worksheets in the category drawing conclusions and making inferences. Displaying top 8 worksheets found for Geometry Proofs Easy. Geometry Proofs Easy Worksheets Learny Kids.
PR and PQ are radii of the circle. P0 P0 _ 9 u VlC _ _ a _yX 9 v. Wednesday 1010 and thursday 1011 review i can review for the test in.
How To Do Proofs In Geometry Lesson & Examples
44 min
- How to Write Two-Column Proofs?
- 00:00:25 What is a two column proof?
- 00:08:58
- Complete the two column proof for congruent segments or complementary angles
- 00:29:19 Write a two column proof
- 00:40:53 List of important geometry theorems
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Recommended Reading: Holt Mcdougal Geometry Worksheet Answer Key
What Is A Proof
A proof is a logical argument that tries to show that a statement is true. In math, and computer science, a proof has to be well thought out and tested before being accepted. But even then, a proof can be discovered to have been wrong. There are many different ways to go about proving something, well discuss 3 methods: direct proof, proof by contradiction, proof by induction. Well talk about what each of these proofs are, when and how theyre used.
Before diving in, well need to explain some terminology.
A theoremis a mathematical statement which is proven to be true.
A statement that has been proven true in order to further help in proving another statement is called a lemma.
Now that weve gotten that out of the way, lets job into some types of proofs!
Congruency Of Triangles: Asa Sss Sas Aas
-
States, if the two angles and the side included between them of one triangle are equal to the two corresponding angles and the side included between them of another triangle, the two triangles are congruent.
-
states, if the three sides of one triangle are equal to the three corresponding sides of another triangle, the two triangles are congruent.
-
says that If two sides and an included angle of one triangle are congruent to two corresponding sides and an included angle of another triangle, then the triangles are congruent.
-
States, if the hypotenuse and side of one right-angled triangle are equal to the hypotenuse and the corresponding side of another right-angled triangle, the two triangles are congruent.
-
says that If two angles and non-included sides of one triangle are congruent to two angles and a non-included side of another triangle, then the triangles are congruent.
You May Like: Kuta Software Infinite Geometry The Segment Addition Postulate Answers
What Are The Pythagorean Identities
Pythagorean identities are equations that contain trigonometric functions, which are true for all substituted values in the variables. Trigonometric identities are especially useful for simplifying trigonometric expressions. The trigonometric identities are derived from the Pythagorean theorem:
This is the most important Pythagorean identity. This identity is true for all values of . Using this first identity, we can create two additional Pythagorean identities:
where, tan represents the tangent function, sec represents the secant function, cot represents the cotangent function, and csc represents the cosecant function.