How To Do Geometry Proofs Step By Step

How To Write A Congruent Triangles Geometry Proof

This article was co-authored by wikiHow Staff. Our trained team of editors and researchers validate articles for accuracy and comprehensiveness. wikiHow’s Content Management Team carefully monitors the work from our editorial staff to ensure that each article is backed by trusted research and meets our high quality standards. This article has been viewed 278,564 times.Learn more…

Congruent triangles are triangles that are identical to each other, having three equal sides and three equal angles.XResearch source Writing a proof to prove that two triangles are congruent is an essential skill in geometry. Since the process depends upon the specific problem and givens, you rarely follow exactly the same process. This can be frustrating however, there is an overall pattern to solving geometric proofs and there are specific guidelines for proving that triangles are congruent. Once you know them, youll be able to prove them on your own with ease.

How To Solve Two

A two-column proof is only a structure, like a skeleton. You must have five tools handy to work your way from premise to conclusion and complete the two column proof:

When You Get Stuck Introduce Part Of What You Are Proving

Sometimes, what you are trying to prove in a geometry proof falls outside of the knowledge you can gather from the statements that has been given. By knowing the theorems, postulates, properties and definitions, your student can introduce their own additional givens based on what they already know.

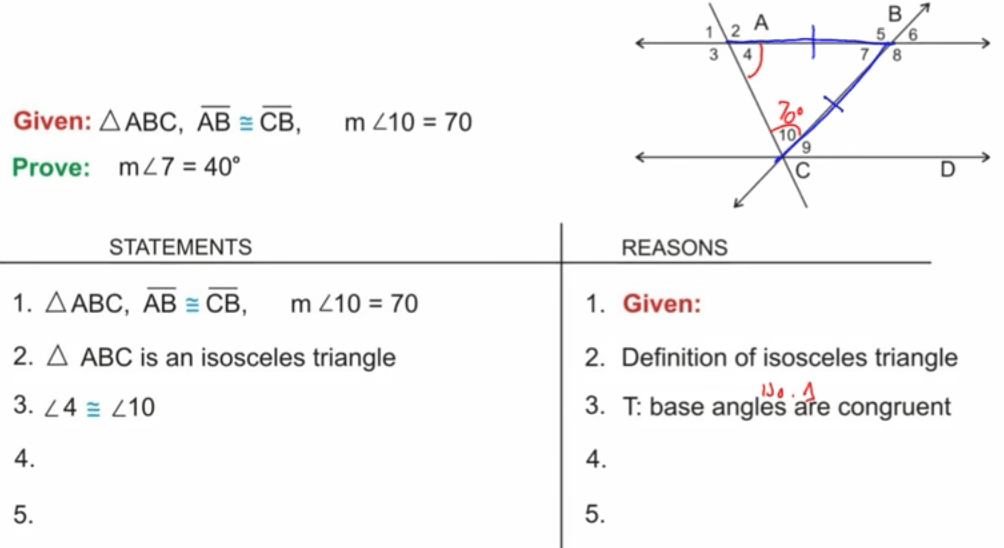
For example, the given statement below does not mention angle 7, which your student is trying to prove.

But, if the given statement helps your student figure out that the triangle is an isosceles triangle, your student can then use what they know about the definition of an isosceles triangle and its angles to figure out the third angle and move to the next step.

This is a great example of using a strong math foundation to solve new problems a skill we often encourage here at Thinkster!

Recommended Reading: Formal Charge Of Cf4

How To Write Two

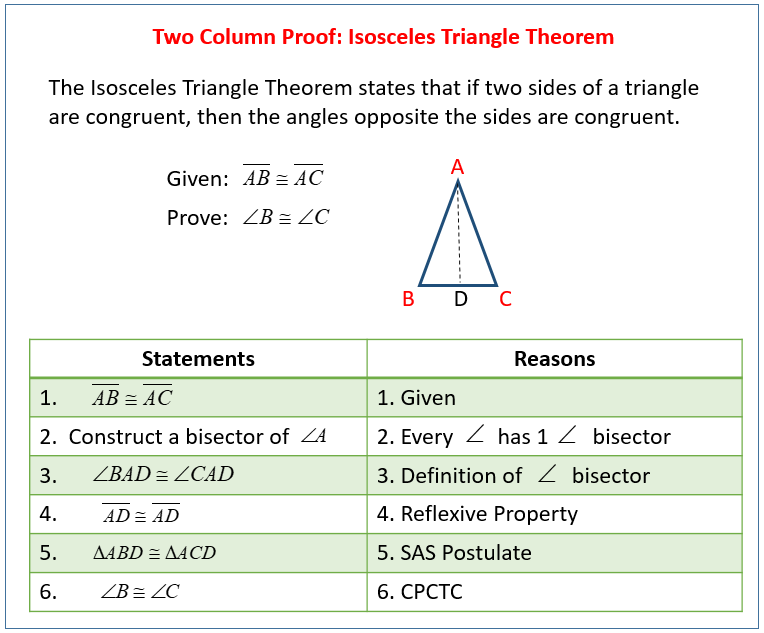
You can write a two-column proof by drawing a horizontal line at the top of a sheet of paper and a vertical line down the middle. Label the left side “Statement” and the right side “Reason.” Say you are asked to prove the Isosceles Triangle Theorem, which states that if two sides of a triangle are congruent, their opposite angles are congruent.

You will be given some information, like WHZ has Side HW Side HZ, making it an isosceles triangle.

You are asked to prove W Z.

Two-column Proof Example

This was a five-step proof. Most geometry proofs can be done in fewer than 10 steps. If you find yourself going past, say, seven or eight steps, you may be going down an inefficient or wrong path. How can you help yourself?

How Would You Break Geometry Proofs Down Into The Necessary Steps

There are a few methodologies , but the three most important ones are practice, practice and practice.

Explanation:

Proof is a set of logical steps that lead you from the given preposition statements to a statement to be proven.In a way, it is like finding a way in a labyrinth from the starting point to the ending point .

One of the most universal methodologies of finding these steps is analysis-based approach.This method starts from the ending point and determines which step might be leading to it. Finding one, we find another step that leads to the step we found. Unraveling this backwards step by step we have to get to the beginning statement given as the premises.

After this process is completed, we should be able to prove our statement by going from the beginning reversing each step as we go until we reach a conclusion.

For example, let’s prove that in an isosceles triangle #Delta ABC#

Read Also: Why Are There Different Branches Of Chemistry

What Does Microsoft Excel Mean

Microsoft Excel is a software program produced by Microsoft that allows users to organize, format and calculate data with formulas using a spreadsheet system.This software is part of the Microsoft Office suite and is compatible with other applications in the Office suite. Like other Microsoft Office products, Microsoft Excel can now be purchased through the cloud on a subscription basis through Office 365.

What Is A Direct Proof

A direct proof is a logical progression of statements that show truth or falsity to a given argument by using:

• Theorems
• Lemmas

In other words, a proof is an argument that convinces others that something is true.

A direct proof begins with an assertion and will end with the statement of what is trying to be proved.

Read Also: Eoc Fsa Warm Ups Algebra 1 Answers

How Can You Resize The Column

To resize the column, you should change the width of one column and then drag the boundary on the right side of the column heading till the width you want. The other way of doing it is to select the Format from the home tab, and in Format you have to select AUTOFIT COLUMN WIDTH under cell section. On clicking on this, the cell size will get formatted.

Lets Be Real: Geometry Can Be Hard

For some students, their problem with understanding geometry could be inherent in their nature. There is some evidence to suggest

that people tend to either relate to math in a more numbers-driven, arithmetical way or a visual/geometric way.

For those in the first group, reasoning spatially is not as easy as it is for the second group, which makes it harder to learn geometric concepts. But dont give up math skills can quickly be learned and developed over time!

One of the most common of all geometry problems is the two-column proof.

Two-column proofs are dreaded by many students as they require them to not only give factual statements to answer the proof but also require students to provide a reason for every statement that is given.

This added step takes extra time and can be frustrating for many students.

Also Check: Abiotic Science Definition

How To Do Proofs In Geometry Lesson & Examples

44 min

• How to Write Two-Column Proofs?
• 00:00:25 What is a two column proof?
• 00:08:58

• Complete the two column proof for congruent segments or complementary angles
• 00:29:19 Write a two column proof
• 00:40:53 List of important geometry theorems
• Practice Problems with Step-by-Step Solutions
• Chapter Tests with Video Solutions

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Pet Peeve To Emphasize:

Ok Ikindaget what you are doing, and each step makes sense, but you are just making it look easy. It seems like you’re just making it up.”“I understand some of where it is coming from, but there is just NO WAY I could come up with these steps myself and get from the beginning to the end on my own.

Read Also: Ccl4 Lewis Structure

Simple Strategies For Solving Geometric Proofs

When you first start working with these types of problems you can easily get overwhelmed. You will need to be observant and take in all the information that is given to you. Once you fully grasp all the aspects of the battle map or in this case the coordinate plane, you can proceed to make sense of it and explain it to others. Here are some simple steps you can get into the habit of to solve them quicker and more efficiently:

Make a Plan and Outline – The best thing to do is to start by creating a plan for yourself. We would encourage you to start by talking it out or writing a short outline of how you should proceed with the problem. Once you have a brief outline, go over the plan to make sure that you did not leave anything out. The dots should connect from one to another. It is then helpful to plug numbers into those values to make sure that you are on the right path. Things that can help you along the way is to spot reference angles and sides of triangles. You can find most of this information by referring to the information that is given to you.

Practice If-Thens – We will begin to draft proofs based on what is given to us. To see if your assumptions make logical sense run the drafted proofs through if-then logic. Using these conditional statements, you should be able to understand if your proof makes sense. You need the conditional statement to be true.

Posters As A Guide When Stuck:

You May Like: Age World Problems

Example: Is 3n1 A Multiple Of 2

Is that true? Let us find out.

1. Show it is true for n=1

311 = 31 = 2

Yes 2 is a multiple of 2. That was easy.

311 is true

2. Assume it is true for n=k

3k1 is true

Now, prove that 3k+11 is a multiple of 2

3k+1 is also 3×3k

And then split 3× into 2× and 1×

And each of these are multiples of 2

• 2×3k is a multiple of 2
• 3k1 is true

3k+11 is true

DONE!

Did you see how we used the 3k1 case as being true, even though we had not proved it? That is OK, because we are relying on the Domino Effect …

… we are asking if any domino falls will the next one fall?

So we take it as a fact that the “n=k” domino falls , and see if that means the “n=k+1” domino will also fall.

Know How Technical Your Students Teacher Is

Sometimes a mathematics course teacher or the teaching assistant wants to make sure that the statements within the proof solution are symmetrical.

In the example below, the given statement shown in step 1 has SA on the left and TB on the right, but what is being proven has them reversed. If your teacher is very technical, they may want your student to use a symmetric property to switch them around to match what is being proven shown in step 5.

Its also important to write out the reasons in the way that your students teacher prefers. The teacher may want everything written out in the long form or he or she may want your child to use specific symbols and abbreviations.

In this same vein, you dont want to end your proof too early.

You may have been able to prove the first or second aspects of the proof, but many teachers will want their students to show all of the statements and reasons they can use to complete the proof.

For example, to prove that two triangles are congruent, your student may have already been able to show that two of the angles within each triangle are congruent and two sides are equal in length. These are shown in steps 2 and 3 below.

It may be important to take this one step further and actually write out that the sides being equal length also make them congruent, which you can see in step 4:

Keep a Proof Reasons List

Also Check: Volume Physics Formula

Example: Adding Up Odd Numbers

1 + 3 + 5 + … + = n2

1. Show it is true for n=1

1 = 12 is True

2. Assume it is true for n=k

1 + 3 + 5 + … + = k2 is True

Now, prove it is true for “k+1”

1 + 3 + 5 + … + + 1) = 2 ?

We know that 1 + 3 + 5 + … + = k2 , so we can do a replacement for all but the last term:

k2 + 1) = 2

Now expand all terms:

k2 + 2k + 2 1 = k2 + 2k+1

And simplify:

k2 + 2k + 1 = k2 + 2k + 1

They are the same! So it is true.

1 + 3 + 5 + … + 1) = 2 is True

DONE!

Now, here are two more examples for you to practiceon.

Please try them first yourself, then look at our solution below.

How To Give Your Child Geometry Help Teach Proofs Like A Math Tutor

Last Updated on August 31, 2021 by

Geometry is the branch of mathematics concerned with the properties and relations of points, lines, surfaces, solids and higher dimensional analogs. For many students, this proves to be a barrier to math success, and they will often turn to you, the parent, for geometry help.

But this can create its own problems. Even if you excelled at geometry and math as a student, its likely been a while since you have practiced it, and you may not be able to explain it in the way your student was taught in school.

Dont worry if you dont have directed tutoring experience or even remember anything from your math class- thats why we have put together this guide for you so that you can teach geometry proofs to your student as a private math tutor or teacher would. It will also help improve your childs study skills in terms of how to layout proofs according to what the teacher deems necessary.

Taking your student to a specialized math center for a session with a private tutor may not be convenient or available in your area. Thats when you have to take matters into your own hands despite not having any direct tutoring experience.

Recommended Reading: Geometry Segment Addition Postulate Worksheet

The Structure Of A Proof

Geometric proofs can be written in one of two ways: two columns, or a paragraph. A paragraph proof is only a two-column proof written in sentences. However, since it is easier to leave steps out when writing a paragraph proof, we’ll learn the two-column method.

A two-column geometric proof consists of a list of statements, and the reasons that we know those statements are true. The statements are listed in a column on the left, and the reasons for which the statements can be made are listed in the right column. Every step of the proof is a row in the two-column proof.

Writing a proof consists of a few different steps.

Given:

Related Questions And Answers

What is called Theorem?

Is a theorem accepted without proof?

What are the 3 types of proofs?

What is formal proof method?

What is a theorem example?

What is the four step method?

How do you prove in Maths?

Why do we prove theorems?

Why are math proofs so hard?

Are theorems always true?

What is the five step method?

Do postulates need to be proven?

Do axioms Need proof?

• Identify the Problem. Begin by determining the scenario the problem wants you to solve.
• Gather Information. Create a table, list, graph or chart that outlines the information you know, and leave blanks for any information you don’t yet know.
• Create an Equation.

Don’t Miss: Geometry Dash Theory Of Everything

How Does Our Tutoring Process Work

Step 1: Schedule a FREE Consultation call with A Diamond Tutoring Manager

Step 1: Schedule a FREE Consultation call with A Diamond Tutoring Manager

Step 1: Schedule a FREE Consultation call with A Diamond Tutoring Manager

Before we are ready to pair your student with any tutor of ours, we would first like to schedule a call with you to learn more about what your student needs help with. We do this to ensure that we find your student a tutor who will be the best possible match for them.

Best part about it? It’s entirely free!

Step 2: Confirm a suitable tutor and Phone Call

Step 1: Schedule a FREE Consultation call with A Diamond Tutoring Manager

Step 1: Schedule a FREE Consultation call with A Diamond Tutoring Manager

Once we have found you a suitable tutor, our manager will send you their tutor profile and schedule a phone call with them. This call is to learn more about your student and establish a tutoring schedule. After deciding on a start date, our manager will help you access your Diamond Tutoring Portal.

Step 3: Tutoring Begins with First Session!

Step 4: Happy Tutoring and regular progress updates!

Step 4: Happy Tutoring and regular progress updates!

After the scheduled phone call with your tutor, our manager will help you access the Diamond Tutoring Portal. Once you begin tutoring, our manager will always be available for you if you have any questions.

Step 4: Happy Tutoring and regular progress updates!

Step 4: Happy Tutoring and regular progress updates!