How To Find Mass In Physics

How To Calculate Impulse With Mass And Velocity

Center of Mass Physics Problems – Basic Introduction

where, I = Impulse, m = Mass, v = Velocity Change How to Use the Impulse Calculator? The procedure to use the impulse calculator is as follows: Step 1: Enter the mass, change in velocity and x for the unknown in the input field. Step 2: Now click the button Calculate the Unknown to get the impulse value. Step 3: Finally, the impulse on an object will be displayed in the output fiel You can also enter the values of mas s and velocity change of an object to calculate the impulse from the equation J = mv. If you know the force acting on the object, enter the values of force and time change instead. Our impulse and momentum calculator will use the J = Ft formula The Impulse-momentum formula is obtained from the impulse-momentum theorem which states that change in momentum of an object is equal to impulse applied on the object. The formula is given as follows: As the SI unit of impulse and momentum are equal, it is given as Ns=kg.m.s –

The Limitations Of Hookes Law

Its important to stress again that Hookes law doesnt apply to every situation, and to use it effectively youll need to remember the limitations of the law. The spring constant, k, is the gradient of the straight-line portion of the graph of F vs. x in other words, force applied vs. displacement from the equilibrium position.

However, after the limit of proportionality for the material in question, the relationship is no longer a straight-line one, and Hookes law ceases to apply. Similarly, when a material reaches its elastic limit, it wont respond like a spring and will instead be permanently deformed.

Finally, Hookes law assumes an ideal spring. Part of this definition is that the response of the spring is linear, but its also assumed to be massless and frictionless.

These last two limitations are completely unrealistic, but they help you avoid complications resulting from the force of gravity acting on the spring itself and energy loss to friction. This means Hookes law will always be approximate rather than exact even within the limit of proportionality but the deviations usually dont cause a problem unless you need very precise answers.

Impulse With Velocity Calculato

ates the mass flow dependence in the analysis. Isp = Veq / go where Veq is the equivalent velocity, which is equal to the nozzle exit velocity plus the pressure-area term, and g0 is the gravitational acceleration
Check out our physics videos at www.physicseh.com This shows you howtocalculatevelocity, acceleration and kinetic energy using Exce
I’m supposed to be able to calculate all of these things: velocity, acceleration, force, momentum and impulse. However, the physics course I’m taking explains it horribly! I think the formulas are: distance over time= velocity, change in velocity over change in time= accleration, but i don’t know if those are right and can’t find the ones for.

, calculate the specific impulse, exit velocity, mass flow, thrust, and throat area. Consider a rocket engine in which the combustion chamber pressure and temperature are 30 and 3756 K, respectively Similarly, the center of mass velocity at take-off, v to, is then given by: where t 1 is a time point before the jump , and t 2 is the take-off time. Center of mass jump height is purely a function of take-off velocity after take-off When an object is at rest, it has zero momentum and zero mass in motion. So, once again, both variables, mass and velocity, are of equal importance when comparing the momentum of two objects. B. Momentum and Impulse Connection. In the previous sports analogy, we noted that once a team has momentum, it may be hard to stop

You May Like: Eoc Fsa Warm Ups Algebra 1 Answers

Weight And Gravitational Force

When an object is dropped, it accelerates toward the center of Earth. Newtons second law says that a net force on an object is responsible for its acceleration. If air resistance is negligible, the net force on a falling object is the gravitational force, commonly called its weight \overset , or its force due to gravity acting on an object of mass m. Weight can be denoted as a vector because it has a direction down is, by definition, the direction of gravity, and hence, weight is a downward force. The magnitude of weight is denoted as w. Galileo was instrumental in showing that, in the absence of air resistance, all objects fall with the same acceleration g. Using Galileos result and Newtons second law, we can derive an equation for weight.

Consider an object with mass m falling toward Earth. It experiences only the downward force of gravity, which is the weight \overset . Newtons second law says that the magnitude of the net external force on an object is }_}=m\overset. We know that the acceleration of an object due to gravity is \overset, or \overset=\overset . Substituting these into Newtons second law gives us the following equations.

Weight

The gravitational force on a mass is its weight. We can write this in vector form, where \overset is weight and m is mass, as

In scalar form, we can write

Since g=9.80\,}^ on Earth, the weight of a 1.00-kg object on Earth is 9.80 N:

What Is The Formula For Work

How to Calculate Mass: 10 Steps (with Pictures)

Definition: In our daily life work implies an activity resulting in muscular or mental exertion. However, in physics the term work is used in a specific sense involves the displacement of a particle or body under the action of a force. work is said to be done when the point of application of a force moves.Work done in moving a body is equal to the product of force exerted on the body and the distance moved by the body in the direction of force.Work = Force × Distance moved in the direction of force.

The work done by a force on a body depends on two factors Magnitude of the force, and Distance through which the body moves

Unit of WorkWhen a force of 1 newton moves a body through a distance of 1 metre in its own direction, then the work done is known as 1 joule.Work = Force × Displacement1 joule = 1 N × 1 mor 1 J = 1 Nm

Recommended Reading: Elton John Children Biological

Period Of A Simple Harmonic Oscillator

The most basic type of periodic motion is that of a simple harmonic oscillator, which is defined as one which always experiences an acceleration proportional to its distance from the equilibrium position and directed toward the equilibrium position. In the absence of frictional forces, both a pendulum and a mass attached to a spring can be simple harmonic oscillators.

It’s possible to compare the oscillations of a mass on a spring or a pendulum to the motion of a body orbiting with uniform motion in a circular trajectory with radius r. If the angular velocity of the body moving in a circle is , its angular displacement from its starting point at any time t is = t, and the x and y components of its position are x = r cos and y = r sin.

Many oscillators move only in one dimension, and if they move horizontally, the are moving in the x direction. If the amplitude, which is the farthest it moves from its equilibrium position, is A, then the position at any time t is x = A cos. Here is known as the angular frequency, and it’s related to the frequency of oscillation by the equation = 2f. Because f = 1/T, you can write the period of oscillation like this:

How To Calculate Mass

This article was co-authored by Sean Alexander, MS. Sean Alexander is an Academic Tutor specializing in teaching mathematics and physics. Sean is the Owner of Alexander Tutoring, an academic tutoring business that provides personalized studying sessions focused on mathematics and physics. With over 15 years of experience, Sean has worked as a physics and math instructor and tutor for Stanford University, San Francisco State University, and Stanbridge Academy. He holds a BS in Physics from the University of California, Santa Barbara and an MS in Theoretical Physics from San Francisco State University.There are 8 references cited in this article, which can be found at the bottom of the page. This article has been viewed 984,094 times.

Mass is one of the fundamental properties of an object in Physics, and is a measurement of how much matter there is in something. Matter is any substance that you can touch anything that takes up physical space and has volume. Often, mass is related to size, but this isnt a perfect relationship, as objects like a large hot-air balloon often have less mass than a small boulder. To calculate mass, youll first need the density and volume of the object. Read on for details of the formula and to learn about different types of mass across scientific disciplines.

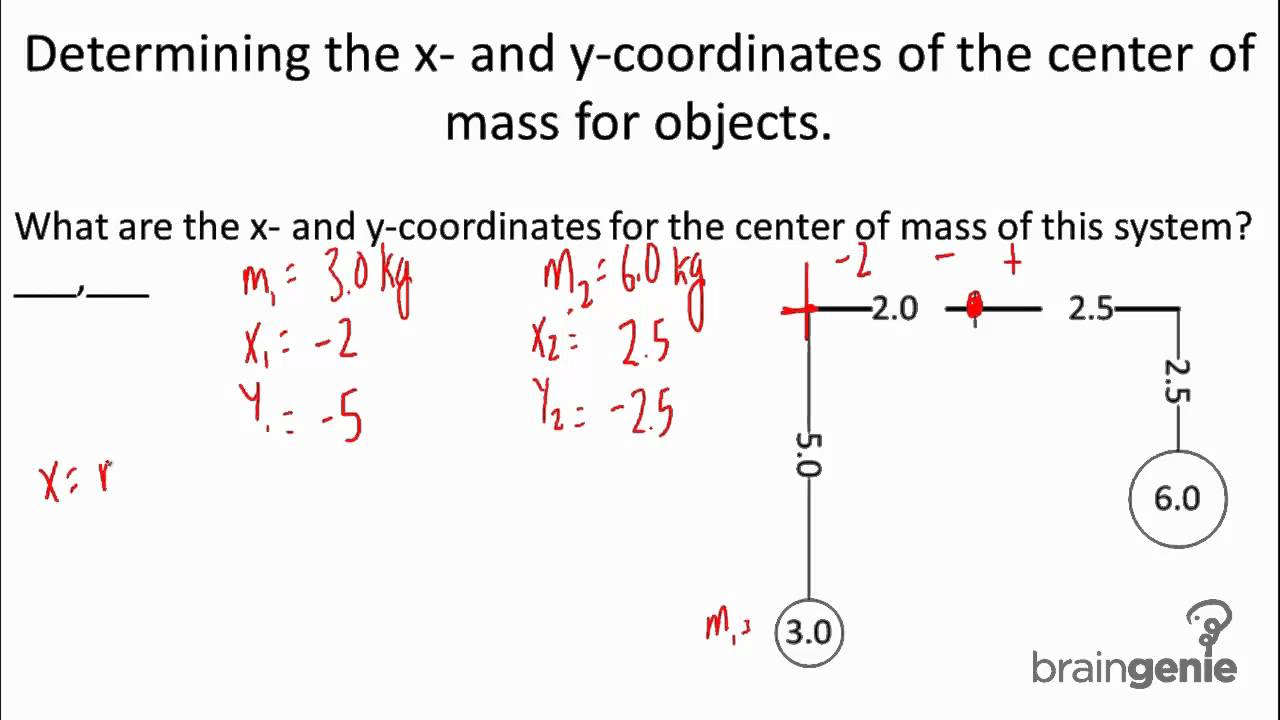
What Is The Center Of Mass

How to Find Speed From Distance & Mass : Math & Physics Lessons

Imagine you want to redecorate your living room and need to move a rolling couch one with extremely well-lubricated wheels from its current position. You decide to push it on its right side as shown in the next image. If you try this, and friction with the floor can be ignored, you will probably notice your couch will rotate instead of just displacing. The resulting movement is represented by the dotted arrows. So, why is the couchs final movement not in a straight line along the direction of the applied force?

Now, imagine you push the couch again but this time right in the center. In this case, there will be no rotation at all, and the couch will move linearly in the same direction of the force, as the following image shows. So what is the difference between this scenario and the first one?

In a lot of physics exercises objects are usually treated as points. We often assume the mass that forms a body to be concentrated in a single point of space, on which all forces act. Now, if the net force applied to that point is not zero, it generates an acceleration in the same direction of said force. This is what Newtons second law of motion indicates:

Fnet=ma

Where m is the objects total mass, and a its resultant acceleration. Nevertheless, when entire objects are considered instead of imaginary points, the result is different. This is because the mass is not concentrated but distributed over the bodys volume. Lets consider this in detail.

Tnet=I

Cx=m2l2m2=l2

Recommended Reading: Geometry Segment Addition Worksheet Answer Key

Shop Our Online Science Store

Solar & Battery Fan DIY STEM Kit

$9.99

Hand-Crank Generator DIY STEM Kit

$9.99

Fan Micro Car DIY STEM Kit

$9.99

3-in-1 Alternative Energy Car DIY STEM Kit

$22.99

Flashing LED Circuit DIY Electronics Kit

$4.99

Line Tracking Car DIY Electronics Kit

$24.99

Solar Micro Car Kit DIY STEM Kit

$7.99

Doodling Shake Bot DIY STEM Kit

$8.99

Impulse And Momentum Calculato

An impulse is simply a change of momentum, and momentum is defined as mass x velocity so you just divide the momentum by the mass to get the velocity. Note about the units: newton x second is the. Impulse is calculated as: a. the product of force and velocity. b. the product of mass times velocity. c. the force divided by the time interval I want to calculate the impulse that is acting on the car during the first 5.78s. If I know that the force on the car steadily increases from 0 N to 3012 N over this time, determine the impulse. If the mass of the car is 1500 kg, also determine the final velocity of the car. Let’s start by graphing the information we were given

Don’t Miss: What Does Vertical Mean In Geometry

How To Calculate The Spring Constant

There are two simple approaches you can use to calculate the spring constant, using either Hookes law, alongside some data about the strength of the restoring force and the displacement of the spring from its equilibrium position, or using the elastic potential energy equation alongside figures for the work done in extending the spring and the displacement of the spring.

Using Hookes law is the simplest approach to finding the value of the spring constant, and you can even obtain the data yourself through a simple setup where you hang a known mass from a spring and record the extension of the spring. Ignoring the minus sign in Hookes law and dividing by the displacement, x, gives:

Using the elastic potential energy formula is a similarly straightforward process, but it doesnt lend itself as well to a simple experiment. However, if you know the elastic potential energy and the displacement, you can calculate it using:

In any case youll end up with a value with units of N/m.

Work Done By A Force Example Problems With Solutions

Example 1: How much work is done by a force of 10N in moving an object through a distance of 1 m in the direction of the force ?Solution: The work done is calculated by using the formula:W = F × SHere, Force F = 10 NAnd, Distance, S = 1 mSo, Work done, W = 10 × 1 J= 10 JThus, the work done is 10 joules

Example 2: Find the work done by a force of 10 N in moving an object through a distance of 2 m.Solution: Work done = Force × Distance movedHere, Force = 10 NWork done, W = 10 N × 2 m= 20 Joule = 20 J

Example 3: Calculate the work done in pushing a cart, through a distance of 100 m against the force of friction equal to 120 N.Solution: Force, F = 120 N Distance, s = 100 mUsing the formula, we haveW = Fs = 120 N × 100 m = 12,000 J

Example 4: A body of mass 5 kg is displaced through a distance of 4m under an acceleration of 3 m/s2. Calculate the work done.Sol. Given: mass, m = 5 kgacceleration, a = 3 m/s2Force acting on the body is given byF = ma = 5 × 3 = 15 NNow, work done is given byW = Fs = 15 N × 4 m = 60 J

Example 5: Calculate the work done in raising a bucket full of water and weighing 200 kg through a height of 5 m. .Solution: Force of gravitymg = 200 × 9.8 = 1960.0 Nh = 5 mWork done, W = mghor W = 1960 × 5 = 9800 J

Example 7: An engine does 64,000 J of work by exerting a force of 8,000 N. Calculate the displacement in the direction of force.Solution: Given W = 64,000 J F = 8,000 NWork done is given by W = Fsor 64000 = 8000 × sor s = 8 m

Recommended Reading: Is Paris Jackson Michael’s Biological Daughter

Calculating The Spring Constant: Basic Example Problems

A spring with a 6 N weight added to it stretches by 30 cm relative to its equilibrium position. What is the spring constant k for the spring?

Tackling this problem is easy provided you think about the information youve been given and convert the displacement into meters before calculating. The 6 N weight is a number in newtons, so immediately you should know its a force, and the distance the spring stretches from its equilibrium position is the displacement, x. So the question tells you that F = 6 N and x = 0.3 m, meaning you can calculate the spring constant as follows:

For another example, imagine you know that 50 J of elastic potential energy is held in a spring that has been compressed 0.5 m from its equilibrium position. What is the spring constant in this case? Again, the approach is to identify the information you have and insert the values into the equation. Here, you can see that PEel = 50 J and x = 0.5 m. So the re-arranged elastic potential energy equation gives:

What Is The Unit Of Mass

There are various units for calculating mass, like, kilograms, grams, lbs, pounds, etc., but the SI unit of mass is “kilograms” or kg. Every unit of mass can be converted to other units by using a proper conversion formula without affecting the meaning and essence of the quantity to be measured.

Note: 1kg is equal to 2.20462 pounds.

Recommended Reading: Who Are Paris Jackson’s Biological Parents

Impulse Formula With Examples

Here, it asks for the impulse, which is a force measured in Newtons, and it is defined as the change in momentum. F=m. We apply this equation for just one of the particles, plug in its mass and initial velocity and final velocity , then take its modulus
Impulse calculator solving for impulse given change in time and force impulse: mass: velocity change: impulse: force: time change: momentum change: mass: velocity change: momentum change: force: time change: References – Books: Tipler, Paul A.. 1995. Physics For Scientists and Engineers. Worth Publishers. 3rd ed
So, we end up with a pretty simple formula that allows us to calculate the vertical jump height if we know the initial velocity. In our specific case we get: This interactive graph shows the relationship between impulse, mass of the jumper, initial velocity and jump height: Calculate Vertical Jump Height based on impulse, velocity and weight
e the final velocity of one of the objects. For example, we know that after the collision, the first object will slow down to 4 m/s. Calculate the momentum of the system before the collision. In this case, initial momentum is equal to 8 kg * 10 m/s + 4 kg * 0 m/s = 80 N·s
g is constant, this may be integrated as follows