Geometry Sin Cos Tan Chart

Trigonometric Ratios In Right Angle Triangle

Trigonometric Ratios are applicable only for a right-angle triangle. A right-angle triangle is a special triangle in which one angle is 90o and the other two are less than 90o. Furthermore, each side of the right angle triangle has a name.

• Hypotenuse: It is the largest side of the triangle. Also, it is opposite the right angle of the triangle.
• Base: The side on which the right angle triangle stands is known as its base. Moreover, any of the two sides other than the hypotenuse can be chosen as the base for performing the calculation.
• Perpendicular: It is the side perpendicular to the base of the right-angled triangle.

You can download Trigonometry Cheat Sheet by clicking on the download button below

Understanding A Unit Circle Chart

When youre dealing with trigonometry, you can use a unit circle diagram. In fact, its one of the best tools which you can use. Rather than making your own unit circle, you can download a unit circle printable and work with it.

Either that or make a blank unit circle to use. If you can understand this concept and what it does, trigonometry will become a lot easier. Youll be able to comprehend it too. Here are some tips to help you out:

Know what a unit circle is

Before you can understand it, you should first know what it is. Actually, a unit circle is simply a circle with a radius of 1 thats centered at the origin. You can use this circle to find special trigonometric functions and ratios.

You can also use it to help you plot graphs. Theres also a number line wrapped around the unit circle. This serves as the input value when youre evaluating trig functions.

Know the 6 basic trig ratios

A unit circle chart has sin cos tan sec csc cot ratios. To understand the chart, you need to know them:

• sin equals opposite/hypotenuse
• cot equals 1/tan.

Know what a radian is

However, you should know how many radians are there in the whole circle. To make things easier for you, a full circle has 2 radians.

Be able to competently convert between degrees and radians

If you want to understand a radian circle chart, you need to be able to convert values competently. In the last point, weve established that a full circle has 2 radians. So here are some quick conversions for you:

Sine Cosine And Tangent

And Sine, Cosine and Tangent are the three main functions in trigonometry.

They are often shortened to sin, cos and tan.

The calculation is simply one side of a right angled triangle divided by another side … we just have to know which sides, and that is where “sohcahtoa” helps. For a triangle with an angle , the functions are calculated this way:

Recommended Reading: What Happened To Beth From Child Of Rage

Tips To Remember Sin Cos Tan Table

The tips that you need to memorize from this chart are:

• The angles 0o, 30o, 45o, 60o, and 90o in order.
• The first row can be remembered like this: 0/2, 1/2, 2/2, 3/2.
• That’s all you need to remember because:The row of cos is as same as the row of sin just in the reverse order.
• Each value in the row of tan is obtained by dividing the corresponding values of sin by cos because tan = sin/cos.

You can see how is tan = sin/cos here:

sin /cos = ÷ = × = Opposite/Adjacent = tan

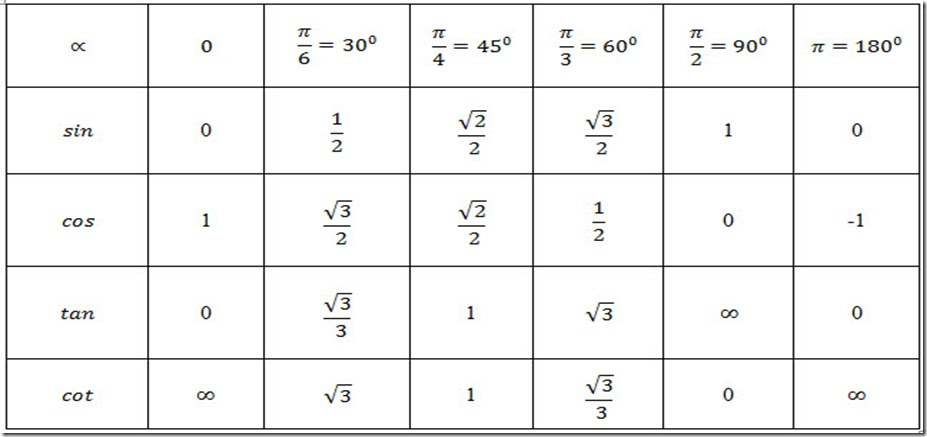
Special Angles: 30 45 And 60

A unit circle shows trig functions clearly because the radius is 1. The hypotenuse doesnt change the value of sin, cos and tan.

The angles 30°, 45°, and 60° have special properties for sin, cos and tan.

A little time spent memorizing them now will save you a LOT of time, doing your working out in the future.

Memorizing sounds like a pain, but dont worry, there are some tricks to help. Lets start with the values for sin.

These are the only values you need to memorize. Can you see why?

Values for cos are the sin-values in reverse!

The final trick is this:

This can be easily remembered by thinking of a stop sign, and cos lettuce. See where this is going?

Tan also leads to a nice pattern, although it doesnt include 0° and 90° like sin and cos do.

Put these all together and you get the table of special trigonometric values, or the unit circle table:

You May Like: What Are 4 Goals Of Psychology

Plot Of The Tangent Function

The Tangent function has a completely different shape … it goes between negative and positive Infinity, crossing through 0, and at every radians , as shown on this plot.

At /2 radians , and at /2 , 3/2 , etc, the function is officially undefined, because it could be positive Infinity or negative Infinity.

What Is The Easiest Way To Learn Trigonometric Tables

To learn the one-hand trick for remembering the trigonometric table easily, designate each finger the standard angles. For filling the sine table we will include counting of the fingers. For the cos table, we will simply fill the values in reverse order.

• Step 1: To find the values of sine functions in a trigonometric table, count the fingers on the left side for the standard angle.
• Step 2: Divide this number of fingers by 4.
• Step 3: Take out the square root of the ratio to find the final sine value.

For example, For sin 0°, there are no fingers on the left-hand side, therefore we will take 0. Dividing the zero by 4 we get 0. Taking the square root of the ratio we would get the value of sin 0° = 0

Similarly, we can find out values for the sine ratio of other angles to fill the table. For tan, divide the value obtained for sin function by the value obtained for cos function.

Don’t Miss: Paris Jackson Mark Lester

What Is Sin Cos Tan In Trigonometry

Sin, cos, and tan are the three primary trigonometric ratios, namely, sine, cosine, and tangent respectively, where each of which gives the ratio of two sides of a right-angled triangle. We know that the longest side of a right-angled triangle is known as the “hypotenuse” and the other two sides are known as the “legs.” That means, in trigonometry, the longest side of a right-angled triangle is still known as the “hypotenuse” but the other two legs are named to be:

• opposite side and
• adjacent side

We decide the “opposite” and “adjacent” sides based upon the angle which we are talking about.

• The “opposite side” or the perpendicular is the side that is just “opposite” to the angle.
• The “adjacent side” or the base is the side that “touches” the angle.

Inverse Of Sine Cosine And Tangent

You can also work out the inverse function to sin, cos and tan, which means 1 divided by that function. They are designated as sin/cos/tan -1. This enables you to work out the angle if you have the sin, cos or tan of it.

In other words:

• Sin1 = 90°

Trigonometry and Calculators

Scientific calculators have sin, cos, and tan functions, as well as inverse functions. Its worth taking a few minutes to work out how your calculator operates, as this could save you hours of messing about when you need it.

Read Also: Algebra Nation Section 1 Test Answers

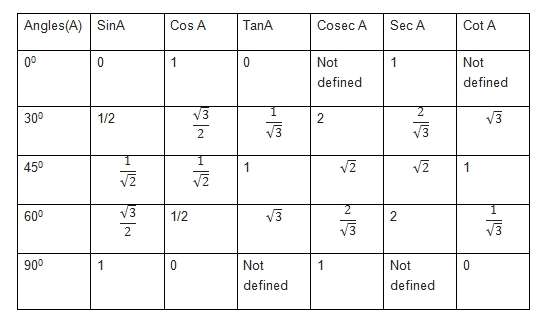
Trigonometry Table For Standard Angles

The trigonometric table is simply a collection of values of trigonometric functions of various standard angles including 0°, 30°, 45°, 60°, 90°, along with with other angles like 180°, 270°, and 360° included, in a tabular format. It is easy to predict the values of the trig ratios in a trigonometric table and to use the table as a reference to calculate trigonometric values for various other angles, due to the patterns existing within trigonometric ratios and even between angles.

The table consists of trigonometric ratios sine, cosine, tangent, cosecant, secant, and cotangent. In short, these ratios are written as sin, cos, tan, cosec, sec, and cot. It is best to remember the values of the trigonometric ratios of these standard angles.

Using the above table, values of sin /6, cos /6, tan /6, sin /4, cos /4, tan /4, sin /3, cos /3, tan /3, sin /2, cos /2, and tan /2 in radians could be easily found out. A trigonometric table has wide application in fields like science and engineering.

A few key points that can be noted in the trigonometric table are,

The Six Main Functions Of An Angle That Are Commonly Used In Trigonometry Are

• sine ,

• secant , and

• cosecant .

An easy and simple way to learn and understand Trigonometry is by studying all the basics of trigonometric angles and formulas by writing them down in a separate notebook which will be really useful to revise them before exams. Make sure you understand and study all the entire right-angle triangle concepts well so that you might compare any problems with a triangle before you try to solve them. The main thumb rule to score well in trigonometry is to learn your Pythagoras theorem with a whole heart. Keeping the Sine rule and Cosine rule at your fingertips will help you solve any type of problem in the examination. Finally, list down all the important identities and formulas of trigonometry in your mind and revision notes as well, and be thorough. Remember to learn how to use the trigonometry table in the necessary place.

1. How can we Convert Cos to Sin?

Since the value of \

Means that if \ is equal to 35 degrees, then \= \ \) = \.

Also \

2. In the given \ABC, right-angled at B and side AB = 24 cm, BC = 7 cm. Find

1. Sin A, Cos A

2. Sin C, Cos C

ABC, right-angled triangle at \ = \ = \

Here it’s given: \ and \

That means, \

According to the Pythagoras Theorem,

The squares of the hypotenuse side are equal to the sum of the squares of the other two sides in a right-angled triangle,

Therefore, \

1. Now for Sin A and Cos A.

Again, the Cosine of an angle is equal to the ratio of the adjacent side and hypotenuse side. Therefore,

Recommended Reading: Unit 1 Geometry Basics Segment Addition Postulate Answer Key

Trig Calculator Finding Sin Cos Tan Cot Sec Csc

To find the trigonometric functions of an angle, enter the chosen angle in degrees or radians. Underneath the calculator, six most popular trig functions will appear – three basic ones: sine, cosine and tangent, and their reciprocals: cosecant, secant and cotangent. Additionally, if the angle is acute, the right triangle will be displayed, which can help you in understanding how the functions may be interpreted.

Alternative Method To Remember

You may prefer this one, because you can figure it out yourself, even in the middle of an exam!

First, you need the tool a special 30-60-90 triangle. There are three steps:

Then, use SOH CAH TOA on the triangle. Remember that each internal angle of an equilateral triangle is 60°, so the halved angle is 30°.

The final piece of the puzzle is which sign to use around the circle, + or -.

Recommended Reading: Punchline Bridge To Algebra Answers

Angles And Sides Of A Triangle

In this section A, B, C denote the three angles of a triangle, and a, b, c denote the lengths of the respective opposite edges. They are related by various formulas, which are named by the trigonometric functions they involve.

Law of sines

The law of sines states that for an arbitrary triangle with sides a, b, and c and angles opposite those sides A, B and C:

In this formula the angle at C is opposite to the side c. This theorem can be proven by dividing the triangle into two right ones and using the Pythagorean theorem.

The law of cosines can be used to determine a side of a triangle if two sides and the angle between them are known. It can also be used to find the cosines of an angle if the lengths of all the sides are known.

Law of tangents

The law of tangents says that:

tan

How To Use Sohcahtoa

Sohcahtoa: SOHCAHTOA is a mnemonic device that is used in mathematics to remember the definitions of the three most common trigonometric functions. This lesson will explain each one and give examples, and youll have the opportunity to take a quiz at the end to solidify what youve learned.

Sine, cosine, and tangent are the three main functions in trigonometry. Theyre all based on ratios obtained from a right triangle. Before we can discuss what ratios work for which function, we need to label the right triangle.

The ratios that allow you to determine the sine, cosine, and tangent of a right triangle are: Opposite is the side opposite the angle in question, adjacent is the side next to the angle in question, and the hypotenuse is the longest side of a right triangle. The hypotenuse is always opposite the right angle.

tangent

You May Like: Algebra 1 Eoc Fsa Practice Test No Calculator Portion Answers

Recap: Trigonometry And Triangles

When we talked about the world of trigonometry, we learned that the part of math called trigonometry deals with triangles. And, in particular, it’s the part of math that deals with figuring out the relationship between the three sides and the three angles that make up every triangle.

Of particular interest to us is the special type of triangles known as right triangles. Every right triangle has one 90-degree angle , and two angles that each range between anything larger than 0 degrees and smaller than 90 degrees .

For our discussion of sine, cosine, and tangent , it’s important that we have a way of labeling the sides of right triangles.

As we learned last time, the longest side of a triangle is known as its “hypotenuse.” The side opposite the angle we’re looking at is known as the “opposite” side . And the side adjacent to the angle we’re looking at is known as the “adjacent” side.

Values Of Trigonometric Ratios At Various Angles:

Trigonometry is a branch of mathematics and a sub-branch in algebra concerned with the measurement of specific functions of angles and their application to calculations. An example of trigonometry which is easy to understand is that of what architects use to calculate any particular distances.

Algebra and trigonometry are two major branches of mathematics. Algebra involves the study of math with specific formulas, rules, equations, and other variables. Trigonometry deals only with the triangles and their measurements.

Recommended Reading: Who Are Paris Jacksons Biological Parents

Definition By Differential Equations

Sine and cosine can be defined as the unique solution to the initial value problem:

d

n . \sin x& =x-}}+}}-}}+\cdots \\& =\sum _^}}x^\\\cos x& =1-}}+}}-}}+\cdots \\& =\sum _^}}x^.\end}}

The radius of convergence of these series is infinite. Therefore, the sine and the cosine can be extended to entire functions , which are complex-valued functions that are defined and holomorphic on the whole complex plane.

Being defined as fractions of entire functions, the other trigonometric functions may be extended to meromorphic functions, that is functions that are holomorphic in the whole complex plane, except some isolated points called poles. Here, the poles are the numbers of the form (

â¡ y \sin z& =\sin x\cosh y+i\cos x\sinh y\\\cos z& =\cos x\cosh y-i\sin x\sinh y\end}}

By taking advantage of domain coloring, it is possible to graph the trigonometric functions as complex-valued functions. Various features unique to the complex functions can be seen from the graph for example, the sine and cosine functions can be seen to be unbounded as the imaginary part of z becomes larger , and the fact that the functions contain simple zeros or poles is apparent from the fact that the hue cycles around each zero or pole exactly once. Comparing these graphs with those of the corresponding Hyperbolic functions highlights the relationships between the two.

Trigonometric functions in the complex plane

Trigonometry Calculator As A Tool For Solving Right Triangle

To find the missing sides or angles of the right triangle, all you need to do is enter the known variables into the trigonometry calculator. You need only two given values in the case of:

• one side and one angle
• two sides
• area and one side

Remember that if you know two angles, it’s not enough to find the sides of the triangle. Two triangles having the same shape may be of different sizes – that kind of relationship is called triangle similarity. If the sides have the same length, then the triangles are congruent.

Don’t Miss: Automatic Processes Definition Psychology

Creating A Unit Circle Chart

Although it may seem confusing, creating a unit circle diagram is quite simple. That is if you have all the steps to do so. Otherwise, you can download a unit circle printable and work with that. Take all the right triangles and the angles of the unit circle. Then put them together, this will create the complete unit circle. As you do this, you need to create special triangles one at a time. You need to do this as they are all specific points on a coordinate plane.

No matter how long the sides you use are for the angle in a triangle, the trig function values would remain the same. To make things easier, mathematicians made all the sides of the triangle smaller.