What Is The Law Of Conservation Of Matter And Energy
The law of conservation of matter and energy states that matter is neither created nor destroyed but conserved. Humans do not have the ability to create or destroy matter or energy. They can only rearrange the matter and energy. For example, an oxygen atom will cycle through a living system.
Mechanical Equivalent Of Heat
A key stage in the development of the modern conservation principle was the demonstration of the mechanical equivalent of heat. The caloric theory maintained that heat could neither be created nor destroyed, whereas conservation of energy entails the contrary principle that heat and mechanical work are interchangeable.
In the middle of the eighteenth century, Mikhail Lomonosov, a Russian scientist, postulated his corpusculo-kinetic theory of heat, which rejected the idea of a caloric. Through the results of empirical studies, Lomonosov came to the conclusion that heat was not transferred through the particles of the caloric fluid.
In 1798, Count Rumford performed measurements of the frictional heat generated in boring cannons, and developed the idea that heat is a form of kinetic energy his measurements refuted caloric theory, but were imprecise enough to leave room for doubt.
The mechanical equivalence principle was first stated in its modern form by the German surgeon in 1842. Mayer reached his conclusion on a voyage to the Dutch East Indies, where he found that his patients’ blood was a deeper red because they were consuming less oxygen, and therefore less energy, to maintain their body temperature in the hotter climate. He discovered that heat and mechanical work were both forms of energy and in 1845, after improving his knowledge of physics, he published a monograph that stated a quantitative relationship between them.
Conservation Laws As Fundamental Laws Of Nature
Conservation laws are fundamental to our understanding of the physical world, in that they describe which processes can or cannot occur in nature. For example, the conservation law of energy states that the total quantity of energy in an isolated system does not change, though it may change form. In general, the total quantity of the property governed by that law remains unchanged during physical processes. With respect to classical physics, conservation laws include conservation of energy, mass , linear momentum, angular momentum, and electric charge. With respect to particle physics, particles cannot be created or destroyed except in pairs, where one is ordinary and the other is an antiparticle. With respect to symmetries and invariance principles, three special conservation laws have been described, associated with inversion or reversal of space, time, and charge.
Conservation laws are considered to be fundamental laws of nature, with broad application in physics, as well as in other fields such as chemistry, biology, geology, and engineering.
Most conservation laws are exact, or absolute, in the sense that they apply to all possible processes. Some conservation laws are partial, in that they hold for some processes but not for others.
Don’t Miss: Holt Mcdougal Geometry Workbook Answer Key
Definition Of A Conservative Force
So exactly what kinds of forces conserve mechanical energy? To answer this we consider particles traveling in closed loops under the influence of the forces in question. In other words, a closed loop describes a “round trip”, during which the particle is under influence of the force. Many systems produce closed loops, such as a ball bouncing up and down, or a mass on a spring. If a conservative force acts upon the particle during this closed loop, the velocity of the particle at the beginning and the end of the loop must be the same. Why? Because if the velocity is any different, the kinetic energy of the particle will be different, meaning that mechanical energy must not have been conserved. Thus we come to our first statement about conservative forces:
If a body is under the action of a force that does no net work during any closed loop, then the force is conservative. If work is done, the force is nonconservative.
In other words, a particle located at the same physical location in a closed loop must have the same kinetic energy at all times if it is within a conservative system. This fact is the fundamental definition of a conservative force. Though we will derive other properties of conservative forces from this statement, it remains the most important one to keep in mind.
Since the work over a closed loop must be zero for conservative forces, what other properties can we state? Let’s break the path of a closed loop into two separate paths:
WWWWWW
What Is Mechanical Energy Definition Facts Types & Examples
There are many forms of energy that exist in nature. But, they all fall into two basic categories. These are kinetic and potential energy. And, when you combine them, what you get is mechanical energy. In other words, by definition, mechanical energy is the sum of kinetic and potential energy.
In this exclusive article, we will talk about the different types of mechanical energy and their real-life examples. What is the energy of motion? What is the energy of position? How to calculate mechanical energy?
More importantly, what is the conservation of mechanical energy? Or, what are the sources of mechanical energy? Not to mention, we will also talk about some of the exclusive facts about mechanical energy. Therefore, I would suggest you stick with me till the end. Lets dive right in!!!
Also Check: Countdown To The Algebra 1 Eoc Answers
Global And Local Conservation Laws
The total amount of some conserved quantity in the universe could remain unchanged if an equal amount were to appear at one point A and simultaneously disappear from another separate point B. For example, an amount of energy could appear on Earth without changing the total amount in the Universe if the same amount of energy were to disappear from a remote region of the Universe. This weak form of “global” conservation is really not a conservation law because it is not Lorentz invariant, so phenomena like the above do not occur in nature. Due to special relativity, if the appearance of the energy at A and disappearance of the energy at B are simultaneous in one inertial reference frame, they will not be simultaneous in other inertial reference frames moving with respect to the first. In a moving frame one will occur before the other either the energy at A will appear before or after the energy at B disappears. In both cases, during the interval energy will not be conserved.
Conservation Of Electric Charge
Electric charge is the property of matter that makes you experience a spark when you touch a metal doorknob after shuffling your feet across a rug. It is also the property that produces lightning and is the basis of all electrical machines and all electrical phenomena in nature, including the behaviors of molecules. Electric charge comes in two varieties, positive and negative. Like charges repel, that is, they tend to push one another apart, and unlike charges attract, that is, they tend to pull one another together. Therefore, two negative charges repel one another and, likewise, two positive charges repel one another. On the other hand, a positive charge will attract a negative charge. The net electric charge on an object is found by adding all the negative charge to all the positive charge residing on the object. Therefore, the net electric charge on an object with an equal amount of positive and negative charge is exactly zero. The more net electric charge an object has, the greater will be the force of attraction or repulsion for another object containing a net electric charge.
Also Check: Ccl4 Vsepr Shape
Conservation Of Linear Momentum
A rocket ship taking off, the recoil of a rifle, and a bank-shot in a pool game are examples that demonstrate the conservation of linear momentum. Linear momentum is defined as the product of an objects mass and its velocity. For example, the linear momentum of a 220 lb football-linebacker traveling at a speed of 10 mph is exactly the same as the momentum of a 110 lb sprinter traveling at 20 mph . Since the velocity is both the speed and direction of an object, the linear momentum is also specified by a certain direction.
the ice, linear momentum is conserved. Throwing an object in one direction will cause you to travel in the opposite direction.
There are many illustrations of the conservation of linear momentum. Begin to walk forward in a rowboat and you will notice that the boat begins to travel backward relative to the water: the momentum your legs impart to your body is equal and opposite to the momentum they impart to the boat. When a rifle is fired, the recoil one feels against ones shoulder is due to the momentum of the rifle, which is equal but in the opposite direction to the momentum of the bullet. Again, since the rifle is so much heavier than the bullet, its velocity is correspondingly less. Conservation of
Examples Of Partial Conservation Laws
The concept of isospin was introduced in the 1930s to describe the similarities of the proton and neutronthey have nearly the same mass and appeared to have the same strong interaction. The proton and neutron came to be regarded as two states of a single underlying particle, the nucleon, to which the mathematics of a spin-½ particle with its two orientations of spin could be applied . Later other particle “multiplets” were found, such as the pion triplet and the xi-particle doublet . The law of isospin conservation states that the strong interaction is identically the same for the members of each multiplet. Isospin conservation is clearly violated by the electromagnetic interaction because particles within a given multiplet don’t have the same charge .
Isospin conservation is now recognized to be a consequence of “flavor invariance.” The six quark flavors are called up, down, charm, strange, top, and bottom flavor invariance means that the strong interactions do not distinguish among flavors. Thus replacing an up quark by a down quark , or even replacing a strange quark by a top quark, does not change any property of the strong interaction. The electroweak interaction does, however, depend on flavor, or quark typethat is, it violates the law of flavor invariance. This is attributed, ultimately, to effects of the Higgs boson.
Read Also: Si Unit For Distance In Physics
What Does Conservation Of Matter Mean
The law of conservation of matter is a fundamental principle of classical physics that states that matter cannot be created nor destroyed in any isolated system, but can only be converted from one form to another. This means that during any chemical or physical change that may occur with any substance, no matter is lost despite the visible changes that are observed.
Types Of Mechanical Energy
Till now, we have already talked a lot about kinetic energy and potential energy. But, as a matter of fact, we dont know what they are!! Or, like how they work? Therefore, without wasting any more time, let me give you a brief review of both of them.
Editors Choice: Top 6 Uniform Motion Examples in SIX minutes
Technically speaking, they are not the type or forms of mechanical energy. In fact, they are just the constituent of mechanical energy. Anyhow, lets move ahead!!!
Recommended Reading: Does Mj Have Any Biological Kids
Application Of Law Of Conservation Of Momentum
Having said so the energy of a system is always conserved, one of the best applications of the law of conservation of momentum would be in space travel, there is no medium in space to exert a force on, then how do rockets travel?
Well, they eject matter at very high speed so in an isolated system the momentum should remain constant therefore the rocket will move in the opposite direction with the same momentum as that of the exhaust.
Stay tuned with BYJUS to know more about the law of conservation of momentum, Newtons Second Law of Motion, and much more.
Derivation Of The Equation Of Motion By Energy Methods

The principle of energy conservation stipulates that the energy is conserved , which gives:
Hence, the derivative of energy with respect to time should be zero. Taking the time derivative of Eq. and equating it to zero gives
Upon performing the differentiation, we get
Simplification by u yields the equation of motion
Min-Hang Bao, in, 2000
Recommended Reading: Who Are Paris Jackson’s Biological Parents
Where To Learn More
Beiser, Arthur. Physics, 5th ed. Reading, MA: Addison-Wesley, 1991.
“Conservation Laws: An Online Physics Textbook” . < http://www.lightandmatter.com/area1book2.html> .
“Conservation Laws: The Most Powerful Laws of Physics” . < http://webug.physics.uiuc.edu/courses/phys150/fall 99/slides/lect07/> .
“Conservation of Energy.” NASA . < http://www.grc.nasa.gov/WWW/K-12/airplane/thermo1f.html> .
Elkana, Yehuda. The Discovery of the Conservation of Energy. With a foreword by I. Bernard Cohen. Cambridge, MA: Harvard University Press, 1974.
“Momentum and Its Conservation” . < http://www.glenbrook.k12.il.us/gbssci/phys/Class/momentum/momtoc.html> .
Rutherford, F. James Gerald Holton and Fletcher G. Watson. Project Physics.New York: Holt, Rinehart, and Winston, 1981.
Suplee, Curt. Everyday Science Explained. Washington, D.C.: National Geographic Society, 1996.
Conservation Of Energy In Beta Decay
The discovery in 1911 that electrons emitted in beta decay have a continuous rather than a discrete spectrum appeared to contradict conservation of energy, under the then-current assumption that beta decay is the simple emission of an electron from a nucleus. This problem was eventually resolved in 1933 by Enrico Fermi who proposed the correct description of beta-decay as the emission of both an electron and an antineutrino, which carries away the apparently missing energy.
Don’t Miss: Does Mj Have Any Biological Kids
The Physical Principle Of Energy Conservation
The impetus for the principle of energy conservation originally is the observation that in simple systems on Earth, one may define an energy of position and connect it to another form of energy, kinetic energy. For a simple mechanical system with no friction, using Newton’s second law , we recast the work as
mv 2 is called the kinetic energy . With this nomenclature, we find from the definition of potential energy that
and rewriting slightly, we obtain
Note that the quantity on the left refers only to position 2, while that on the right refers only to position 1. Since 1 and 2 were completely unspecified, this equation states a general result: in such a simple system, the quantity T+U must be a constant . This is referred to as conservation of mechanical energy .
More generally, the total potential energy is the sum of all the potential energies possible in a given situation. There is no new physics in the principle of conservation of mechanical energy. Everything follows from Newton’s laws .
The relativistic energy relation E2=p2c2+m2c4 may be recast as E=γmc2 for massive objects , where the relativistic momentum is p=γmv and γ / 2 . In this case, the kinetic energy is T=mc2 because T plus mass-energy must be equal to total energy E.
Gustavo Alonso, … Jose Ramon Ramirez, in, 2020
Conservation Of Linear Momentum: Rifles And Rockets
FIRING A RIFLE.
The conservation of linear momentum is reflected in operations as simple as the recoil of a rifle when it is fired, and in those as complex as the propulsion of a rocket through space. In accordance with the conservation of momentum, the momentum of a system must be the same after it undergoes an operation as it was before the process began. Before firing, the momentum of a rifle and bullet is zero, and therefore, the rifle-bullet system must return to that same zero-level of momentum after it is fired. Thus, the momentum of the bullet must be matchedand “cancelled” within the system under studyby a corresponding backward momentum.
When a person shooting a gun pulls the trigger, it releases the bullet, which flies out of the barrel toward the target. The bullet has mass and velocity, and it clearly has momentum but this is only half of the story. At the same time it is fired, the rifle produces a “kick,” or sharp jolt, against the shoulder of the person who fired it. This backward kick, with a velocity in the opposite direction of the bullet’s trajectory, has a momentum exactly the same as that of the bullet itself: hence, momentum is conserved.
ROCKETING THROUGH SPACE.
If, while standing on the ice, one throws an object in one direction, one will be pushed in the opposite direction with a corresponding level of momentum. However, since a person’s mass is presumably greater than that of the object thrown, the rearward velocity will be smaller.
Read Also: Michael Jackson Kids Biological
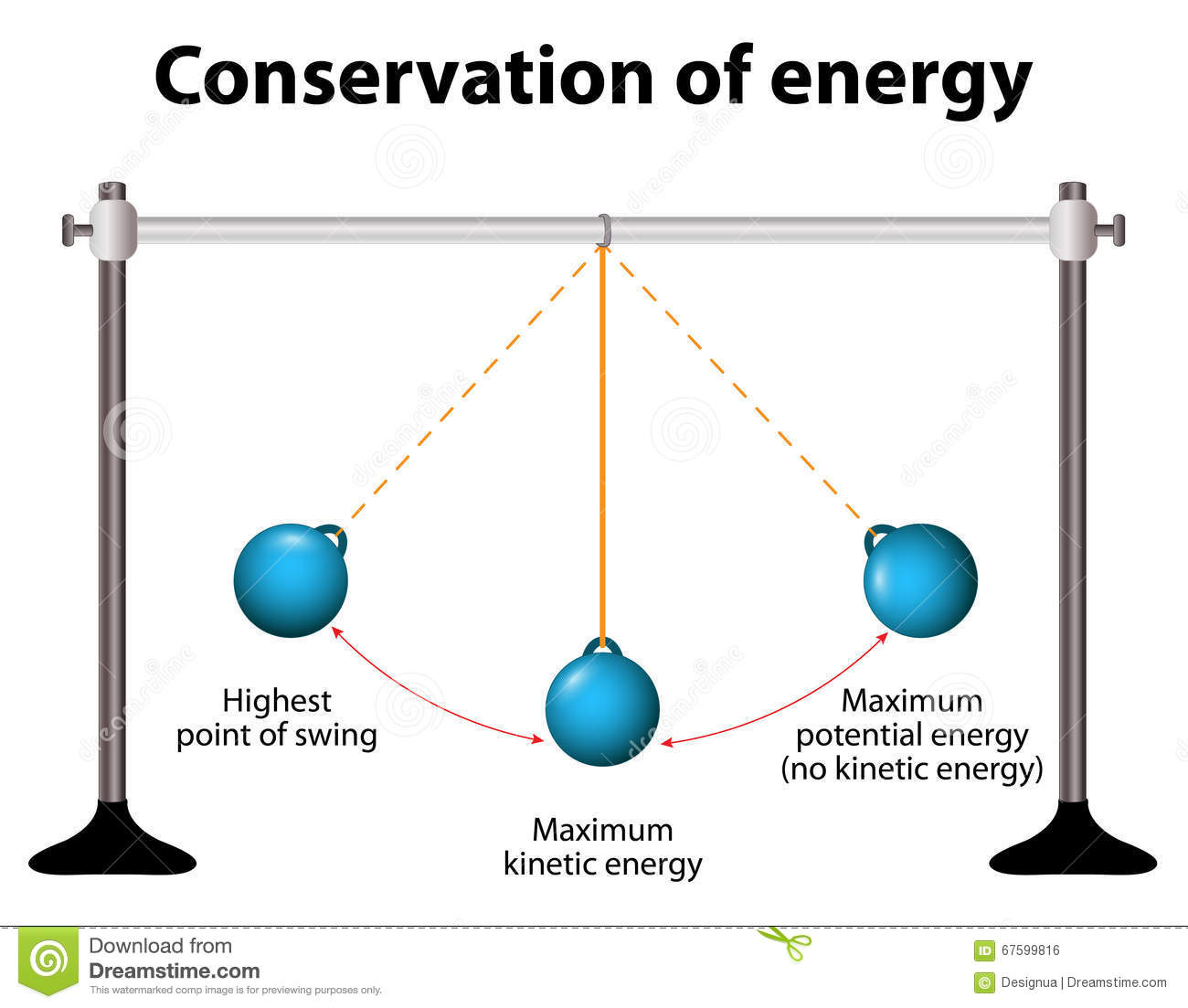
Conservation Of Mechanical Energy
According to the law of conservation of mechanical energy definition, energy can neither be created nor be destroyed, until or unless some kind of external forces like frictional forces or non-conservative forces are applied.
In other words, the total mechanical energy of a system is conserved. Therefore, energy can only convert from one form to another form of energy.
YEAH YEAH, you would be thinking that the above-mentioned definition is of the law of conservation of energy i.e the first law of thermodynamics.
The author of the article must be lying and all. Well, let me clear the air. Neither I am lying, nor you are wrong. In fact, we both are correct. Confused????
Okay, lets take an example to understand it properly. Not to mention, there can be so many examples to explain the concept of the conservation of mechanical energy. Out of all, I am going to explain the most generic one. Keep reading!!!
Conservation Of Momentum Equation
The general equation for conservation of momentum during a collision between n number of objects is given as:
Where mi is the mass of object i, via is the velocity of object i before the collision, and vib is the velocity of object i after the collision.
This formula is given in summation notation, which makes it easy to equate the sum of all objects momentum before the collision to the sum of all objects momentum after the collision.
Recommended Reading: Holt Geometry Lesson 4.5 Practice B Answers