The Goal Of Principal Component Analysis
It is important to first have a vague sense of what PCA is trying to achieve.
It is trying to reduce the dimensionality of the input data. But what does this mean? Lets take a specific example. Say we have two roughly correlated features, collected from a mass survey of Canadian citizens: personal happiness and personal achievement.
As we can see, these two features are highly correlated people with high personal achievement are likely to be happier, and vice versa.
Lets say that these two features are just a segment of a much larger dataset with many, many more features associated with the answers to different questions on the survey. Say we have so much data that our data analysis technology is starting to falter, and we want to see ways in which we can reduce the size of our dataset.
Looking over the graphs of all sorts of questions, we see that personal happiness and personal achievement are highly correlated. We could save a lot of space if we could combine these two features into one feature, something like personal contentedness.
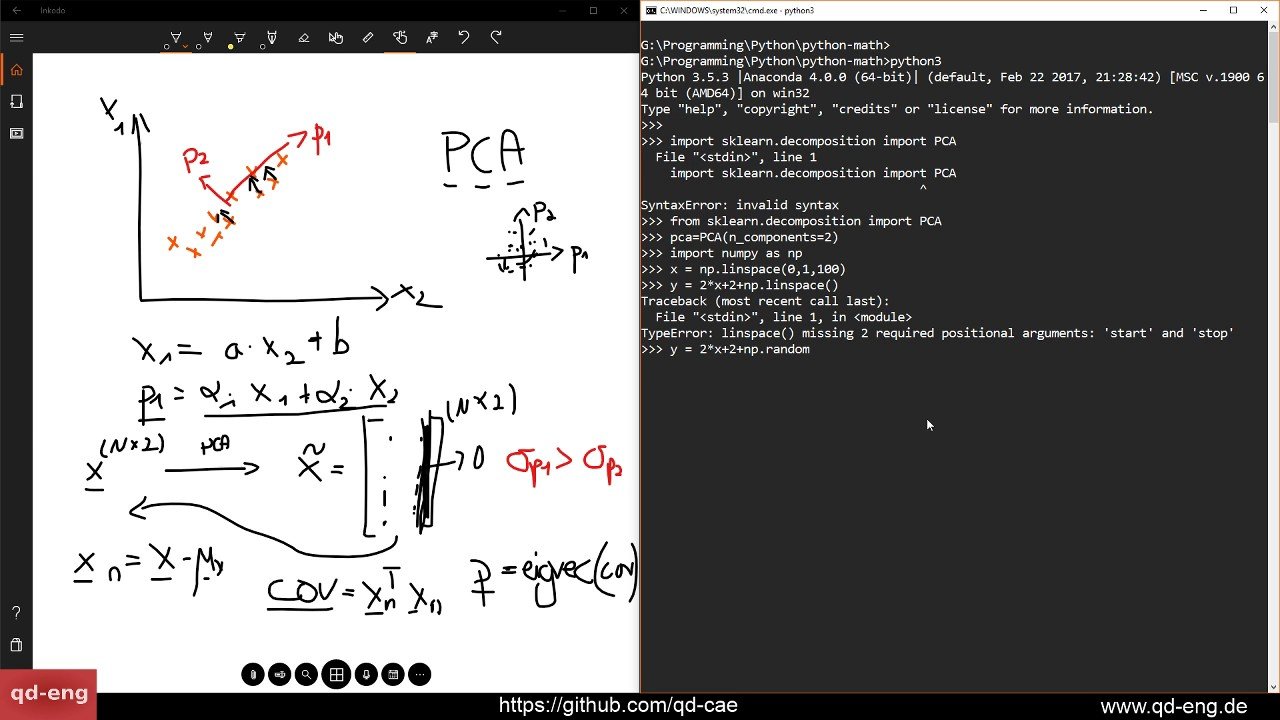
This is a dimensionality reduction problem, perfect for Principal Component Analysis. We want to analyze the data and come up with the principal components a combined feature of the two.
We can do this by drawing a vector through these data points and projecting each point onto the line we create. We are transferring our data in two dimensions to only needing one dimension.
The Principles Of Mathematics
| Title page of first edition |
| 1903, 1938, 1951, 1996, and 2009 |
| Media;type |
|---|
The Principles of Mathematics is a 1903 book by Bertrand Russell, in which the author presented his famous paradox and argued his thesis that mathematics and logic are identical.
The book presents a view of the foundations of mathematics and Meinongianism and has become a classic reference. It reported on developments by Giuseppe Peano, , Richard Dedekind, Georg Cantor, and others.
In 1905 Louis Couturat published a partial French translation that expanded the book’s readership. In 1937 Russell prepared a new introduction saying, “Such interest as the book now possesses is historical, and consists in the fact that it represents a certain stage in the development of its subject.” Further editions were printed in 1938, 1951, 1996, and 2009.
Using Two Different Strategies Rooted In Linear Algebra To Understand The Most Important Formula In Dimensionality Reduction
This article assumes the reader is comfortable with the contents covered in any introductory linear algebra course orthogonality, eigendecompositions, spectral theorem, Singular Value Decomposition
Confusion of the proper method to do Principal Component Analysis is almost inevitable. Different sources espouse different methods, and any learner quickly deduces that PCA isnt really a specific algorithm, but a series of steps that may vary, with the final result being the same: data that is simplified into a more concise set of features.
After talking about the basic goal of PCA, Ill explain the mathematics behind two commonly shown ways to calculate PCA. The first one involves creating a covariance matrix and doing some eigen-calculations on it.
The second involves the Singular Value Decomposition . Of course, if youre more comfortable with either one of these intuitions, you can go ahead and just understand it that way, but the big point of this article is to give an overview of how the two ways of seeing it are exactly equivalent.
Also Check: How To Find Biological Grandparents Uk
Is It Better To Pay The Principal Or Interest
When you pay extra payments directly on the principal, you are lowering the amount that you are paying interest on. It can help you pay off your debt much more quickly. However, just making extra payments with money that you get from bonuses or tax returns is better than just paying on the loan.
Constructing The Covariance Matrix

We can simply and directly construct the covariance matrix by doing a simple matrix operation on our input matrix X.
Keeping in mind the exact formula for calculating the covariance of two features :
Using this, we can come up with a much more streamlined matrix multiplication to calculate covariance. Notice that our formula for covariance sums over the products of the differences of each feature and its corresponding mean.
What we can do to automate the process of subtracting the mean from each feature. We can normalize our matrix by subtracting the mean of each feature from each training example.
This leaves us with a modified, normalized X, where the mean over all the columns is 0. In datasets with features that range in values we might also want to divide each column by the standard deviation of the column, but since both of our data is 110 we dont have to do that.
Now, to calculate our covariance matrix, we can simply multiply the transpose of our normalized matrix Xnorm.
All that were missing is to divide each covariance summation by the amount of examples N, and we can do that by dividing our 2 x 2 output by N. So, the total formula for any covariance matrix : is as follows:
It never ceases to amaze just how much matrix notation can help simplify otherwise convoluted formulas. Imagine having to write out the formula for a convolution matrix using summations!
You May Like: What Is Said To Be The Origin Of Chemistry
Calculating Interest And Principal Components For A Single Payment
At any point during amortization you can precisely calculate how much any single payment contributes toward principal and interest. Businesses must separate the principal and interest components for two reasons:
How Inflation Affects Principal
Inflation does not affect the nominal value of the principal of a loan, bond, or other financial instruments. However, inflation does erode the real value of the principal.
Suppose the U.S. government issues $10 million worth of 10-year U.S. Treasury bonds. Each treasury has a face value, or principal, of $10,000. If the average annual rate of inflation over the next 10 years is 4%, then the real value of those bonds at maturity is only $6,755,641.69. Yes, the principal balance remains $10,000, and thats the nominal sum bondholders receive. However, the value of that $10,000 has declined to, effectively, $6,755.64. In other words, the principal has only 67% of its original purchasing power.
Bondholders can still recoup their original costs if the value of the interest income the bond has generated is greater than the lost principal value. They can track the amount of return, or yield, theyre getting on a bond. Theres the bonds nominal yield, which is the interest paid divided by the principal of the bond, and its current yield, which equals the annual interest generated by the bond divided by its current market price.
You May Like: Eoc Fsa Warm Ups Algebra 1 Answers
Calculations For Different Loans
The calculation you use depends on the type of loan you have. Most home loans are standard fixed-rate loans. For example, standard 30-year or 15-year mortgages keep the same interest rate and monthly payment for their duration.
For these fixed loans, use the formula below to calculate the payment. Note that the carat indicates that youre raising a number to the power indicated after the carat.
Payment = P x x ^n] / ^n – 1
Calculating Interest When The Time Is Given In Days
Deb Russell;
Suppose you want to borrow $6,300 from March 15, 2004, until January 20, 2005, at a rate of 8 percent. The formula will still be I = Prt; however, you need to calculate the days.
To do so, do not count the day the money is borrowed or the day the money is returned. To determine the days: March = 16, April = 30, May = 31, June = 30, July = 31, August = 31, September = 30, October = 31, November = 30, December = 31, January = 19. Therefore, the time is 310/365. A total of 310 days out of 365. This is entered into the t for the formula.
Also Check: What Is An Example Of Movement In Geography
Examples Of Principal In A Sentence
New York Review of BooksThe Cigarette CenturyToo Late American Boyhood Bluesprincipalprincipalprincipalprincipalsprincipal STATprincipal Milwaukee Journal Sentinelprincipal Detroit Free Pressprincipal CNNprincipal Dallas Newsprincipal WSJprincipal ABC Newsprincipal BostonGlobe.comprincipal The Courier-JournalprincipalWashington Postprincipal San Diego Union-Tribuneprincipal PEOPLE.comprincipal Arkansas Onlineprincipal oregonliveprincipal alprincipal chicagotribune.com
These example sentences are selected automatically from various online news sources to reflect current usage of the word ‘principal.’ Views expressed in the examples do not represent the opinion of Merriam-Webster or its editors. Send us feedback.
What Are The Types Of Simple Interest
Simple interest is of two types ordinary simple interest and exact simple interest. In the ordinary simple interest, a year is considered of 360 days while calculating the interest while in exact simple interest a year is considered of 365 days. Both methods use the same formula to calculate simple interest.
Recommended Reading: Who Is Responsible For The 2000 Year Death Of Chemistry
What Are The Roles Of A Principal
The role of a principal is to provide strategic direction in the school system. Principals develop standardized curricula, assess teaching methods, monitor student achievement, encourage parent involvement, revise policies and procedures, administer the budget, hire and evaluate staff and oversee facilities.
What Types Of Loans Use Simple Interest
Most banks;these days apply compound interest on loans because;in;this way;banks get more money as interest from their customers, but this method is more complex and hard to explain to the customers.;On the other hand, calculations become easy when banks;apply simple interest methods. Simple interest is;much useful when a customer;wants;a loan for a short period of time, for example, 1 month, 2 months, or 6 months.
When someone goes for a short-term loan using simple interest, the interest applies on a daily or weekly basis instead of a yearly basis. Consider that you borrowed $10,000;on simple interest at a 10% interest rate per year, so this 10% a year rate divide into a rate per day which is equal to 10/365 = 0.027%. So you have to pay $2.73;a day extra on $10,000.
Recommended Reading: Geometry Segment Addition Postulate Worksheet
What Is Principal Ideal Generated By $p$
I’m studying abstract algebra, with Dummit’s book.
Our professor introduced a lemma, and I’m confused with some concept.
Here is the lemma: “Let $R$ be an integral domain, and let $p$ be in $R$. Then $p$ is prime if and only if $R_p$ is a nonzero prime ideal.”
The proof of this lemma says that $p$ is prime if and only if $ab$ is divisible by $p$ then $x$ or $y$ is also divisible by $p$, and it is same with $ab$ in $R_p$ implies that $a$ or $b$ is also in $R_p$, and it is same as $R_p$ is a prime ideal.
I don’t know why “$p$ is prime if and only if $ab$ is divisible by $p$ then $x$ or $y$ is also divisible by $p$, and it is same with $ab$ in $R_p$ implies $a$ or $b$ also in $R_p$.” What is the principal ideal generated by $p$? Its mean is every ideal of $R$ is generated by $p$, right? But how we can say that $ab$ in $R_p$ implies that $a$ or $b$ is also in $R_p$?
What Is The Math Definition Of Principal
The “principal” is the sum of money invested or borrowed, beforeinterest or other revenue is added, or the remainder of that sumafter payments have been made. In math, this applies tofinance.
Registered users can ask questions, leave comments, and earn points for submitting new answers.
Already have an account? Log in
Ask questions, submit answers, leave comments
Earn points for using the site
Already have an account? Log in
Read Also: What Does Scale Drawing Mean In Math
Understanding Principal: Responsible Parties
The term principal also refers to the party who has the power to transact on behalf of an organization or account and takes on the attendant risk. A principal can be an individual, a corporation, a partnership, a government agency, or a nonprofit organization. Principals may elect to appoint agents to operate on their behalf.
The transaction a principal is involved in could be anything from a corporate acquisition to a mortgage. The term is usually defined in the transactions legal documents. In those documents the principal is everyone who signed the agreement and thus has rights, duties, and obligations regarding the transaction.
When a person hires a financial advisor, they are considered a principal, while the advisor is the agent. The agent follows instructions given by the principal and may act on their behalf within specified parameters. While the advisor is often bound by fiduciary duty to act in the principals best interests, the principal retains the risk for any action or inaction on the part of the agent. If the agent makes a bad investment, it is still the principal who loses the money.
What Does Principal Value Mean In Trig
5/5Principal ValuesTrigonometricprincipal valueis the
A principal value of a function is the value selected at a point in the domain of a multiple-valued function, chosen so that the function has a single value at the point.
Beside above, what is the principal value of cos / 2? 2 Answers. The principal value of cos–1 is 5/6.
Similarly, it is asked, what is principal value in inverse trigonometric functions?
Principal Value of Inverse Trigonometric Functions. When there are two values, one is positive and the other is negative such that they are numerically equal, then the principal value of the inverse trigonometric function is the positive one. For instance, the principal value of cos1 is /6.
How do you find the principal solution in trigonometry?
Solution of a trigonometric equation:
37 Related Question Answers Found
Also Check: How To Find Ksp Chemistry
What Is The Principal
The principal is the amount due on any debt before interest, or the amount invested before returns. All loans start as principal, and for every designated period;that the principal remains unpaid in full the loan will accrue interest and other fees. The same is true for investments, but instead of owing more on top of the principal the investor is earning more.
Principle Vs Principal: Usage Guide
Adjective
Evidence of confusion between principle and principal can be found even in publications overseen by professional editors. To keep these words straight, remember that principle functions only as a noun, and in its most common uses refers to a basic rule or law, as in a guiding principle or a matter of principle. If you are looking for an adjective form of this word, you must use principled, as in taking a principled stand. Principal functions as both a noun and an adjective. The noun has various meanings referring to someone with controlling authority the school principal or in a leading position the ballet’s two principals , but also has meanings relating to finance, law, and architecture. As an adjective, principal typically means “most important,” as in the principal reason.
You May Like: What Is The Importance Of Biology In Our Daily Life
Simple Interest Vs Compound Interest
Simple interest and compound interest are two ways to calculate interest on a loan amount. It is believed that compound interest is more difficult to calculate than simple interest because of some basic differences in both. Let’s understand the difference between simple interest and compound interest through the table given below:
| Simple Interest | |
| Simple interest is calculated on the original principal amount every time. | Compound interest is calculated on the accumulated sum of principal and interest. |
| It is calculated using the following formula: S.I.= P × R × T | It is calculated using the following formula: C.I.= P × t;-;P |
| It is equal for every year on a certain principal. | It is different for every span of the time period as it is calculated on the amount and not principal. |
Simple Interest: Tips and Tricks
- To find the time period, the day on which money is borrowed is not taken into account, but the day on which money has to be returned is counted.
- The rate of interest is the interest on every $100 for a fixed time period.
- Interest is always more in the case of compound interest as compared to simple interest.
- The formula or methods to calculate compound interest is derived from simple interest calculation methods.
- Rate of interest is always kept in fractions in the formula.
Think Tank:
To Find Principal When Time Interest And Rate Are Given
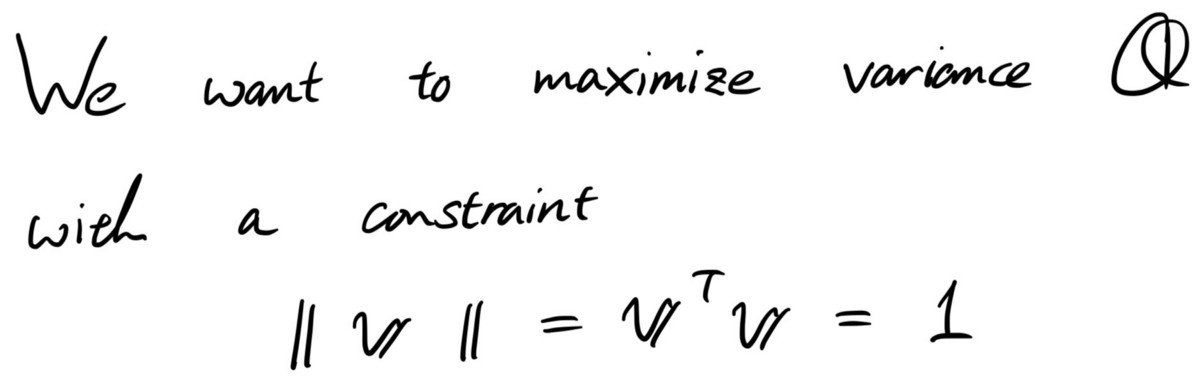
To find Principal when Time Interest and Rate are given the rules are.
Interest = /100
1.;Find Principal when Time = 3 years, Interest = $ 600; Rate = 4% p.a.Solution:
2. Find Principal when Time = 5 years, Interest = $ 500; Rate = 5% p.a.
Solution:
3. Find Principal when Time = 4 years, Interest = $ 400; Rate = 5% p.a.Solution:
Read Also: Is Ap Physics C Hard