Add A Free Hypotenuse Calculator Widget To Your Site
You can get a free online hypotenuse calculator for your website and you don’t even have to download the hypotenuse calculator – you can just copy and paste! The hypotenuse calculator exactly as you see it above is 100% free for you to use. If you want to customize the colors, size, and more to better fit your site, then pricing starts at just $29.99 for a one time purchase. Click the “Customize” button above to learn more!
What Is A Hypotenuse
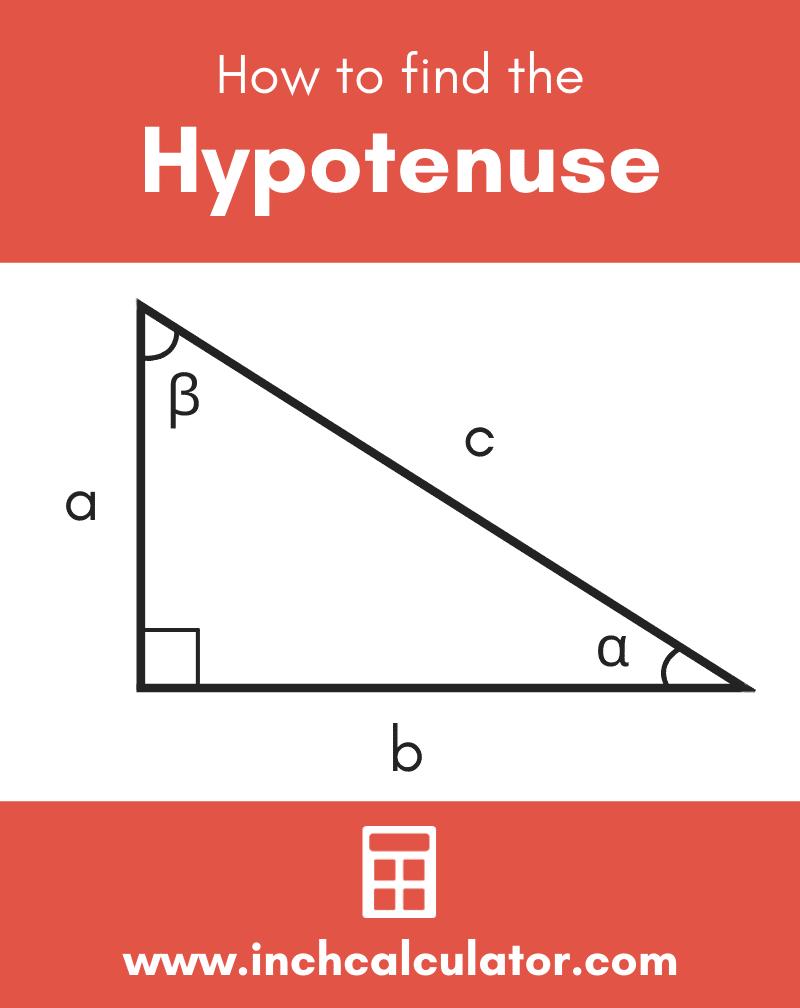
The hypotenuse is the longest side of a right-angled triangle. It is represented by the side opposite to the right angle. It is related to the other sides of the right triangle by the Pythagoras theorem. The square of the measure of the hypotenuse is equal to the sum of the squares of the other two sides of the right triangle. The hypotenuse can be easily recognized in a right triangle as the largest side.
Hypotenuse Definition: In a right-angled triangle, the longest side or the side opposite to the right angle is termed hypotenuse. The hypotenuse is related to the base and the altitude of the triangle, by the formula: Hypotenuse2 = Base2 + Altitude2. Let us look at the below real-world examples of a hypotenuse in right triangle-shaped objects.
How To Find Hypotenuse With Angle And Side
If an angle and a side are known, then we can calculate hypotenuse by applying the formula of trigonometric ratios. If A is the angle known, then we have,
- sin A = Perpendicular/Hypotenuse
- cos A = Base/Hypotenuse
So, if the length of the base is given, then the cos formula can be used and if height is known then the sin formula can be used to find the hypotenuse length.
You May Like: How Is Geography Related To History
The Hypotenuse Of A Triangle Formula
When you use a hypotenuse calculator, the detailing will surprise you. It incorporates several formulas to fit different circumstances you encounter. Scenario one: two right triangle legsWhen you have two right triangle legs, you can use the Pythagorean theorem to get your answer. To do so, you take the square root of the sum of squares. c = Where c = the longest side Scenario two: You have one angle and one legYou use the law of sines. c = a / sin = b / sinWhere c = the longest side a = the shortest sideScenario three: You have one leg and the areaYou will know that a right triangles area is equal to a x b / 2, so you would use the following formula: c = = ²) = ² + b²)
Finding The Hypotenuse Using The Law Of Sines
You May Like: Beginning And Intermediate Algebra 3rd Edition James W Hall
What Is A Right Triangle
A right triangle has the required three sides and three interior angles. One of its interior angles is a right angle, opposite the hypotenuse, with the other two sides — legs — meeting to form that right angle. In a right triangle a leg can also be called a cathetus .
The two legs are, by definition, two altitudes or heights of the right triangle the third altitude can be constructed by striking a perpendicular line segment from the hypotenuse to the right angle.
Using The Pythagorean Theorem
Don’t Miss: When Was Quantum Physics Discovered
Right Triangle Questions Using The Theorem
The Theorem helps us in:
There is a proof of this theorem by a US president. Its simplicity makes it is easy enough for the grade 8 kids to understand.
Finding The Hypotenuse Of Special Right Triangles
Also Check: What Is Ph In Biology
Examples Of Hypotenuse In A Sentence
hypotenuse Popular Mechanicshypotenuse Harpers Magazine hypotenuse Harpers Magazine hypotenuse Harpers Magazine hypotenuse Harpers Magazine hypotenuse Harpers Magazine hypotenuse Harpers Magazine hypotenuse Quanta Magazine
These example sentences are selected automatically from various online news sources to reflect current usage of the word ‘hypotenuse.’ Views expressed in the examples do not represent the opinion of Merriam-Webster or its editors. Send us feedback.
How Do You Find The Longest Side Of A Triangle
The hypotenuse is termed as the longest side of a right-angled triangle. To find the longest side we use the hypotenuse theorem, 2 = 2 + 2. For example, a bread slice is given in the shape of a right-angled triangle. If the base is 4 inches and the height is 3 inches, then the hypotenuse is 2 = 2 + 2 = = 25 = 5 inches.
Read Also: What Is The Meaning Of Geography
A Right Triangle’s Hypotenuse
The hypotenuse is the largest side in a right triangle and is always opposite the right angle.
. The other two sides of the triangle, AC and CB are referred to as the ‘legs’.
In the triangle above, the hypotenuse is the side AB which is opposite the right angle, $$ \angle C $$.
Online tool calculates the hypotenuse using the Pythagorean theorem.
How To Find Hypotenuse
To find the length of the hypotenuse of a triangle, we will be using the above equation. For that, we should know the values of the base and perpendicular of the triangle. For example, in a right triangle, if the length of the base is 3 units, and the length of the perpendicular side is 4 units, then the length of the hypotenuse can be found by using the formula Hypotenuse2 = Base2 + Perpendicular2. By substituting the values of the base and perpendicular, we get, Hypotenuse2 = 32 + 42 = 9 + 16 = 25. This implies that the length of the hypotenuse is 5 units. This is how we can easily find the length of the hypotenuse by using the hypotenuse equation.
Follow the steps given below to find the hypotenuse length in a right-angled triangle:
- Step 1: Identify the values of base and perpendicular sides.
- Step 2: Substitute the values of base and perpendicular in the formula: Hypotenuse2 = Base2 + Perpendicular2.
- Step 3: Solve the equation and get the answer.
Let us consider one more example to find the hypotenuse of a triangle. The longest side of the triangle is the hypotenuse and the other two sides of the right triangle are the perpendicular side with a measure of 8 inches, and the base with a measure of 6 inches.
Read Also: What Is Cell Structure In Biology
How Do You Find The Altitude Of A Hypotenuse
How To Find The Altitude On A Hypotenuse
In Maths, the altitude of a triangle means the line segment that connects the vertex and the side opposite to the vertex. The length of the altitude is simply called the altitude. Similarly, the altitude to the hypotenuse is the line segment that connects the hypotenuse of a right triangle and the vertex opposite to the hypotenuse through the perpendicular. In elementary geometry, the relationship between the length of the altitude on the hypotenuse of a right triangle and the line segment created on the hypotenuse is explained using the theorem called the Geometric Mean Theorem or Right Triangle Altitude Theorem. The altitude to the hypotenuse can be found as follows:
Step 1: In a right triangle, draw the altitude of the hypotenuse. The altitude creates the two new right triangles which are similar to each other and the main right triangle.
Step 2: Now, divide the length of the shortest of the main right triangle by the hypotenuse of the main right triangle.
Step 3: Now, multiply the result obtained from step 2 by the remaining side of the main right triangle.
Step 4: The result obtained is called the altitude or the height of the right triangle.
For example, if the sides of a right triangle a, b, and c are 3 cm, 4 cm, and 5 cm respectively, then the altitude on the hypotenuse is calculated as follows:
Here
a = perpendicular side = 3 cm
b= base side = 4 cm
C = hypotenuse = 5 cm
Here, the smallest side of the right triangle is equal to 3 cm.
Altitude = = 0.6
You May Like: Algebra 2 An Incremental Development
Using A Hypotenuse Calculator: Finding The Hypotenuse Of A Right Triangle
Formulas for a hypotenuse equation can be quite confusing unless you use a real-life example. Lets say you see a nest of baby birds in a 10-foot tree that doesnt have a mother to feed them. You want to retrieve the birds and look after them. You need to establish how long your ladder should be from the ground to the baby birds.1.Choose the scenario that fits the best from the previous formulas. The safest angle for your ladder is 80 degrees, and the height is 10 feet. You can enter this information into the hypotenuse calculator.2.The ladder length, which appears as the hypotenuse , is 10.154 feet. 3.You can then find out the second angle, which is 1.763 feet. The second angle is 10 degrees.
Units
History And Etymology For Hypotenuse
earlier hypothenusa, hypothenuse, borrowed from Latin hypotnsa, borrowed from Greek hypoteínousa, noun derivative from feminine of hypoteínn, present participle of hypoteínein“to stretch under, put under, subtend,” from hypo-hypo- + teínein“to stretch, extend” more at tenant entry 1
Note: The nominal use of hypoteínousa in Greek is apparent in passages such as the following, from the Deipnosophistae of Athenaeus of Naucratis , where “line/lines” or “side/sides” are understood: “Apollódros dè ho arithmtikòs kaì thûsaí phsin autòn hekatómbn epì tôi eurkenai hóti trignou orthogníou tn orthn gnían hypoteínousa íson dýnatai taîs periechoúsais .” the right angle is equal to the lines embracing it.)”
Recommended Reading: How To Find Uncertainty In Physics
What Is Hypotenuse Square
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides.
Finding The Missing Sides Of A Right Triangle
The theorem gives a relation among the three sides of a right-angled triangle. We can find one side if we know the other two sides. How?
Example: We are given below the two sides of the right triangle. Find the third side.
Given: a = 3, c = 5
Which side is the hypotenuse?
AC = c = 5
Always identify the hypotenuse first
Unknown side = BC = b?
Putting the values in the Pythagoras Formula: a2 + b2 = c2
32 + b2 = 52
b2 = 25 9 = 16 = 42
b = 4
You May Like: Mcdougal Littell Geometry 9.5 Answers
Examples On Hypotenuse Formula
Let us solve some interesting problems using the hypotenuse formula.
Example 1: Using hypotenuse formula solve for the longest side of the given bread slice that is similar to a right-angle triangle. Its height is 13 units and its base is 5 units.
Solution:
To find: The longest side of the bread slice.
Its height = 13 units.
hypotenuse formula = 2 +
==13.98
Answer: The longest side of the bread slice = 13.928 units.
Example 2: The hypotenuse of a right triangle is 5 units. Its base is 3 units. Find its height using the hypotenuse formula.
Solution:
To find: The height of the right triangle.Let us assume it to be ‘h’Its hypotenuse = 5 units.By using the hypotenuse formula,hypotenuse2 = 2 + 2
4 = h
Answer: The height of the right triangle = 4 units.
Example 3: Using the hypotenuse formula, solve for the longest side of the given bread slice that is similar to a right-angle triangle. Its height is 14 units and its base is 8 units.
Solution:
To find: The longest side of the bread slice.
Its height = 14 units.
hypotenuse formula = 2 +
Answer: The longest side of the bread slice = 16.124 units.
Sides Of A Right Triangle
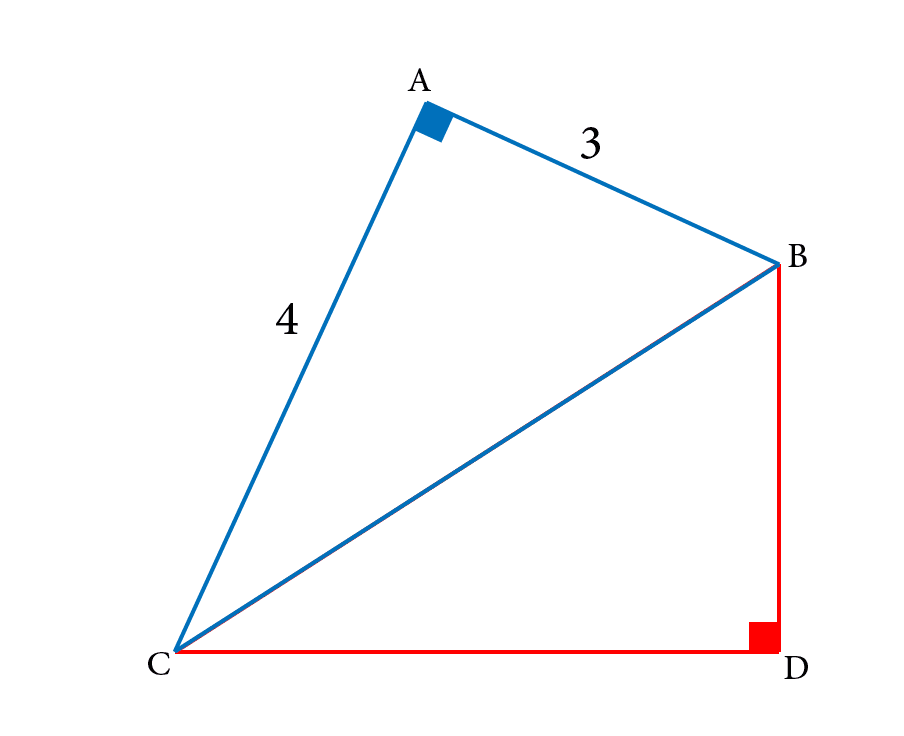
Hypotenuse, Adjacent and Opposite Sides.
In the following right triangle PQR,
- the side PQ, which is opposite to the right angle PRQ is called the hypotenuse.The hypotenuse is the longest side of the right triangle.
- the side RQ is called the adjacent side of angle .
- the side PR is called the opposite side of angle .
Note: The adjacent and the opposite sides depend on the angle .For complementary angle of , the labels of the 2 sides are reversed.
Example:Identify the hypotenuse, adjacent side and opposite side in thefollowing triangle: a) for angle xb) for angle y
Solution:a) For angle x: AB is the hypotenuse, AC is the adjacent side , and BC is the opposite side. b) For angle y: AB is the hypotenuse, BC is the adjacent side , and AC is the opposite side.
Read Also: What Are The Limitations And Legal Ramifications Of Psychological Restraint