How To Find Uncertainty In Physics

Increasing Precision With Multiple Measurements

One way to increase your confidence in experimental data is to repeat the same measurement many times. For example, one way to estimate the amount of time it takes something to happen is to simply time it once with a stopwatch. You can decrease the uncertainty in this estimate by making this same measurement multiple times and taking the average. The more measurements you take , the better your estimate will be.

Taking multiple measurements also allows you to better estimate the uncertainty in your measurements by checking how reproducible the measurements are. How precise your estimate of the time is depends on the spread of the measurements and the number of repeated measurements you take.

Consider the following example: Maria timed how long it takes for a steel ball to fall from top of a table to the floor using the same stopwatch. She got the following data:

0.32 s, 0.54 s, 0.44 s, 0.29 s, 0.48 s

How Is Uncertainty Reported

When doing measurements, uncertainty needs to be reported.It helps those reading the results to know the potential variation.To do this, the uncertainty range is added after the symbol ±.

Lets say we measure a resistance value of 4.5ohms with an uncertainty of 0.1ohms.The reported value with its uncertainty is 4.5 ± 0.1 ohms.

We find uncertainty values in many processes, from fabrication to design and architecture to mechanics and medicine.

What Is Uncertainty And How Is It Measured

In metrology, measurement uncertainty is the expression of the statistical dispersion of the values attributed to a measured quantity. … Thus, the relative measurement uncertainty is the measurement uncertainty divided by the absolute value of the measured value, when the measured value is not zero.

Also Check: Algebra Nation Independent Practice Answer Key

Example: Calculate The Standard Deviation With The Equation Above

The following measurements are given:

5.4 6.7 3.8 5.1 6.3

Step 1: Calculate the mean of all the measurements.

The number of measurements is N=5, so the mean is:

/ 5 = 5.46

Step 2: Calculate the square of each sample minus the mean.

^2 = 0.0036

Step 3: Sum all those squares for all measurements.

0.0036 + 1.5376 + 2.7556 + 0.1296 + 0.7056 = 5.132

Step 4: Divide the sum by N and take the square root.

Sqrt = 1.0131

We want to have the same number of decimal points as for the mean, so we round it to 2 decimal places: 1.01

Step 5: State the final measurement.

The final measurement is the mean +/- the standard deviation, so our answer is 5.46 +/- 1.01.

Here you can use an online tool to calculate the standard deviation.

What Is Uncertainty In Physics

Even though science is known to able to make pretty accurate predictions, they are never exact. We use mathematical models to describe the world around us, but once we go ahead and make measurements of those predictions, we find that we cannot measure everything with a 100% accuracy. This is what we call uncertainty.

If we measure the length of an object with a ruler, the length that we read could be around 203 mm. But given that rulers are not perfect, and also that we might not be reading the measurement accurately enough, the actual length might actually be just a bit larger or smaller. Since the smallest distance we can measure with a ruler is 1 mm, our uncertainty is +/- 1 mm, and we can write our measurement as 203 mm +/- 1 mm. This means that the length is 203 mm, but it could vary up to 1 mm.

In the following sections we will see the process of calculating uncertainty.

Read Also: How Was Ancient Greek Civilization And Culture Affected By Geography

How To Convert Uncertainty To Standard Deviations

To convert uncertainty components to standard deviations, follow the steps listed below:

Refer to the chart below to find the divisor associated with the probability distribution that you selected in step 4.

Next, divide your uncertainty components by the appropriate divisor to convert them to a standard uncertainty. Afterward, all of your contributors should be on the same confidence level and equivalent to a standard deviation.

Also Check: What Type Of Math Is On The Ged

What About Indirect Measurements

If you are performing indirect measurements that require you to calculate your measurement results, then you should evaluate the equation used to determine your measurement result. Each variable in the equation will have its own uncertainty that will directly affect the uncertainty associated with the calculated measurement result.

To help you out, think of using dead weight testers or calibrating torque transducers and standard resistors. Each one of these measurement processes require you to use an equation to calculate a result for comparison purposes. To estimate uncertainty, you will want to break down the equation and evaluate the uncertainty of each variable in the equation.

If you want to learn more about specifying the measurement function and process for your uncertainty analysis, check out this guide:

Don’t Miss: Jonathan Thomas Child Of Rage Today

What Does Uncertainty Mean In Science

Scientific uncertaintyuncertaintyscienceuncertaintyTo help organizations accomplish this goal, I have compiled a list of three highly-effective methods to reduce measurement uncertainty.

What Do You Mean By Uncertainty

Uncertainty as used here means the range of possible values within which the true value of the measurement lies. This definition changes the usage of some other commonly used terms. For example, the term accuracy is often used to mean the difference between a measured result and the actual or true value.

Recommended Reading: My Hrw Answers

What Is Instrumental Uncertainty

4/5Instrumental Uncertaintiesuncertainty

Likewise, people ask, how do you find instrumental uncertainty?

Instrumental Uncertainty = 0.05 grams. Record measurements to the hundredths place with the digit either a 5 , or a 0 . Examples: 27.05 g, 32.30 g.

Also, what is the uncertainty of a meter stick? Therefore the instrument uncertainty for the meter stick is ±0.1 cm. . Sometimes, one can estimate the instrument uncertainty by interpolation. The interpolation is usually estimated as a multiple of ½, 1/3 or 1/5, etc of the smallest division on the instrument.

Regarding this, what is an example of uncertainty?

noun. Uncertainty is defined as doubt. When you feel as if you are not sure if you want to take a new job or not, this is an example of uncertainty. When the economy is going bad and causing everyone to worry about what will happen next, this is an example of an uncertainty.

What is uncertainty in statistics?

Uncertainty in statistics is measured by the amount of error in an estimate of the mean or average value of a population.

How To Calculate Uncertainty

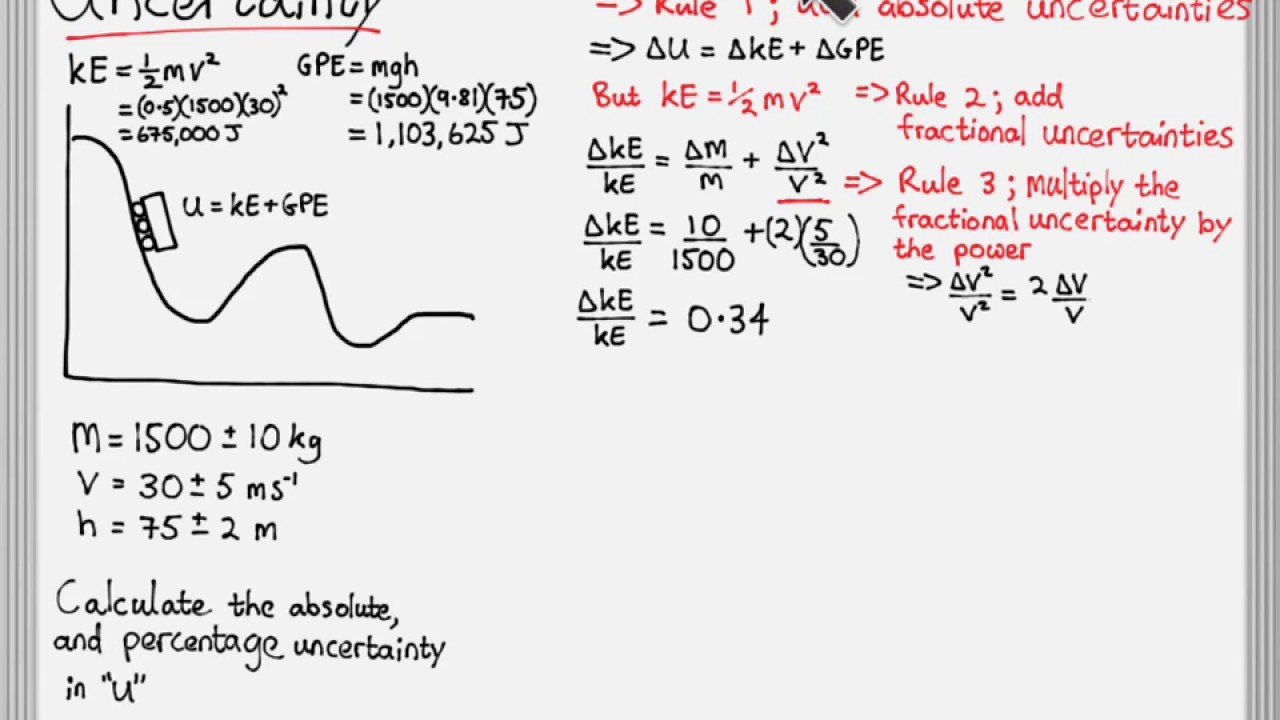
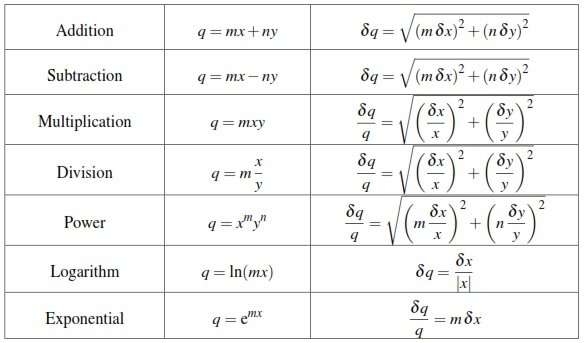
Quantifying the level of uncertainty in your measurements is a crucial part of science. No measurement can be perfect, and understanding the limitations on the precision in your measurements helps to ensure that you dont draw unwarranted conclusions on the basis of them. The basics of determining uncertainty are quite simple, but combining two uncertain numbers gets more complicated. The good news is that there are many simple rules you can follow to adjust your uncertainties regardless of what calculations you do with the original numbers.

TL DR

If youre adding or subtracting quantities with uncertainties, you add the absolute uncertainties. If youre multiplying or dividing, you add the relative uncertainties. If youre multiplying by a constant factor, you multiply absolute uncertainties by the same factor, or do nothing to relative uncertainties. If youre taking the power of a number with an uncertainty, you multiply the relative uncertainty by the number in the power.

You May Like: Angle Addition Worksheets

Root Sum Of Squares Method

If you are a more visual learner, like me, take a look at the process below to see if it makes more sense.

Below, you will see the equation for calculating the combined uncertainty.

This is the equation that I typically use since I usually include sensitivity coefficients earlier in the process before I convert uncertainty components to standard deviations.

If you evaluate measurement uncertainty the same way, you should be able to use the simplified equation. If you do not use sensitivity coefficients at all, you can use the simplified equation as well.

Both equations give you the same result. So, use the equation that works best for you. If you are using an excel spreadsheet calculator, you may find the function in the next section beneficial.

Measurement Functions Without Equations

Most of the measurement functions that you evaluate will not have equations. So, you will need to evaluate the measurement process to find the factors that influence measurement uncertainty.

Start by evaluating the core elements of the measurement process, including the:

Using the items in the list above, you should be able determine how much uncertainty is contributed from each source. If you need help, you can contact me for additional guidance or hire me to analyze the data for you.

Evaluate Information and Select the Right Data

Next, you need evaluate the information that you have and find data that you will use for estimating uncertainty. You need to find data related to your uncertainty analysis and eliminate everything else from consideration.

This should include information and data related to your:

Analyze the Data

Then, analyze the data that you have using appropriate methods of analysis to find the magnitude of each uncertainty component. You can analyze data in many ways, so choose methods that are appropriate for the data you are analyzing.

If you need help, get a quality statistics textbook or check the free NIST SEMATECH Engineering Statistics Handbook. You can also check out some of my guides on quantifying sources of uncertainty.

Quantify Uncertainty Components

You can add the uncertainty and unit of measurement directly into your uncertainty budget.

Read Also: Paris Jackson Biological Parents

Relevance And Uses Of Uncertainty Formula

From the perspective statistical experiments, the concept of uncertainty is very important because it helps a statistician to determine the variability in the readings and estimate the measurement with a certain level of confidence. However, the precision of the uncertainty is only as good as the readings taken by the measurer. Uncertainty helps in estimating the best approximation for a measurement.

Excel Function For Combining Uncertainty

If you use Microsoft Excel to estimate uncertainty, you can easily combine uncertainty using the formula below. It is a combination of the square root and sum of squares function.

=sqrt)

Take a look at the image below to see the function used in my Simple Uncertainty Calculator.

If you want to learn more about calculating the combined uncertainty, click the link to read the guide:

Note:

To meet ISO/IEC 17025:2017 requirements, you must expand uncertainty to approximately 95%. Most people use an expansion factor of 2 to achieve a confidence interval of 95.45%. However, you can also use an expansion factor of 1.96 for a confidence interval of exactly 95.00%.

Additionally, you can find your coverage factor using the Students T table. This is not common, but it is an option if you need it. Just calculate the effective degrees of freedom using the Welch Satterthwaite equation and use the table to find the right coverage factor to achieve a 95% confidence interval.

The choice is yours. Just make sure to select an expansion factor that you will consistently use in each of your uncertainty analyses. Furthermore, it helps to know why you chose your expansion factor so you can justify it to assessors .

TIP:

Read Also: Punchline Bridge To Algebra 2nd Edition Answer Key

Selected Solutions To Problems & Exercises

1. 57.9 m/s 9.55 × 109 eV From Table 1 in Photon Energies and the Electromagnetic Spectrum, we see that typical molecular binding energies range from about 1eV to 10 eV, therefore the result in part is approximately 9 orders of magnitude smaller than typical molecular binding energies.

3. 29 nm 290 times greater

• College Physics. : OpenStax College. Located at: . License: CC BY: Attribution. License Terms: Located at License

How Do You Calculate Uncertainty In Physics Gcse

4.7/5Estimating uncertainty from sets of repeat measurements

In respect to this, what is GCSE physics uncertainty?

AQA Science: Glossary – UncertaintyThe interval within which the true value can be expected to lie, with a given level of confidence or probability, e.g. “the temperature is 20°C ± 2°C, at a level of confidence of 95%.”

Additionally, what is the uncertainty in physics? In metereology, physics, and engineering, the uncertainty or margin of error of a measurement, when explicitly stated, is given by a range of values likely to enclose the true value.

Hereof, what is the percentage uncertainty?

It is computed as: The percent uncertainty can be interpreted as describing the uncertainty that would result if the measured value had been100 units . A similar quantity is the relative uncertainty .

Why is uncertainty important in physics?

Improving quality is the key to mitigating risks and reducing costs. However, measurement uncertainty is a parameter that is often overlooked. It is an important aspect of measurement that affects quality, costs, decisions, and risks. The need for increased accuracy is not as important as the need to measure quality.

Also Check: Geometry Dash Icon Hack

State Units In The Accepted Si Format

There are several ways to write most derived units. For example: meters per second can be written as m/s or m s-1. It is important to note that only the latter, m s-1, is accepted as a valid format. Therefor, you should always write meters per second as m s-1 and meters per second per second as m s-2. Note that this applies to all units, not just the two stated above.

Describe And Give Examples Of Random And Systematic Errors

Random errorsA random error, is an error which affects a reading at random.Sources of random errors include:

• The observer being less than perfect
• The readability of the equipment
• External effects on the observed item

Systematic errors

A systematic error, is an error which occurs at each reading.Sources of systematic errors include:

• The observer being less than perfect in the same way every time
• An instrument with a zero offset error
• An instrument that is improperly calibrated

Recommended Reading: How Do You Find The Displacement

Mixtures Of Multiplication Division Addition Subtraction And Powers

If z is a function which involves several terms added or subtracted we must apply the above rules carefully. This is best explained by means of an example.

Example: w = cm, x = cm, y = cm. Find z = w x +y^2 z = wx +y^2 = 18.0
First we compute v = wx as in the example in to get v = . Finally, we compute Dz = Dv + D = 0.9 + 3.6 = 4.5 rounding to 4	We have v = wx = cm. The calculation of the uncertainty in is the same as that shown to the left. Then from Eq. 1b Dz = 3.7

Plotting Uncertainties And Errors

Uncertainties are plotted as bars in graphs and charts.The bars extend from the measured value to the maximum and minimum possible value.The range between the maximum and the minimum value is the uncertainty range. See the followingexample of uncertainty bars:

Figure 1. Plot showing the mean value points of each measurement. The bars extending from each point indicate how much the data can vary. Source: Manuel R. Camacho, StudySmarter.

See the following example using several measurements:

You carry out four measurements of the velocity of a ball moving 10 metres whose speed is decreasing as it advances.You mark 1-metre divisions, using a stopwatch to measure the time it takes for the ball to move between them.

You know that your reaction to the stopwatch is around 0.2m/s.Measuring the time with the stopwatch and dividing by the distance, you obtain values equal to 1.4m/s, 1.22m/s, 1.15m/s, and 1.01m/s.

Because the reaction to the stopwatch is delayed, producing an uncertainty of 0.2m/s, your results are 1.4 ± 0.2 m/s, 1.22 ± 0.2 m/s, 1.15 ± 0.2 m/s, and 1.01 ± 0.2m/s.

The plot of the results can be reported as follows:

Figure 2. The plot shows an approximate representation. The dots represent the actual values of 1.4m/s, 1.22m/s, 1.15m/s, and 1.01m/s. The bars represent the uncertainty of ±0.2m/s. Source: Manuel R. Camacho, StudySmarter.

Read Also: Are Michael Jackson’s Children His Biological Children

Perform Arithmetic Operations With Uncertain Measurements

Recommended Reading: Geometry Segment Addition Postulate Worksheet