What Is Measurement In Physics

What Is The International System Of Units

After learning the importance of units and measurements, let us focus on the International System of Units. Traditionally, people didnt have any measuring devices to calculate standard measurement units. To tackle this problem, they devised different innovative measuring methods with the available tools. For example, they used a foot as a measurement of length. 1 foot is around 0.3 metres which are 30 cm. Another measurement our ancestors used for length was a league. One league was the distance covered by a person when we walked for an hour. This unit, however, is no longer in use.

To tackle this problem of different systems of measurement , a system of units called the International System of Units was established and has been adopted by most developed and developing countries. Although this has been established and adopted across major fields like science and technology and government operations, people normally refer to their customary or traditional units. For example, in the United States of America, people even now refer to lengths in terms of inches and feet instead of centimetres and metres.

Standard Units Of Measurement

Standard Units of Measurements Units that have a fixed quantity and do not vary from person to person and place to place are called standard units. For example, the metric system, created by the French in 1790, is a standard set of units.

Adopting standard units of measurement does not solve the problem. People in different countries may be using a different set of standard measurement units. For the sake of uniformity, scientists all over the world have adopted a common set of units. This system is called the International System of Units or the SI units. The adoption of SI units in 1960 made it easier for scientists of different countries to communicate their results to one another.

The SI unit of length is metre. Some common standard units of length are inch, millimetre, centimetre, and kilometre.

Depending on the size of the object, we need to measure, we have to choose an appropriate unit. For example, we use metres to measure the length of a piece of cloth, kilometres to measure the distance from one place to another, millimetres to measure the thickness of the hair, and so on. Centimetre and millimetre are used to measure shorter distances while kilometre is used to measure longer distances.

Example 1: Raju and his friend Akhil live 2000 m from each other. Express the distance between their houses in kilometres .Solution: We know that 1000 m = 1 km Therefore, 2000 m = 2 km Therefore, the distance between the two houses is 2 km.

What Is Measurement In Physics

Measurement is the process of finding the length, size, or quantity of a substance. Since ancient times, people have used several ways to measure length. A physical quantity has to be measured with respect to some fixed quantity. A fixed quantity with respect to which a physical quantity is measured is called a unit. A unit is used as a standard of measurement. In early times, people used different body parts like hand span, cubit, and fathom to measure length.

Foot, pace, and yard are some other units of length based on body parts. However, these units are not reliable as the length of body parts varies from person to person. Therefore, people realized the need for

Don’t Miss: What Is Uneven Development In Geography

Unit Of Measurement In Physics

As mentioned earlier, units of measurement provide a reference standard to identify the measurement of a physical quantity.

They provide specific meaning to the magnitude of a substance. For example, if we say that the volume of the book is 32, we wont have actual meaning about it. Its because the volume could be 32 mm3 or 32 cm3 or 32 m3.

However, if we use units like cm3, we get the actual meaning that the volume of the book is 32 cm3.

How To Prepare For Physics And Measurements

First, you should have a basic idea about various measurement units of different physical quantities like length, mass, time. Also, you should have an idea about SI units and practical units like liters, ton, etc. which we use in our daily life. Please try to remember the most used formulas and units of quantities by practicing the questions and watching video lectures on each concept. Practice enough problems of finding dimensions, units, error measurement so that it becomes easy to remember different formulas.

How to Solve Questions of Physics and Measurements:

• Denote a basic/fundamental quantity by a particular symbol. For example- Mass is denoted by M, length by L, time by T. To find the dimension of a physical quantity, express that quantity in terms of basic quantities as the product of different powers of the basic quantities and the result that we obtain after the product is the dimension. Lets understand this with the help of one example:

For example:-

as dimension of speed is

You can solve all these questions with proper study and once you start solving examples of these topics. Always do the calculations with proper concentration and neatly to avoid getting confused.

Recommended Reading: What Are The Branches Of Human Geography

Example: Calculate The Standard Deviation With The Equation Above

The following measurements are given:

5.4 6.7 3.8 5.1 6.3

Step 1: Calculate the mean of all the measurements.

The number of measurements is N=5, so the mean is:

/ 5 = 5.46

Step 2: Calculate the square of each sample minus the mean.

^2 = 0.0036

Step 3: Sum all those squares for all measurements.

0.0036 + 1.5376 + 2.7556 + 0.1296 + 0.7056 = 5.132

Step 4: Divide the sum by N and take the square root.

Sqrt = 1.0131

We want to have the same number of decimal points as for the mean, so we round it to 2 decimal places: 1.01

Step 5: State the final measurement.

The final measurement is the mean +/- the standard deviation, so our answer is 5.46 +/- 1.01.

Here you can use an online tool to calculate the standard deviation.

How Do You Reduce Uncertainty In Physics

Scientists are always trying to find ways to reduce the uncertainty in experiments, since a smaller uncertainty leads to more confident and more accurate results.

If you are taking experimental data, a way to reduce the uncertainty is to make several measurements and take the mean between them. Let us say for instance that you are studying a pendulum and want to calculate its period. Since you are the one stopping the clock, one can easily see that it is fairly difficult to measure the period precisely. Sometimes you might stop the clock a bit sooner or a bit later than you should. But if you take several measurements and take the mean, it is more likely that you will arrive to a more accurate estimate. Here we can also calculate the standard deviation. If it is very small, then you can conclude that you have taken very similar measurements. If on the other hand, the standard deviation is large, then the values are much spread apart.

Another source of uncertainty can be the device you are measuring with. If you use a very cheap ruler that seems to have inconsistencies, then the uncertainty will be higher than if you use a laser rangefinder. Also, if you are using a scale that is not correctly calibrated, you will get values that are not right. Therefore, you should be careful what you are measuring with, so that you know what level of confidence you have.

Also Check: How To Find Precision In Chemistry

Advantages Of Si Units

The SI units of measurement system have several distinct advantages over all other systems in use. The main advantages of SI units are as follows:

• SI units are simpler than all other system of units.
• The SI units system is comprehensive. i.e., the seven base units of the SI system cover all branches of science, engineering and technology.
• SI is a rational system of units. i.e., this system makes use of one unit for one physical quantity.
• SI unit system is coherent. i.e., All the derived units can be easily obtained from fundamental and supplementary units through their multiplication or division.
• The fundamental units of SI satisfy all the characteristics that a unit should have.
• SI unit system is a metric system. i.e., multiples and submultiples of the units can be easily expressed as powers of 10.
• SI units are internationally accepted.

Defining Error And Uncertainty

Some of the terms in this module are used by different authors in different ways. As a result, the use of some terms here might conflict with other published uses. The definitions used in this module are intended to match the usage in documents such as the NIST Reference on Constants, Units and Uncertainty.

For example, the term error, as used here, means the difference between a measured value and the true value for a measurement. Since the exact or “true” measured value of quantity can often not be determined, the error in a measurement can rarely be determined. Instead, it is more consistent with the NIST methods to quantify the uncertainty of a measurement.

Uncertainty as used here means the range of possible values within which the true value of the measurement lies. This definition changes the usage of some other commonly used terms. For example, the term accuracy is often used to mean the difference between a measured result and the actual or true value. Since the true value of a measurement is usually not known, the accuracy of a measurement is usually not known either. Because of these definitions, we modified how we report lab results. For example, when students report results of lab measurements, they do not calculate a percent error between their result and the actual value. Instead, they determine whether the accepted value falls within the range of uncertainty of their result.

You May Like: What Is Running Water In Geography

Measurement Definition In Science

• Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
• B.A., Physics and Mathematics, Hastings College

In science, a measurement is a collection of quantitative or numerical data that describes a property of an object or event. A measurement is made by comparing a quantity with a standard unit. Since this comparison cannot be perfect, measurements inherently include error, which is how much a measured value deviates from the true value. The study of measurement is called metrology.

There are many measurement systems that have been used throughout history and across the world, but progress has been made since the 18th century in setting an international standard. The modern International System of Units bases all types of physical measurements on seven base units.

Books For Physics And Measurement

For Physics and Measurements, you will find easy to moderate level questions in NCERT books, please solve them first. Then you can do questions from Understanding Physics by D.C. Pandey or H.C. Verma. Both of these books have good quality questions. But apart from these books, you should also give topic-wise online mock tests.

Also Check: What Are The Psychological Effects Of Incarceration

Why Is Uncertainty Important In Physics

Uncertainty is a very important concept in science in general. Scientists use experiments to validate or refuse a hypothesis, and therefore a good understanding of uncertainty is crucial if we get results that might debunk a theory.

Some people think uncertainty means a lack of knowledge. However, uncertainty is rather a measure of how well something is known. If a theory has a certain uncertainty, it does not mean it is wrong. It just tells us within what bounds the theory can be assumed to be correct. As more research is made, the uncertainty can be reduced. However, some people interpret the uncertainty of a theory as a synonym for doubt. If one understands what uncertainty actually means, one would come to the realization that stating the uncertainty is simply the scientists wanting to be as honest as possible as to how confident they are of their results.

Tips For Physics And Measurement

Because as said by Carl Sandburg:

“Time is the most valuable coin in your life. You and you alone will determine how that coin will be spent. Be careful that you do not let other people spend it for you.”

Also Check: What Is Sin In Geometry

Measurement Instruments And Systems

In general, measuring systems comprise a number of functional elements. One element is required to discriminate the object and sense its dimensions or frequency. This information is then transmitted throughout the system by physical signals. If the object is itself active, such as water flow, it may power the signal if passive, it must trigger the signal by interaction either with an energetic probe, such as a light source or X-ray tube, or with a carrier signal. Eventually the physical signal is compared with a reference signal of known quantity that has been subdivided or multiplied to suit the range of measurement required. The reference signal is derived from objects of known quantity by a process called calibration. The comparison may be an analog process in which signals in a continuous dimension are brought to equality. An alternative comparison process is quantization by counting, i.e., dividing the signal into parts of equal and known size and adding up the number of parts.

One important type of measurement is the analysis of resonance, or the frequency of variation within a physical system. This is determined by harmonic analysis, commonly exhibited in the sorting of signals by a radio receiver. Computation is another important measurement process, in which measurement signals are manipulated mathematically, typically by some form of analog or digital computer. Computers may also provide a control function in monitoring system performance.

Need For Standard Units And Measurement

There are many systems and units in place for measuring different quantities like length, area, mass, volume and other things. For example, an acre is a common way of representing area measurement in India. One acre is around 4046 square metres, according to the metric system. So now you can guess how difficult it would be if there were no standard units and measurements.

Similarly, the temperature is measured in degree celsius, and the same unit of measurement cannot be used to measure the length of a rod. Each quantity has to be measured in its own way. The magnitude and the measurement vary along with the quantity. Hence the need for the units of measurement for each quantity arises.

Read More:Unit conversion

Read Also: Does The Biological Father Have To Sign Adoption Papers

Absolute And Relative Uncertainty

It is first important to understand the distinction between the two. Absolute uncertainty is what we have seen so far, where the uncertainty is given in units of the original measurement, for example 5.6 mm +/- 0.3 mm.

But is 0.3 mm a lot of uncertainty? It surely depends what we are measuring. If we are measuring the distance to the sun, then 0.3 mm is a very small number. On the other hand, if we are measuring the width of a hair, then 0.3 mm becomes relevant. This is where relative uncertainty comes into play. It gives the uncertainty as a percentage of the original measurement.

For our example 5.6 mm +/- 0.3 mm, the relative uncertainty would be *100 = 5.4%

So, we can write 5.6 mm +/- 5.4%

Physics Chapter Wise Notes For Engineering And Medical Exams

This can be solved using:

The relationspeed of light Therefor dimension of a = dimension of =

• Another important section in this chapter is Errors In Measurement. This concept is used in the chapter Experimental Skills and in many problems from other chapters.

For Example- calculation of absolute error for a set of readings of the period of a simple pendulum etc.

Let’s see another example from Errors

Question- The percentage of errors in quantities P, Q, R, and S are 0.5%, 1%, 3%, and 1.5%

respectively in the measurement of a physical quantity

The maximum percentage error in the value of A will be :

This can be solved using the concept :

Error in quantity raised to some power — wherein

= absolute error in the measurement of a

= absolute error in the measurement of b

= absolute error in the measurement of x

Recommended Reading: How To Add Compounds Chemistry

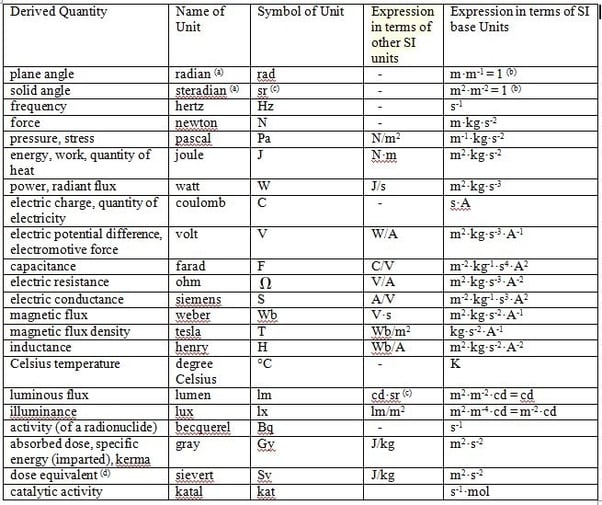
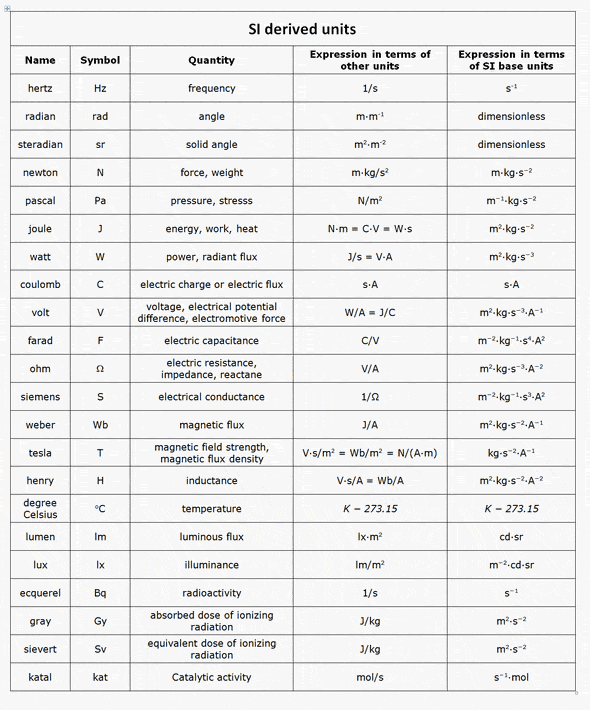
Si Units Of Measurement

The measurement system which is internationally accepted now is the one suggested by the Eleventh general conference of weights and Measures held in 1960 in France, and is known as Systeme Internationale d Unites or International System of Units abbreviated as SI units of measurement.According to this system, there are seven basic or fundamental units and three supplementary units. The basic units are

The supplementary units are

• the radian for angle,
• the steradian for solid angle,
• the becquerel for radioactivity.

Accuracy Precision And Significant Figures

Science is based on experimentation that requires good measurements. The validity of a measurement can be described in terms of its accuracy and its precision . Accuracy is how close a measurement is to the correct value for that measurement. For example, let us say that you are measuring the length of standard piece of printer paper. The packaging in which you purchased the paper states that it is 11 inches long, and suppose this stated value is correct. You measure the length of the paper three times and obtain the following measurements: 11.1 inches, 11.2 inches, and 10.9 inches. These measurements are quite accurate because they are very close to the correct value of 11.0 inches. In contrast, if you had obtained a measurement of 12 inches, your measurement would not be very accurate. This is why measuring instruments are calibrated based on a known measurement. If the instrument consistently returns the correct value of the known measurement, it is safe for use in finding unknown values.

The measurements in the paper example are both accurate and precise, but in some cases, measurements are accurate but not precise, or they are precise but not accurate. Let us consider a GPS system that is attempting to locate the position of a restaurant in a city. Think of the restaurant location as existing at the center of a bulls-eye target. Then think of each GPS attempt to locate the restaurant as a black dot on the bulls eye.

Uncertainty

Recommended Reading: What Is The Peter Principle In Psychology