Why Do I Need Trigonometry
This is a reasonable question, and the answer is at least partly because those who decide the mathematics curriculum in many countries think that you should know about it, and for very good reason.
Trigonometry is said to be the most important mathematical relationship ever discovered. Triangles are one of the most simple forms found in nature, but their mathematics has vital importance, especially where precise distance measurements are needed. When we begin to think about the applications where accurate distances are important, it is apparent that there are dozens, including navigation in naval and aviation systems, astronomy, satellite systems, geographical surveys and cartography , architecture and structural engineering, graphic design and computer generated imagery.
Many of these rely on a measurement technique known as triangulation, which applies the concepts of trigonometry.
Example: Trigonometry and Navigation
When you are sailing or cruising at sea, where you end up is affected by:
- The direction in which you steer
- The speed at which you travel in that direction and
- The direction and speed of the tide.
You can be motoring in one direction, but the tide could be coming from one side, and push you to the other. You will need trigonometry to work out how far you will travel and in what precise direction.
Worked Example
You have the opposite and the adjacent, which means that you need to use tangent. Tan = Opposite/adjacent = 5/10 = 0.5.
Ratios Through The Four Quadrants
You can deduce a few more ratios with the sum and difference formulas. You already did ratios for 75 degrees. Now, do those for 15 degrees. These formulas give ratios for angles at 15-degree intervals through the four quadrants. Plotting them out for the full 360 degrees, you can see how the three ratios change as the vector sweeps through the four quadrants.
Both the sine and cosine “wave” up and down between +1 and -1. Notice that the “waves” are displaced by 90 degrees, one from the other. This fact becomes important later.
The tangent starts out like the sine curve, but quickly it sweeps up to reach infinity at 90 degrees. Going “offscale” in the positive direction, it “comes on” from the negative direction on the other side of 90 degrees. Going through the 180-degree point, the tangent curve duplicates what it does going through 0 or 360 . At 270 degrees, it repeats what it did at 90 degrees.
Ratios Of Angles Greater Than 90 Degrees
So far, ratios of acute angles have been considered. Other triangles with obtuse angles might go over 180 degrees in later problems. To simplify classification of angles according to size, they are divided into quadrants.
A quadrant is a quarter of a circle. Since the circle is commonly divided into 360 degrees, the quadrants are named by 90-degree segments. 0-90 degrees is the 1st quadrant, 90-180 the 2nd, 180-270 the 3rd, and 270-360 the 4th.
Drawing in lines to represent the quadrant boundaries, with 0 or 360 horizontal to the right, 90 vertical up, 180 horizontal to the left, and 270 vertical down. Now, use this method for plotting graphs.
Progressively larger angles are defined by a rotating vector, starting from zero and rotating counterclockwise. Horizontal elements are x: positive to the right, negative to the left. Vertical elements are y. positive up, negative down. The rotating vector is r. So, the sine of an angle is y/r, the cosine x/r, and the tangent y/x. The vector r is always positive. So, the sign of the ratios can be figures for the various quadrants.
Also Check: Geometry Segment Addition Postulate Worksheet
Intuitive Understanding Of Sine Waves
Sine waves confused me. Yes, I can mumble “SOH CAH TOA” and draw lines within triangles. But what does it mean?
I was stuck thinking sine had to be extracted from other shapes. A quick analogy:
You: Geometry is about shapes, lines, and so on.
Alien: Oh? Can you show me a line?
You : Uh… see that brick, there? A line is one edge of that brick.
Alien: So lines are part of a shape?
You: Sort of. Yes, most shapes have lines in them. But a line is a basic concept on its own: a beam of light, a route on a map, or even–
Alien: Bricks have lines. Lines come from bricks. Bricks bricks bricks.
Most math classes are exactly this. “Circles have sine. Sine comes from circles. Circles circles circles.”
Argh! No – circles are one example of sine. In a sentence: Sine is a natural sway, the epitome of smoothness: it makes circles “circular” in the same way lines make squares “square”.
Let’s build our intuition by seeing sine as its own shape, and then understand how it fits into circles and the like. Onward!
Trigonometry Sine Cosine And Tangent
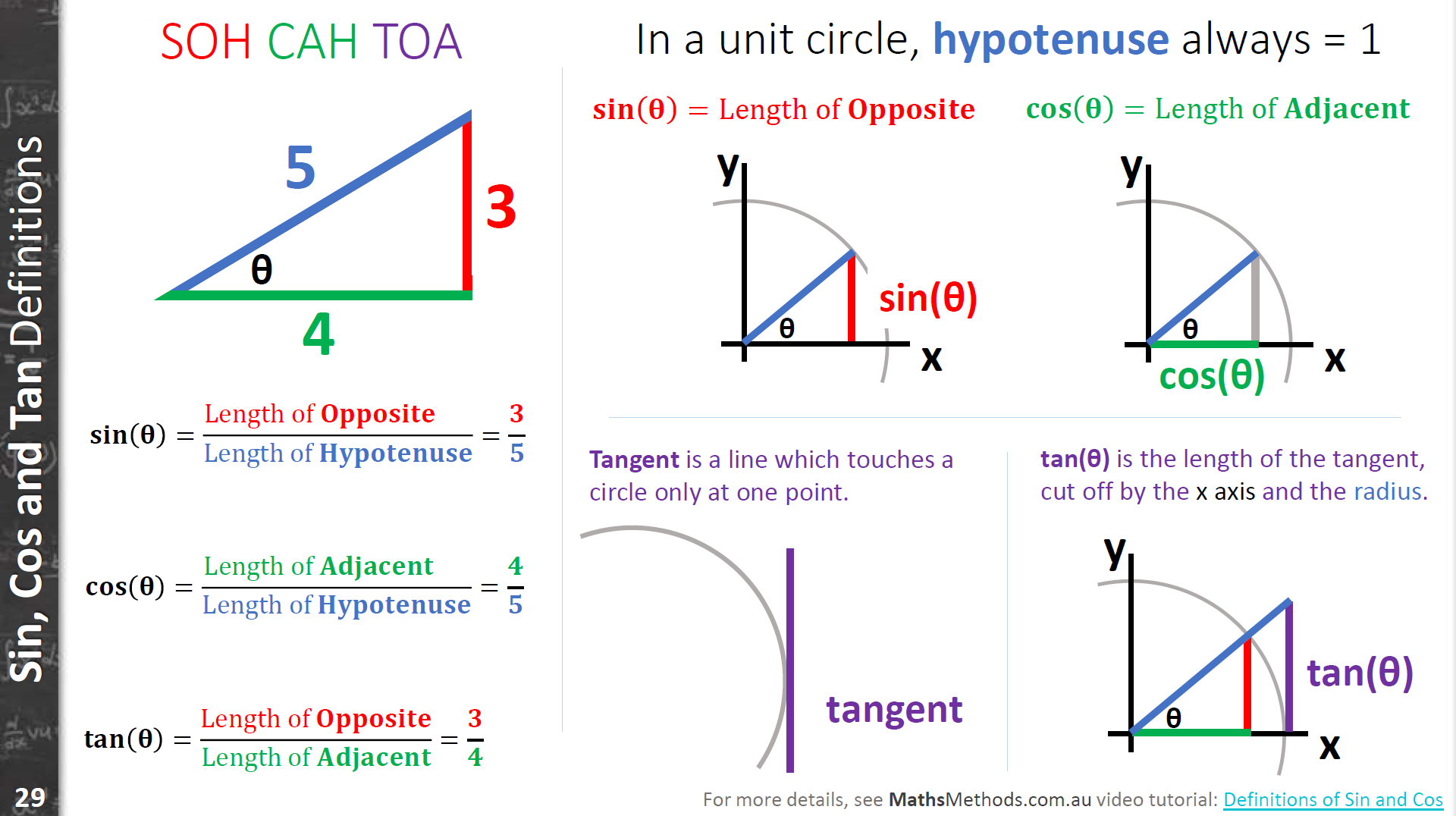
ABC is a right angled triangle
|
The angle A is 30 degrees. We write this as: |
a is the symbol for the side opposite angle A
b is the symbol for the side opposite angle B
c is the symbol for the side opposite angle C
Similar triangles are triangles in which all the angles in one triangle are equal to the angles in the other triangle
|
These two triangles are similar. The ratio between two sides in one triangle is equal to the ratio between the corresponding sides in the other triangle. |
Using the notation in the above triangles we get the following:
The ratio depends on the size of the angle.
Tangent
|
The ratio called tangent of an acute angle in a right angled triangle is defined as the ration between the side opposite the angle and the side adjacent to the angle . |
Don’t Miss: How To Do Elimination In Math
Trigonometry Calculator As A Tool For Solving Right Triangle
To find the missing sides or angles of the right triangle, all you need to do is enter the known variables into the trigonometry calculator. You need only two given values in the case of:
- one side and one angle
- two sides
- area and one side
Remember that if you know two angles, it’s not enough to find the sides of the triangle. Two triangles having the same shape may be of different sizes – that kind of relationship is called triangle similarity. If the sides have the same length, then the triangles are congruent.
Definition By Differential Equations
Sine and cosine can be defined as the unique solution to the initial value problem:
- d
- n . \sin x& =x-}}+}}-}}+\cdots \\& =\sum _^}}x^\\\cos x& =1-}}+}}-}}+\cdots \\& =\sum _^}}x^.\end}}
The radius of convergence of these series is infinite. Therefore, the sine and the cosine can be extended to entire functions , which are complex-valued functions that are defined and holomorphic on the whole complex plane.
Being defined as fractions of entire functions, the other trigonometric functions may be extended to meromorphic functions, that is functions that are holomorphic in the whole complex plane, except some isolated points called poles. Here, the poles are the numbers of the form (
- y \sin z& =\sin x\cosh y+i\cos x\sinh y\\\cos z& =\cos x\cosh y-i\sin x\sinh y\end}}
By taking advantage of domain coloring, it is possible to graph the trigonometric functions as complex-valued functions. Various features unique to the complex functions can be seen from the graph for example, the sine and cosine functions can be seen to be unbounded as the imaginary part of z becomes larger , and the fact that the functions contain simple zeros or poles is apparent from the fact that the hue cycles around each zero or pole exactly once. Comparing these graphs with those of the corresponding Hyperbolic functions highlights the relationships between the two.
Trigonometric functions in the complex plane
| sin |
Read Also: Geometry Dash Ericvanwilderman
Using Special Angles To Find Arcsin
While we can find the value of arcsine for any x value in the interval , there are certain angles that are used frequently in trigonometry whose sine and arcsine values may be worth memorizing. Below is a table showing these angles in both radians and degrees, and their respective sine values, sin.
| 90° |
| sin |
The values of sine from 0° through -90° follows the same pattern except that the values are negative instead of positive since sine is negative in quadrant IV. This pattern repeats periodically for the respective angle measurements, and we can identify the values of sin based on the position of in the unit circle, taking the sign of sine into consideration: sine is positive in quadrants I and II and negative in quadrants III and IV.
Once we’ve memorized the values, or if we have a reference of some sort, it becomes relatively simple to recognize and determine sine or arcsine values for the special angles.
Example:
arcsin is undefined because 3 is not within the interval -1arcsin1, the domain of arcsin.
Sum Of Angles In A Triangle
The theorem states that interior angles of a triangle add to 180°:
+ + = 180°
How do we know that? Look at the picture: the angles denoted with the same Greek letters are congruent because they are alternate interior angles. Sum of three angles , , is equal to 180°, as they form a straight line. But hey, these are three interior angles in a triangle! That’s why + + = 180°.
Read Also: Who Are Paris Jackson’s Parents
How To Find Sin Cos Tan Values
To remember the trigonometric values given in the above table, follow the below steps:
- First divide the numbers 0,1,2,3, and 4 by 4 and then take the positive roots of all those numbers.
- Hence, we get the values for sine ratios,i.e., 0, ½, 1/2, 3/2, and 1 for angles 0°, 30°, 45°, 60° and 90°
- Now, write the values of sine degrees in reverse order to get the values of cosine for the same angles.
- As we know, tan is the ratio of sin and cos, such as tan = sin /cos . Thus, we can get the values of tan ratio for the specific angles.
Sin Values
The Inverse Sine Function
For every trigonometry function such as sin, there is an inverse function that works in reverse. These inverse functions have the same name but with ‘arc’ in front.So the inverse of sin is arcsin etc. When we see “arcsin A”, we understand it as “the angle whose sin is A”
| sin30 = 0.5 | Means: The sine of 30 degrees is 0.5 |
| arcsin0.5 = 30 | Means: The angle whose sin is 0.5 is 30 degrees. |
You May Like: Algebra 2 An Incremental Development
Ratios For Sum Angles
As the examples showed, sometimes we need angles other than 0, 30, 45, 60, and 90 degrees. In this chapter you need to learn two things:1. Sin is not equal to sin A + sin B. It doesn’t work like removing the parentheses in algebra.2. The formula for what sin does equal.
First to show that removing parentheses doesn’t “work.” Here: make A 30 degrees and B 45 degrees.
Sin 30 is 0.5. Sin 45 is 0.7071. Adding the two is 1.2071.
You know that no sine can be more than 1. Why? the ratio has the hypotenuse as its denominator. The most that the numerator can be is equal to the denominator. A sine or cosine can never be greater than 1, so a value of 1.2071 must be wrong.
Ancient Egypt And The Mediterranean World
Several ancient civilizationsin particular, the Egyptian, Babylonian, Hindu, and Chinesepossessed a considerable knowledge of practical geometry, including some concepts that were a prelude to trigonometry. The Rhind papyrus, an Egyptian collection of 84 problems in arithmetic, algebra, and geometry dating from about 1800 bce, contains five problems dealing with the seked. A close analysis of the text, with its accompanying figures, reveals that this word means the slope of an inclineessential knowledge for huge construction projects such as the pyramids. For example, problem 56 asks: If a pyramid is 250 cubits high and the side of its base is 360 cubits long, what is its seked? The solution is given as 51/25 palms per cubit, and, since one cubit equals 7 palms, this fraction is equivalent to the pure ratio 18/25. This is actually the run-to-rise ratio of the pyramid in questionin effect, the cotangent of the angle between the base and face. It shows that the Egyptians had at least some knowledge of the numerical relations in a triangle, a kind of proto-trigonometry.
Read Also: Geometry Segment Addition Postulate Worksheet
Example 1 Find The Angle A
|
First Tan A = 3/4 = 0.75 |
We need to use the inverse function for tan, tan-1, to find the angle. This function is on the same key on the calculator as the tan function .
We use the following sequence of commands:
shift – tan-1 0.75 = 37º
Try the following on your calculator to see the difference between tan and tan-1:
angle ratio ratio angle
tan 37º = 0.75 tan-1 0.75 = 37º
Application Of Sin Cos Tan In Real Life
Trigonometry ratios sin, cos, tan find application in finding heights and distances in our daily lives. We use sin, cos, and tan to solve many real-life problems. Here is an example to understand the applications of sin, cos and tan.
Example: A ladder leans against a brick wall making an angle of 50o with the horizontal. If the ladder is at a distance of 10 ft from the wall, then up to what height of the wall the ladder reaches?
Solution:
Let us assume that the ladder reaches till x ft of the wall.
Using the given information:
Here, we know the adjacent side and we have to find the opposite side . So we use the relation between the opposite and the adjacent sides which is tan.
tan 50o = x/10
x = 10 tan 50o
x 11.9 ft
Here, tan 50o is calculated using the calculator and the final answer is rounded up to 1 decimal. Therefore, the ladder reaches up to 11.9 ft of the wall.
Topics Related to Sin Cos Tan:
Don’t Miss: What Is A Span Linear Algebra
Basic And Pythagorean Identities
Affiliate
Notice how a “co-” trig ratio is always the reciprocal of some “non-co” ratio. You can use this fact to help you keep straight that cosecant goes with sine and secant goes with cosine.
The following are called “Pythagorean” identities.
sin2 + cos2 = 1
1 + cot2 = csc2
Note that the three identities above all involve squaring and the number 1. You can see the Pythagorean-Thereom relationship clearly if you consider the unit circle, where the angle is t, the “opposite” side is sin = y, the “adjacent” side is cos = x, and the hypotenuse is 1.
We have additional identities related to the functional status of the trig ratios:
sin = sin
cos = cos
tan = tan
Notice in particular that sine and tangent are odd functions, being symmetric about the origin, while cosine is an even function, being symmetric about the y-axis. The fact that you can take the argument’s “minus” sign outside or eliminate it entirely can be helpful when working with complicated expressions.
Geeking Out With Calculus
Let’s describe sine with calculus. Like e, we can break sine into smaller effects:
- Start at 0 and grow at unit speed
- At every instant, get pulled back by negative acceleration
How should we think about this? See how each effect above changes our distance from center:
- Our initial kick increases distance linearly: y = x
- At any moment, we feel a restoring force of -x. We integrate twice to turn negative acceleration into distance:
Seeing how acceleration impacts distance is like seeing how a raise hits your bank account. The “raise” must change your income, and your income changes your bank account .
So, after “x” seconds we might guess that sine is “x” minus x^3/3! :
Something’s wrong — sine doesn’t nosedive! With e, we saw that “interest earns interest” and sine is similar. The “restoring force” changes our distance by -x^3/3!, which creates another restoring force to consider. Consider a spring: the pull that yanks you down goes too far, which shoots you downward and creates another pull to bring you up . Springs are crazy!
We need to consider every restoring force:
- y = x is our initial motion, which creates a restoring force of impact…
- y = -x^3/3!, which creates a restoring force of impact…
- y = x^5/5!, which creates a restoring force of impact…
- y = -x^7/7! which creates a restoring force of impact…
Just like e, sine can be described with an infinite series:
A few fun notes:
Recommended Reading: What Is The Molecular Geometry Of Ccl4
Values Of The Sine Function
There are many methods that can be used to determine the value for sine, such as referencing a table of cosines, using a calculator, and approximating using the Taylor Series of sine. In most practical cases, it is not necessary to compute a sine value by hand, and a table, calculator, or some other reference will be provided.
Angle Bisector Of A Triangle
Angle bisector theorem states that:
An angle bisector of a triangle angle divides the opposite side into two segments that are proportional to the other two triangle sides.
Or, in other words:
The ratio of the BD length to the DC length is equal to the ratio of the length of side AB to the length of side AC:
|BD|/|DC|= |AB|/|AC|
Read Also: Eoc Fsa Warm Ups Algebra 1 Answers