Corresponding Parts Of Congruent Triangles Are Congruent
In this video, you will learn how to use Corresponding Parts of Congruent Triangles are Congruent to prove line segments or angles are congruent to each other.
When writing proofs, we are not always directed to prove two triangles congruent but rather parts of the triangles congruent. With CPCTC, we can utilize congruence to prove parts of triangles congruent.
Lets look at an example:
Lets say that the two triangles are already congruent to each other. As a result, any corresponding parts of the triangles are congruent.
One of such might be ,
So if we proved that, we proved that these two triangles are congruent using Angle-Side-Angle.
The important thing is after we prove that we can show a lot of things.
We can list any corresponding parts of this triangle as being congruent.
Because we know corresponding parts of congruent triangles are congruent.
After this step, which is normally our last step, we can prove that
Our reason is simply that congruent parts of congruent triangles are congruent .
Then, we can use this to a lot of things.
We can also use this to prove that for the same reason which is CPCTC.
And we can also show that because congruent parts of congruent triangles are congruent .
Sometimes proving that two triangles are congruent isnt immediate stop in order to get to another proof about line segments or angles.
Possibly, even this information can be used to prove different triangles or maybe promises or squares or anything else are congruent.
Definition Of Congruence In Analytic Geometry
In a Euclidean system, congruence is fundamental it is the counterpart of equality for numbers. In analytic geometry, congruence may be defined intuitively thus: two mappings of figures onto one Cartesian coordinate system are congruent if and only if, for any two points in the first mapping, the Euclidean distance between them is equal to the Euclidean distance between the corresponding points in the second mapping.
A more formal definition states that two subsetsA and B of Euclidean spaceRn are called congruent if there exists an isometryf : Rn â Rn ) with f = B. Congruence is an equivalence relation.
How Do You Prove Cpctc Using Sss Criterion
In SSS triangle congruence all the three corresponding sides are equal. In other words, the two triangles are said to be congruent if all corresponding sides of one triangle are equal to the sides of another triangle. Thus, when two triangles are congruent then according to CPCTC all the corresponding angles are also equal.
Recommended Reading: Why Do We Drink Alcohol Psychology
Apa Itu Matematika Cpctc
4/5CPCTCCPCTC
Bagian-Bagian Segitiga yangSebangun yang Bersesuaian adalah Kongruen Artinya, jika dua segitiga diketahui kongruen, maka semua sudut/sisi yang bersesuaian juga kongruen. Sebagai contoh , jika 2 segitiga kongruen dengan SSS, maka kita juga tahu bahwa sudut dari 2 segitiga adalah kongruen.
Selanjutnya, apa definisi segitiga kongruen? Segitiga Kongruen . Jika dua segitigakongruen maka ketiga sisinya akan sama persis dan ketiga sudutnya sama persis. Sisi dan sudut yang sama mungkin tidak berada pada posisi yang sama , tetapi ada.
Selain di atas, apakah BPK merupakan teorema?
1 Jawaban. Ini adalah teorema yang langsung mengikuti dari definisi kongruensi , Dari Wikipedia: “Dua segitiga kongruen jika sisi-sisi yang bersesuaian sama panjang dan sudut-sudut yang bersesuaian sama besar.”
Apakah garis paralel kongruen?
Jika dua garis sejajar dipotong oleh garis transversal, maka sudut-sudut yang bersesuaian adalah kongruen . Jika dua garis dipotong oleh garis transversal dan sudut-sudut yang bersesuaian kongruen , maka garis-garis tersebut sejajar . Sudut-sudut Dalam pada Sisi yang Sama dari Garis Transversal: Nama adalah deskripsi dari “lokasi” dari sudut-sudut ini.
How Do You Prove Cpctc Using Sas Criterion
In SAS triangle congruence the two corresponding sides and the included angle are equal. In other words, the two triangles are said to be congruent if two corresponding sides and the included angle are equal. Thus, when two triangles are congruent then according to CPCTC the other corresponding side and the other two corresponding angles are also equal.
Also Check: What Is Standard Temperature In Chemistry
What Is Cpctc Math
What exactly is Cpctc math? Corresponding Parts of Congruent Triangles are Congruent, according to the abbreviation CPCTC.
This means that when two or more triangles are congruent, their corresponding sides and angles will also be congruent or equal in measurements. What exactly is Cpctc and how does it work? It means that if two trangles are found to be congruent, all of the corresponding angles and sides are congruent as well. We know that the angles of two triangles are congruent if two triangles are congruent by SSS.
Is Cpctc a synonym for SSS? CPCTC is an acronym for a statement about congruent triangles that sounds like a top-secret government department: Corresponding Parts of Congruent Triangles Are Congruent. These triangles are congruent by SSS using the Reflexive Property for the shared side. What exactly is Cpcte?
Corresponding Parts of Congruent Triangles Are Equal stands for Corresponding Parts of Congruent Triangles Are Equal.
What Is An Sss Triangle
When two triangles are congruent, all three pairs of corresponding sides are congruent and all three pairs of corresponding angles are congruent. If all three pairs of corresponding sides are congruent, the triangles are congruent. This congruence shortcut is known as side-side-side .
How do you prove Cpctc?
Whenever you see two triangles that share a side or an angle, that side or angle belongs to both triangles. With the Reflexive Property, the shared side or angle becomes a pair of congruent sides or angles that you can use as one of the three pairs of congruent things that you need to prove the triangles congruent.
Is aas a congruence theorem?
The AAS Theorem says: If two angles and the non-included side of one triangle are congruent to the corresponding parts of another triangle, the triangles are congruent. Notice how it says non-included side, meaning you take two consecutive angles and then move on to the next side .
Also Check: How To Write Organic Chemistry Lab Report
What Is Cpctc And Example
Corresponding Parts of Congruent Triangles are Congruent It means that if two trangles are known to be congruent , then all corresponding angles/sides are also congruent. As an example, if 2 triangles are congruent by SSS, then we also know that the angles of 2 triangles are congruent.
What does a Cpctc look like?
CPCTC is commonly used at or near the end of a proof which asks the student to show that two angles or two sides are congruent. It means that once two triangles are proven to be congruent, then the three pairs of sides that correspond must be congruent and the three pairs of angles that correspond must be congruent.
What can you say about Cpctc?
Congruent Triangles On A Sphere
As with plane triangles, on a sphere two triangles sharing the same sequence of angle-side-angle are necessarily congruent . This can be seen as follows: One can situate one of the vertices with a given angle at the south pole and run the side with given length up the prime meridian. Knowing both angles at either end of the segment of fixed length ensures that the other two sides emanate with a uniquely determined trajectory, and thus will meet each other at a uniquely determined point thus ASA is valid.
The congruence theorems side-angle-side and side-side-side also hold on a sphere in addition, if two spherical triangles have an identical angle-angle-angle sequence, they are congruent .
The plane-triangle congruence theorem angle-angle-side does not hold for spherical triangles. As in plane geometry, side-side-angle does not imply congruence.
Read Also: Why Geography Matters More Than Ever Chapter 1
Determining Congruence Of Polygons
For two polygons to be congruent, they must have an equal number of sides . Two polygons with n sides are congruent if and only if they each have numerically identical sequences side-angle-side-angle-… for n sides and n angles.
Congruence of polygons can be established graphically as follows:
- First, match and label the corresponding vertices of the two figures.
- Second, draw a vector from one of the vertices of the one of the figures to the corresponding vertex of the other figure. Translate the first figure by this vector so that these two vertices match.
- Third, rotate the translated figure about the matched vertex until one pair of corresponding sides matches.
- Fourth, reflect the rotated figure about this matched side until the figures match.
If at any time the step cannot be completed, the polygons are not congruent.
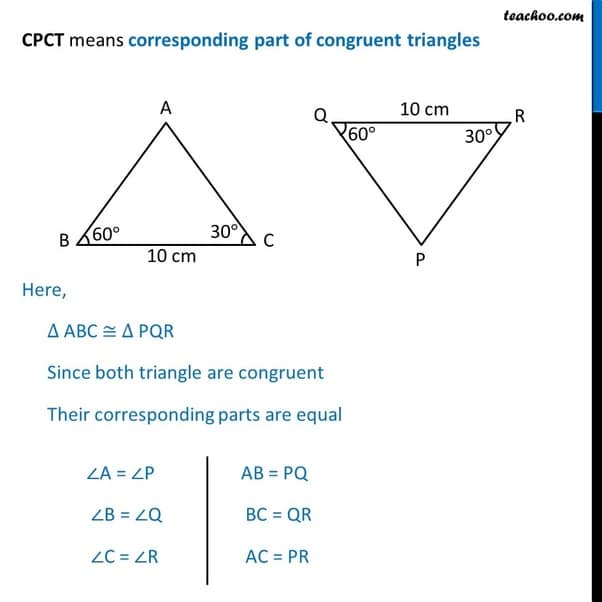
What Is An Example Of Cpctc
The theorem CPCTC tells that when two triangles are congruent then their corresponding sides and angles are also said to be congruent. For example, triangle ABC and triangle PQR are congruent triangles therefore according to the theorem the sides AB = PQ, BC = QR, and CA = RP. Also A = P, B = Q, and C = R.
You May Like: What Grades Do You Need To Study Psychology
What Is Cpctc
The abbreviation CPCTC is for Corresponding Parts of Congruent Triangles are Congruent. The CPCTC theorem states that when two triangles are congruent, then every corresponding part of one triangle is congruent to the other. This means, when two or more triangles are congruent then their corresponding sides and angles are also congruent or equal in measurements. Let us understand the meaning of congruent triangles and corresponding parts in detail.
Congruent Triangles
Two triangles are said to be congruent if they have exactly the same size and the same shape. Two congruent triangles have three equal sides and equal angles with respect to each other.
Corresponding Parts
Corresponding sides mean the three sides in one triangle are in the same position or spot as in the other triangle. Corresponding angles mean the three angles in one triangle are in the same position or spot as in the other triangle.
In the given figure, ABC LMN. It means that the three pairs of sides and three pairs of angles of ABC are equal to the three pairs of corresponding sides and three pairs of corresponding angles of LMN.