How To Add Two Vectors Physics
Adding two vectors A and B graphically can be visualized like two successive walks, with the vector sum being the vector distance from the beginning to the end point. Representing the vectors by arrows drawn to scale, the beginning of vector B is placed at the end of vector A. The vector sum R can be drawn as the vector from the beginning to the end point.
Vector Addition: Triangle Parallelogram And Polygon Law Of Vectors
As already discussed, vectors cannot be simply added algebraically. Following are a few points to remember while adding vectors:
- Vectors are added geometrically and not algebraically.
- Vectors whose resultant have to be calculated behave independently of each other.
- Vector Addition is nothing but finding the resultant of a number of vectors acting on a body.
- Vector Addition is commutative. This means that the resultant vector is independent of the order of vectors.
Making The Coordinate System Work For You
There are many problems in physics and other fields where changing from one coordinate system to a more convenient one makes solving a problem simpler and more intuitive. One example is a mass on an inclined plane. The problem is shown in panel 1. The only force that makes the ball roll down the ramp is the force of gravity, Fg. The trouble is that Fg is at an odd angle to the ramp. But we can impose a different coordinate system upon the problem, a more convenient one in which the x-axis is classed along the ramp and the y-axis perpendicular to it . In this case, we can resolve the Fg vector into its Fgx and Fgy components .
Panels 4, 5 & 6 show ramps of increasing steepness. Notice that the component of Fg pointing down the ramp in each increases with the steepness. The larger force accounts for the fact that the ball will roll faster as the ramp steepens.
Don’t Miss: Practice 2-4 Reasoning In Algebra Answers
Multiplying Vectors By A Scalar
Vectors are geometric representations of magnitude and direction which are often represented by straight arrows, starting at one point on a coordinate axis and ending at a different point. All vectors have a length, called the magnitude, which represents some quality of interest so that the vector may be compared to another vector. Vectors, being arrows, also have a direction. This differentiates them from scalars, which are mere numbers without a direction.
Video advice: Addition of Vectors By Means of Components Physics
This physics video tutorial focuses on the addition of vectors by means of components analytically. It explains how to find the magnitude and direction of the resultant force vector. This video contains all of the formulas and equations needed to resolve a vector into its components and to use that in order to find the magnitude and direction angle of the resultant force vector. This video explains how to add 2 force vectors to get the resultant sum. This tutorial contains plenty of examples and practice problems.
Resolving Vectors Into Components

We know that we can add two vectors to get another. Very often we need to find two convenient vectors that add to a vector of interest. This is called resolving a vector into components.
The example at right shows a vector drawn on a Cartesian plane. By drawing the dashed lines from the tip of the vector to the axes, at right angles, we come up with the vectors Vx and Vy, which sum to vector V.
As we’ll see, resolving V into two vectors that lie along our coordinate axes will be a big help in solving some problems.
Recommended Reading: How Did The Geography Of Greece Affect Its Development
Adding Vectors Graphically: Getting From Here To There
In a previous lesson, we saw the following picture, involving vectors \, \, and \. If we started at the origin, followed vector \, then followed vector \, we would end up at point B. This is the same location we would have ended up at if we had simply followed vector \.
We could state this more clearly if we had simply said the following
This notation really means what we said above. It is just a whole lot easier to say. Following one vector then another is like adding the two vectors together.
Notice that the length of vector B is shorter than the combined lengths of vector A and vector d. This is a clue that we cant just add vectors like we do numbers. We will investigate this soon.
Your Jove Unlimited Free Trial
Fill the form to request your free trial.
We use/store this info to ensure you have proper access and that your account is secure. We may use this info to send you notifications about your account, your institutional access, and/or other related products. To learn more about our GDPR policies click here.
If you want more info regarding data storage, please contact .
You May Like: How Did Geography Impact Ancient Greece
Introduction To Vector In Physics
Simply put, vectors are those physical quantities that have values as well as specific directions. Such as displacement, velocity, etc.
That is, you need to describe the direction of the quantity with the measurable properties of the physical quantity here.
For example, many of you say that the velocity of a particle is five. Since velocity is a vector quantity, just mentioning the value is not a complete argument. You need to specify the direction along with the value of velocity. So, you have to say that the value of velocity in the specified direction is five.
Graphically, a vector is represented by an arrow. Here, the vector is represented by ab. That is, the value of the given vector will depend on the length of the ab vector. And a is the initial point and b is the final point.
Analytically, a vector is represented by an arrow above the letter. And the value of the vector is always denoted by the mod
The Ideal Strategy For Physics Vector
You have to make sure you take all these aspects under consideration before its possible to pick the cost of the Westminster houses for sale youre going to purchase. But if I was giving you address about a marriage feature, I am going to have to provide you the time together with the place. The ideal way to judge a propertys value ought to be based on important factors like the place, the range of bedrooms and the total price.
Also Check: Algebra 2 Puzzle
Adding And Subtracting Vectors
from
Graphical Addition of Vectors: The head-to-tail method of vector addition requires that you lay out the first vector along a set of coordinate axes. Next, place the tail of the next vector on the head of the first one. Draw a new vector from the origin to the head of the last vector. This new vector is the sum of the original two.
Vector Addition Lesson 1 of 2: Head to Tail Addition Methodopposite
What To Do About Physics Vector Before It Is Too Late
The expression relativistic mass is hardly ever used, and therefore, to prevent confusion, I wont mention it here. Because of this, its essential that you get a comfortable grasp of the method of representing and describing vector quantities. Implicit inside this axiom is the notion that the sample space is everything feasible for our probability experiment and that there arent any events outside the sample space. Since the precise frequency of light emitted is affected by the strength of the community electric field, this gave the researchers a means to gauge the strength of the area. For the interest of brevity, I will handwave over the presence of a perfect triangle with our projection vector.
Vector subtraction utilizing perpendicular components is quite similarit is only the accession of a negative vector. pay for essay reviews If youre given the elements of a vector and asked for the direction, you will want to un-do one of the previous few equations. Vectors that arent at nice angles want to be handled.
Also Check: Old Lawyers Never Die They Just Math Worksheet
Adding More Than Two Vectors
Using the head-to-tail method to add more than two vectors is very easy, graphically or numerically . One thing that often confuses students is whether, during the addition process, vectors can cross. They can.
Below is an example of a four-vector addition done in head-to-tail fashion, in which vectors cross. It’s fine, no problem.
Adding more than two vectors with the parallelogram method is more cumbersome. You’d have to do the first addition to come up with a resultant vector, then add that to the next vector to find the new resultant, and so on.
Another thing that the head to tail method shows is that vector addition is commutative. Look at the six ways to add three vectors in the panel below. All six yield, graphically, the same resultant vector R.
Can The Sum Of Two Vectors Have A Zero
Yes, two vectors with equal magnitude and pointing in opposite directions will have sum equal to zero.
Put your understanding of this concept to test by answering a few MCQs. Click Start Quiz to begin!
Select the correct answer and click on the Finish buttonCheck your score and answers at the end of the quiz
Don’t Miss: Simplifying Radicals Worksheet Kuta
How Do You Add Vectors A And B
0:225:04Adding and Subtracting Vectors – YouTubeYouTubeStart of suggested clipEnd of suggested clipAnd direction so magnitude and direction. But what you want to do is you want to take these vectorsMoreAnd direction so magnitude and direction. But what you want to do is you want to take these vectors and you want to put them in such a way that where one vector ends. The other vector begins.
Addition And Subtraction Of Vectors
In Physics, vector quantities are quantities that have a magnitude and direction. It is important to understand how operations like addition and subtraction are carried out on vectors. In this chapter, we will learn about these quantities and their addition and subtraction operations. Let us begin with the addition of vectors.
Don’t Miss: Unit 1 Study Guide Geometry Basics Answer Key
Vector Addition And Subtraction: Graphical Methods
Recall that a vector is a quantity that has magnitude and direction. For example, displacement, velocity, acceleration, and force are all vectors. In on
Teacher SupportTeacher SupportUse the Look At Your Understanding inquiries to assess whether students attain the learning objectives with this section. If students are battling having a specific objective, the Look At Your Understanding can help identify which objective causes the issue and direct students towards the relevant content.
In two dimensions, a vector describes motion in two perpendicular directions, such as vertical and horizontal. For vertical and horizontal motion, each vector is made up of vertical and horizontal components. In a one-dimensional problem, one of the components simply has a value of zero. For two-dimensional vectors, we work with vectors by using a frame of reference such as a coordinate system. Just as with one-dimensional vectors, we graphically represent vectors with an arrow having a length proportional to the vectors magnitude and pointing in the direction that the vector points.
Video advice: Adding Vectors A Level Physics
This video explains adding vectors, both mathematically and graphically for A Level Physics.
What Is The Triangle Law Of Addition Of Vectors
The triangle law of the addition of vectors states that two vectors can be added together by placing them together in such a way that the first vectors head joins the tail of the second vector. Thus, by joining the first vectors tail to the head of the second vector, we can obtain the resultant sum vector.
Don’t Miss: Half Life Chemistry Equation
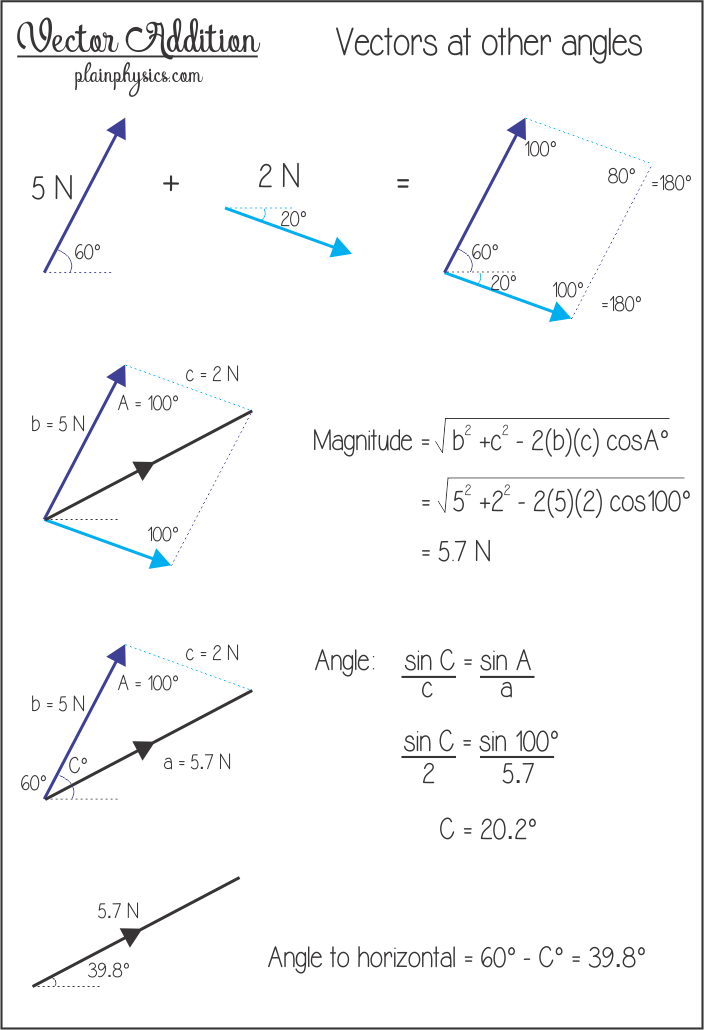
Some Special Cases Of Vector Addition
The following are some special cases to make vector calculation easier to represent.
1. =0° : Here is the angle between the two vectors. That is, if the value of is zero, the two vectors are on the same side. In this case, the value of the resultant vector will be
Thus, the absolute value of the resultant vector will be equal to the sum of the absolute values of the two main vectors. Notice the image below
2. =180° : Here, if the angle between the two vectors is 180°, then the two vectors are opposite to each other. That is, the value of cos here will be -1.
Here the absolute value of the resultant vector is equal to the absolute value of the subtraction of the two vectors. And the resultant vector will be oriented towards it whose absolute value is higher than the others.
3. a=b and =180° : Here the two vectors are of equal value and are in opposite directions to each other. In this case, the absolute value of the resultant vector will be zero. That is, the resolution vector is a null vector
2. =90° : If the angle between the two vectors is 90 degrees. The value of cos will be zero. So, here the resultant vector will follow the formula of Pythagoras
In this case, the two vectors are perpendicular to each other. And the resultant vector will be located at the specified angle with the two vectors. Suppose, here two vectors a, b are taken and the resultant vector c is located at angle with a vector Then the direction of the resultant vector will be
Polygon Law Of Vector
According to the polygon law of vector addition, if the number of vectors can be represented in magnitude and direction by the sides of a polygon taken in the same order, then their resultant is represented by magnitude and direction such that the closing side of the polygon is taken in the opposite direction.Let
You May Like: Kendall Hunt Geometry
What Is A Vector
From a mathematical point of view, a vector is an ordered sequence of numbers , and that’s all there is to it. Of course, scientists wouldn’t be themselves if they left it at that, so they expanded this definition. In general, a vector is an element of a vector space, period. This explanation seems simple enough until we learn that for mathematicians, vector spaces can consist of sequences, functions, permutations, matrices, etc. Fortunately, we need none of that in this vector addition calculator.
On the other hand, physicists prefer to think of vectors as arrows that are attached to objects. As such, they represent forces that act upon the thing, be it gravitation, speed, or magnetic pull. The direction of such an arrow tells us the force’s… well, direction, while its length indicates how large of a force it is.
Fortunately, both approaches boil down to essentially the same thing, at least in our case and the vector addition calculator. Still, we can represent vectors in two ways: using Cartesian coordinates or the magnitude and angle. However, the latter is possible only in the two-dimensional case since it corresponds, in fact, to having polar coordinates.
Alternatively, we can represent the two-dimensional vector v using its magnitudem and direction θ. The first one is simply the vector’s length. The latter is the angle going counterclockwise from the positive half of the horizontal axis to the vector when drawn on the plane with the start point in .
What Is The Addition Of Vectors
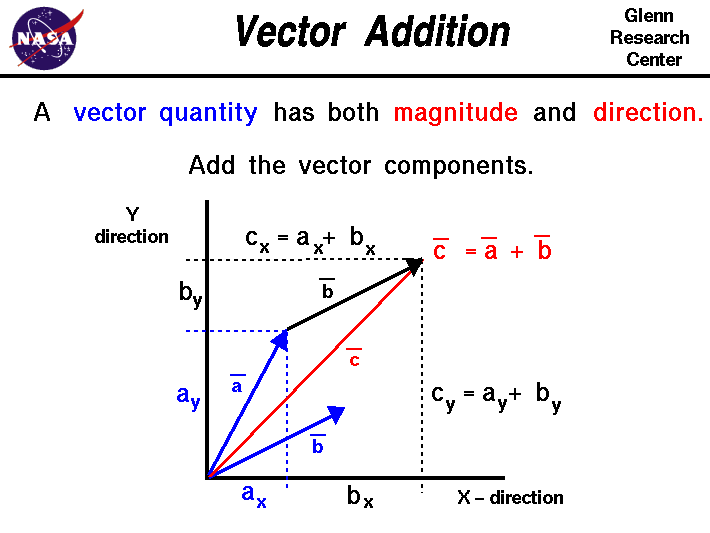
The addition of vectors means putting two or more vectors together. In the addition of vectors, we are adding two or more vectors using the addition operation in order to obtain a new vector that is equal to the sum of the two or more vectors.Two vectors, a and b, can be added together using vector addition, and the resultant vector can be written as: a + b.
Example: Given two vectors, a = and b = , the sum of these two vectors is
Read Also: Geometry Workbook Answers Mcgraw Hill
Browse More Topics Under Motion In A Plane
You can download Motion in a Plane Cheat Sheet by clicking on the download button below
The characteristics of vectors are as follows
- They possess both magnitudes as well as direction.
- They do not obey the ordinary laws of Algebra.
- These change if either the magnitude or direction change or both change.
- Vectors are significantly represented by the bold-faced letters or letter which have an arrow over them.
Resolving A Vector Into Components
In the examples above, we have been adding vectors to determine the resultant vector. In many cases, however, we will need to do the opposite. We will need to take a single vector and find what other vectors added together produce it. In most cases, this involves determining the perpendicular components of a single vector, for example the x– andy-components, or the north-south and east-west components.
For example, we may know that the total displacement of a person walking in a city is 10.3 blocks in a direction .0º north of east and want to find out how many blocks east and north had to be walked. This method is called finding the components of the displacement in the east and north directions, and it is the inverse of the process followed to find the total displacement. It is one example of finding the components of a vector. There are many applications in physics where this is a useful thing to do. We will see this soon in Projectile Motion, and much more when we coverforces in Dynamics: Newtons Laws of Motion. Most of these involve finding components along perpendicular axes , so that right triangles are involved. The analytical techniques presented in Vector Addition and Subtraction: Analytical Methods are ideal for finding vector components.
PHET EXPLORATIONS: MAZE GAME
Read Also: Who Is Paris Jackson’s Biological Father