Semiempirical Formula For Nuclear Binding Energy
For a nucleus with A nucleons, including Z protons and N neutrons, a semi-empirical formula for the binding energy per nucleon is:
- BE
4 } is purely empirical it is + for even-even nuclei and – for odd-odd nuclei. When A is odd, the pairing term is identically zero.
ZNZ
Measurement Of Mass Defect In Atomic And Molecular Reactions
A typical chemical reaction might involve a nett energy of 30 kJ per mole, or 5 x 10-20 J per molecule. So the change in mass is 5 x 10-37 kg, which is only .0001% of the mass of an electron. These defects are small, so we should need a very precise method of measuring mass , such as mass spectrometry or a Penning trap, and/or a bigger defect to measure. Precise measurement means that all components in the reaction must be charged, so a simple example would be He++ + e He+. But we could also make the effect bigger by using a highly charged ion. To take an extreme case , consider the reactionAu79+ + e Au78+. Here we have the advantage that the potential energy of the electron close to that highly charged gold nucleus is extremely negative. Consequently, the mass defect is large: of the same order as the electron mass.
Studies of highly charged ions are regularly performed because the optical transitions between electron states in these ions can be measured very precisely to produce extremely precise time measurements and to test fundamental theories of physics.
Positronium might seem to be another candidate for measuring a purely electric or chemical binding energy. However, it is not stable enough to allow the precision needed .
For more discussion, see this link. And to see why the neutron and proton attract, see Why there would be no chemistry without relativity. And the example of mass defect in power stations is here.
The Nuclear Potential Well
In our development of a model of the nucleus we have so far not considered the nuclear binding energy. Let us imagine the situation wherein a neutron of low kinetic energy approaches a nucleus . Since the neutron is uncharged it is not affected by the Coulomb field of the nucleus and approaches the nucleus with no interaction, until it is close enough to experience the strong nuclear force Fn, which is always attractive, i.e. Fn is a positive quantity. At the point rn the neutron experiences the strong attraction to the nucleus and is absorbed. The surface of the nucleus is assumed to extend to rs since this distance represents the radius of the nucleus over which the nuclear force is constant. When the neutron is absorbed, energy is released and emitted in the form of a -quantum. The energy of the -ray can be calculated from the known masses of the reactants and product nuclides: E = 931.5.
FIG. 11.1. The approach along the x– axis of a neutron towards a nucleus leading to the neutron being trapped at a certain energy level, EB . Fnucl is the nuclear force extending from the surface of the solid core at rs to the distance rn. EB is the nuclear binding energy in the potential well.
MARIA GOEPPERT MAYER, … D. JENSEN, in, 1968
Don’t Miss: Can Work Be Negative Physics
Electron Binding Energy Ionization Energy
Electron binding energy which is also commonly known as ionization energy is the energy required to remove an electron from its atomic orbital. The electron binding energy is mostly derived as a result of the electromagnetic interaction that occurs between the electron and the nucleus, the other electrons of the atom, molecule or solid that is usually mediated by photons.
Nuclear Binding Energy Curve
In the periodic table of elements, the series of light elements from hydrogen up to sodium is observed to exhibit generally increasing binding energy per nucleon as the atomic mass increases. This increase is generated by increasing forces per nucleon in the nucleus, as each additional nucleon is attracted by other nearby nucleons, and thus more tightly bound to the whole. Helium-4 and oxygen-16 are particularly stable exceptions to the trend . This is because they are doubly magic, meaning their protons and neutrons both fill their respective nuclear shells.
The region of increasing binding energy is followed by a region of relative stability in the sequence from magnesium through xenon. In this region, the nucleus has become large enough that nuclear forces no longer completely extend efficiently across its width. Attractive nuclear forces in this region, as atomic mass increases, are nearly balanced by repellent electromagnetic forces between protons, as the atomic number increases.
Finally, in elements heavier than xenon, there is a decrease in binding energy per nucleon as atomic number increases. In this region of nuclear size, electromagnetic repulsive forces are beginning to overcome the strong nuclear force attraction.
Also Check: What Happened To Beth Thomas Biological Father
Types Of Binding Energy
There are several types of binding energy, each operating over a different distance and energy scale. The smaller the size of a bound system, the higher its associated binding energy.
A bound system is typically at a lower energy level than its unbound constituents because its mass must be less than the total mass of its unbound constituents. For systems with low binding energies, this “lost” mass after binding may be fractionally small, whereas for systems with high binding energies, the missing mass may be an easily measurable fraction. This missing mass may be lost during the process of binding as energy in the form of heat or light, with the removed energy corresponding to the removed mass through Einstein’s equation E = mc2. In the process of binding, the constituents of the system might enter higher energy states of the nucleus/atom/molecule while retaining their mass, and because of this, it is necessary that they are removed from the system before its mass can decrease. Once the system cools to normal temperatures and returns to ground states regarding energy levels, it will contain less mass than when it first combined and was at high energy. This loss of heat represents the “mass deficit,” and the heat itself retains the mass that was lost . This mass will appear in any other system that absorbs the heat and gains thermal energy.
Binding Energy And Nuclide Masses
| This section does not cite any . Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. |
The fact that the maximum binding energy is found in medium-sized nuclei is a consequence of the trade-off in the effects of two opposing forces that have different range characteristics. The attractive nuclear force , which binds protons and neutrons equally to each other, has a limited range due to a rapid exponential decrease in this force with distance. However, the repelling electromagnetic force, which acts between protons to force nuclei apart, falls off with distance much more slowly . For nuclei larger than about four nucleons in diameter, the additional repelling force of additional protons more than offsets any binding energy that results between further added nucleons as a result of additional strong force interactions. Such nuclei become increasingly less tightly bound as their size increases, though most of them are still stable. Finally, nuclei containing more than 209 nucleons are all too large to be stable, and are subject to spontaneous decay to smaller nuclei.
Nuclear fusion produces energy by combining the very lightest elements into more tightly bound elements , and nuclear fission produces energy by splitting the heaviest elements into more tightly bound elements . Both processes produce energy, because middle-sized nuclei are the most tightly bound of all.
You May Like: Ccl4 Geometry
Binding Energy Curve Explanation
We know that the mass of a nucleus is lesser than that of the sum of its constituent protons and neutrons. Now, if we take a glimpse at the same number of protons and neutrons as in the nucleus we were trying to recreate, we find that the total mass of the individual protons and neutrons is always greater than when they are arranged as an individual nucleus.
The difference in the mass between the sum of the products and the sum of the individual nucleons is known as the mass defect. The definition of binding energy per nucleon is the amount of energy required to break the nucleus into protons and neutrons again the larger the binding energy, the more difficult it would be to separate subatomic particles from their nucleus. The figure below shows the binding energy for each element, against their atomic number :
Starting from H2, as we increase the atomic number, the binding energy also increases. So He has a greater binding energy per nucleon than the binding energy of hydrogen while Li has greater binding energy than Helium, and Beryllium has greater binding energy than Lithium, and so on. We observe that this trend continues till we reach iron. After that, it begins to decrease slowly.
Calculation Of Nuclear Binding Energy
Nuclear binding energy can be calculated following steps:
i) Obtain the mass defect
ii) Once the mass defect is known, the nuclear binding energy can be obtained by converting that mass to energy using the
Formula Eb= c2 ,
where mass is unit of kgs
iii) Now once the energy obtained is known, it is to be converted into per-nucleon and per- mole quantities.
Example: For finding the mass defect and Nuclear Binding Energy of a copper-63 nucleus if the actual mass of a copper-63 nucleus is given as 62.91367 amu.
Copper atoms have 29 protons and copper-63 also has 34 neutrons.
Since the mass of a proton is 1.00728 amu and a neutron is 1.00867 amu.
The combined mass is calculated:
29 protons + 34 neutrons
or 63.50590 amu
Recommended Reading: Does Kamala Harris Have Any Biological Children
Mass Energy Main Points
- Einsteins famous mass-energy equivalence, i.e, E=mc2, defines the relationship between mass of a particle and energy. Here, E is the energy that is equivalent to the product of m that is mass and the speed of light squared. The speed of light is almost equal to 3 X 108 meters per second.
- Equivalently, the mass of a particle also equals to its Energy divided by the speed of light squared, i.e, m = E / c2.
- As per the formula, a little amount of rest mass is capable of generating enormous amount of energy, independent of its matter.
- As per the law of Conservation of Energy, energy is incapable of being created or destroyed. It can only be transferred or transformed into various forms. Taking the example of a dynamic stick explosion, the chemical energy gets transformed into kinetic energy.
- In classical physics, the conservation of energy and the conservation of mass were two unequal phenomenon, however, E=mc2 infers that mass-energy is conserved as a whole, which goes on to prove that any object with mass can be converted to pure energy.
A Structure Of The Atom
The atoms of which every element of matter is composed have a nucleus at the center and electrons whirling about this nucleus that can be visualized as planets circling around a sun, though it is impossible to locate them precisely within the atom. The nuclei of atoms are composed of protons, which have a positive electrical charge, and neutrons, which are electrically neutral. Electrons are electrically negative and have a charge equal in magnitude to that of a proton.
The number of electrons in an atom is normally equal to the number of protons in the nucleus. As a result, atoms of elements are normally electrically neutral. The mass of an atom lies almost entirely in its nucleus since protons and neutrons are far heavier than electrons.
Free neutrons are unstable particles which decay naturally into a proton and electron, with a half-life of about 12 minutes.
neutron ===> proton + electron + a neutrino
Read Also: Eoc Fsa Warm Ups Algebra 1 Answers
Graph Of Binding Energy Per Nucleon
In nuclear physics, one of the most important experimental quantities is the binding energy per nucleon , which is defined by
This quantity is the average energy required to remove an individual nucleon from a nucleusanalogous to the ionization energy of an electron in an atom. If the BEN is relatively large, the nucleus is relatively stable. BEN values are estimated from nuclear scattering experiments.
A graph of binding energy per nucleon versus atomic number A is given in . This graph is considered by many physicists to be one of the most important graphs in physics. Two notes are in order. First, typical BEN values range from 610 MeV, with an average value of about 8 MeV. In other words, it takes several million electron volts to pry a nucleon from a typical nucleus, as compared to just 13.6 eV to ionize an electron in the ground state of hydrogen. This is why nuclear force is referred to as the strong nuclear force.
Second, the graph rises at low A, peaks very near iron and then tapers off at high A. The peak value suggests that the iron nucleus is the most stable nucleus in nature . The reason the graph rises and tapers off has to do with competing forces in the nucleus. At low values of A, attractive nuclear forces between nucleons dominate over repulsive electrostatic forces between protons. But at high values of A, repulsive electrostatic forces between forces begin to dominate, and these forces tend to break apart the nucleus rather than hold it together.
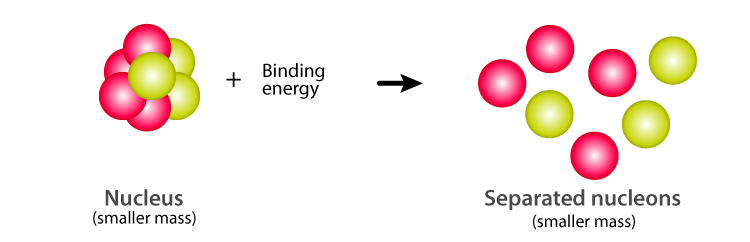
Nuclear Binding Energy And Mass Defect
- Calculate the mass defect and nuclear binding energy of an atom
Key Points
- Nuclear binding energy is the energy required to split a nucleus of an atom into its components.
- Nuclear binding energy is used to determine whether fission or fusion will be a favorable process.
- The mass defect of a nucleus represents the mass of the energy binding the nucleus, and is the difference between the mass of a nucleus and the sum of the masses of the nucleons of which it is composed.
Terms
- nucleonOne of the subatomic particles of the atomic nucleus, i.e. a proton or a neutron.
- mass defectThe difference between the calculated mass of the unbound system and the experimentally measured mass of the nucleus.
- strong forceThe nuclear force, a residual force responsible for the interactions between nucleons, deriving from the color force.
You May Like: Demon Guardian Geometry Dash
Example Values Deduced From Experimentally Measured Atom Nuclide Masses
The following table lists some binding energies and mass defect values. Notice also that we use 1 u = MeV. To calculate the binding energy we use the formula Z + N mn â mnuclide where Z denotes the number of protons in the nuclides and N their number of neutrons. We takemp = MeV, me = MeV and mn = MeV. The letter A denotes the sum of Z and N . If we assume the reference nucleon has the mass of a neutron we could define the total binding energy as the difference from the mass of the nucleus, and the mass of a collection of A free neutrons. In other words, it would be mn â mnuclide. The “total binding energy per nucleon” would be this value divided by A.
| nuclide | |
|---|---|
| 545.281 MeV | 8.7948 MeV |
| nuclide | |
|---|---|
| 7.7181 MeV | 2.5727 MeV |
In the table above it can be seen that the decay of a neutron, as well as the transformation of tritium into helium-3, releases energy hence, it manifests a stronger bound new state when measured against the mass of an equal number of neutrons . Such reactions are not driven by changes in binding energies as calculated from previously fixed N and Z numbers of neutrons and protons, but rather in decreases in the total mass of the nuclide/per nucleon, with the reaction.
Things Great And Small
Nuclear Decay Helps Explain Earths Hot Interior
A puzzle created by radioactive dating of rocks is resolved by radioactive heating of Earths interior. This intriguing story is another example of how small-scale physics can explain large-scale phenomena.
Radioactive dating plays a role in determining the approximate age of the Earth. The oldest rocks on Earth solidified about 3.5×109 years agoa number determined by uranium-238 dating. These rocks could only have solidified once the surface of the Earth had cooled sufficiently. The temperature of the Earth at formation can be estimated based on gravitational potential energy of the assemblage of pieces being converted to thermal energy. Using heat transfer concepts discussed in Thermodynamics it is then possible to calculate how long it would take for the surface to cool to rock-formation temperatures. The result is about 109 years. The first rocks formed have been solid for 3.5×109 years, so that the age of the Earth is approximately 4.5 × 109 years. There is a large body of other types of evidence that supports this age. The puzzle is that, given its age and initial temperature, the center of the Earth should be much cooler than it is today .
You May Like: Michael Jackson Kids Biological
Binding Energy Formula: Mass Defect Solved Examples
Binding energy is defined as the energy corresponding to a mass defect. A nucleus resembles an inflexible spherical ball formed by assembling a large number of tiny spherical balls known as nucleons. A gluing agent is needed to bind the nucleons that have been gathered. To transfer the energy resulting in a mass defect, each nucleon must contribute some of its mass. The energy required to break down a nucleus into its constituent nucleons is known as its binding energy. In this article, we will have a look at the formula of binding energy, mass defect, and some sample questions.
|
Table of Content |