List Of Words That Start With B
Ball – a sphere together with its interior.
Bar Graph – a diagram showing a system of connections or interrelations between two or more things by using bars.
Base – the number on which the rate is estimated the side that forms a right angle with the height of an object.
Base Depth of the Triangular Prism – the perpendicular distance from the base of a triangle to the top of the triangle.
Base of the Triangular Prism – the triangular end of the prism.
Basic arithmetic operations – addition, subtraction, multiplication, and division.
Bayess Rule – a rule for finding conditional probability.
Biannual – twice a year.
- Morning work. Remote learning packets.
- Most need no answer key or key is included.
- Videos for audio learners. God bless headphones!
See free teacher, homeschool, digital interactive school-at-home learning exercises with no login, no sign-up, no voucher, no account, and no credit card. Loads of digital activities for device-based learning. As seen at TeachersPayTeachers.
Bias – favoring one choice over another in a survey.
Bijection – a one-to-one function.
Bill – a written statement of the purchase or sale of goods.
Bimodal – having two modes, which are the most frequently occurring number in a list.
Binary – base 2 which means that it uses just two digits: 0 and 1.
Binary Number – a number written to base 2.
Binary Operation – a binary operation is an operation that involves two operands. For example, addition and subtraction are binary operations.
Algebra Formulas For Class 10
An important algebra formula introduced in class 10 is the quadratic formula. The general form of the quadratic equation is ax2 + bx + c = 0, and there are two methods of solving this quadratic equation. The first method is to solve the quadratic equation by the algebraic method, and the second method is to solve through the use of the quadratic formula. The below formula is helpful to quickly find the values of the variable x with the least number of steps.
In the above expression, the value b2 – 4ac is called the determinant and is useful to find the nature of the roots of the given equation. Based on the value of the determinant, the three types of roots are given below.
- If b2 – 4ac > 0, then the quadratic equation has two distinct real roots.
- If b2 – 4ac = 0, then the quadratic equation has two equal real roots.
- If b2 – 4ac < 0, then the quadratic equation has two imaginary roots.
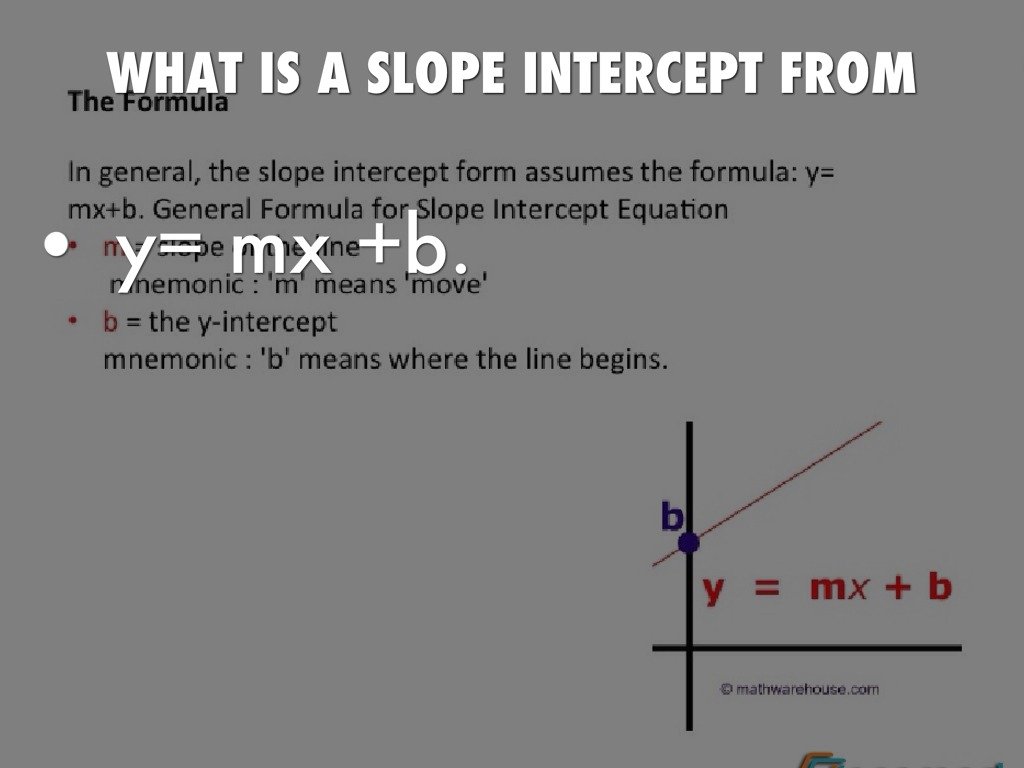
Example: Y = 2x + 1 Is A Linear Equation:
The graph of y = 2x+1 is a straight line
- When x increases, y increases twice as fast, so we need 2x
- When x is 0, y is already 1. So +1 is also needed
- And so: y = 2x + 1
Here are some example values:
| x | |
|---|---|
| y = 2 × + 1 = -1 | |
| 0 | y = 2 × 0 + 1 = 1 |
| 1 | y = 2 × 1 + 1 = 3 |
| 2 | y = 2 × 2 + 1 = 5 |
Check for yourself that those points are part of the line above!
Don’t Miss: Prefix Cyte
Bsc Mathematics Admission Process
The admission to the students for BSc Mathematics is granted on the performance basis and their overall scores in 10+2 level while some take an entrance test to select the eligible students for the course. Admission process generally varies across colleges so the students must visit the official website for accurate information.
After qualifying the entrance exams, the shortlisted students need to appear for a Group Discussion and Personal Interview round as well so that the examiner can get to know more about them.
Notation Language And Rigor
Most of the mathematical notation in use today was not invented until the 16th century. Before that, mathematics was written out in words, limiting mathematical discovery.Euler was responsible for many of the notations in use today. Modern notation makes mathematics much easier for the professional, but beginners often find it daunting. According to Barbara Oakley, this can be attributed to the fact that mathematical ideas are both more abstract and more encrypted than those of natural language. Unlike natural language, where people can often equate a word with the physical object it corresponds to, mathematical symbols are abstract, lacking any physical analog. Mathematical symbols are also more highly encrypted than regular words, meaning a single symbol can encode a number of different operations or ideas.
Don’t Miss: Mm In Chemistry Stands For
Inspiration Pure And Applied Mathematics And Aesthetics
Mathematics arises from many different kinds of problems. At first these were found in commerce, land measurement, architecture and later astronomy today, all sciences pose problems studied by mathematicians, and many problems arise within mathematics itself. For example, the physicistRichard Feynman invented the path integral formulation of quantum mechanics using a combination of mathematical reasoning and physical insight, and today’s string theory, a still-developing scientific theory which attempts to unify the four fundamental forces of nature, continues to inspire new mathematics.
Some mathematics is relevant only in the area that inspired it, and is applied to solve further problems in that area. But often mathematics inspired by one area proves useful in many areas, and joins the general stock of mathematical concepts. A distinction is often made between pure mathematics and applied mathematics. However pure mathematics topics often turn out to have applications, e.g. number theory in cryptography.
As in most areas of study, the explosion of knowledge in the scientific age has led to specialization: there are now hundreds of specialized areas in mathematics and the latest Mathematics Subject Classification runs to 46 pages. Several areas of applied mathematics have merged with related traditions outside of mathematics and become disciplines in their own right, including statistics, operations research, and computer science.
Symbols That Do Not Belong To Formulas
In this section, the symbols that are listed are used as some sorts of punctuation marks in mathematical reasoning, or as abbreviations of English phrases. They are generally not used inside a formula. Some were used in classical logic for indicating the logical dependence between sentences written in plain English. Except for the first two, they are normally not used in printed mathematical texts since, for readability, it is generally recommended to have at least one word between two formulas. However, they are still used on a black board for indicating relationships between formulas.
- ,
- Used for marking the end of a proof and separating it from the current text. The initialismQ.E.D. or QED is often used for the same purpose, either in its upper-case form or in lower case.
- Bourbaki dangerous bend symbol: Sometimes used in the margin to forewarn readers against serious errors, where they risk falling, or to mark a passage that is tricky on a first reading because of an especially subtle argument.
- Abbreviation of “therefore”. Placed between two assertions, it means that the first one implies the second one. For example: “All humans are mortal, and Socrates is a human. Socrates is mortal.”
- Abbreviation of “because” or “since”. Placed between two assertions, it means that the first one is implied by the second one. For example: “11 is prime it has no positive integer factors other than itself and one.”
Recommended Reading: Beth Thomas Parents
What Are The Types Of Sets
Types of a SetFinite Set. A set which contains a definite number of elements is called a finite set. … Infinite Set. A set which contains infinite number of elements is called an infinite set. … Subset. … Proper Subset. … Universal Set. … Empty Set or Null Set. … Singleton Set or Unit Set. … Equal Set.Plus26 août 2019
Algebra Formulas For Class 8
The algebra formulas for three variables a, b, and c and for a maximum degree of 3 can be easily derived by multiplying the expression by itself, based on the exponent value of the algebraic expression. The below formulas are for class 8.
- 2 = a2 + 2ab + b2
- 2 = a2 – 2ab + b2
- = a2 – b2
- 3 = a3 + 3a2b + 3ab2 + b3
- 3 = a3 – 3a2b + 3ab2 – b3
- a3 + b3 =
- a3 – b3 =
- 2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
Some of the common laws of exponents with the same bases having different powers, and different bases having the same power, are useful to solve complex exponential terms. The higher exponential values can be easily solved without any expansion of the exponential terms. These exponential laws are further useful to derive some of the logarithmic laws.
- am. an = am + n
- a-m = 1/am
Read Also: Edgenuity Answer Key Algebra 1
List Of Mathematical Symbols By Subject
The following list of mathematical symbols by subject features a selection of the most common symbols used in modern mathematical notation within formulas, grouped by mathematical topic. As it is impossible to know if a complete list existing today of all symbols used in history is a representation of all ever used in history, as this would necessitate knowing if extant records are of all usages, only those symbols which occur often in mathematics or mathematics education are included. Many of the characters are standardized, for example in DIN 1302 General mathematical symbols or DIN EN ISO 80000-2 Quantities and units Part 2: Mathematical signs for science and technology.
The following list is largely limited to non-alphanumeric characters. It is divided by areas of mathematics and grouped within sub-regions. Some symbols have a different meaning depending on the context and appear accordingly several times in the list. Further information on the symbols and their meaning can also be found in the respective linked articles.
What Is Mathematics
Mathematics is one of the most important subjects. Mathematics is a subject of numbers, shapes, data, measurements and also logical activities. It has a huge scope in every field of our life, such as medicine, engineering, finance, natural science, economics, etc. We are all surrounded by a mathematical world.
The concepts, theories and formulas that we learn in Maths books have huge applications in real-life. To find the solutions for various problems we need to learn the formulas and concepts. Therefore, it is important to learn this subject to understand its various applications and significance.
You May Like: Redken Acidic Bonder Vs Olaplex
Is /c = A/
This is part of a series on common misconceptions.
True or False?
\frac\right)} = \frac\right)}. c=a.
Why some people say it’s true:Just like with multiplication, the order that you choose to evaluate the two division operations doesn’t matter.
Why some people say it’s false:It’s almost never true. Maybe there are a few very special cases for choosing a c so that it’s true.
\frac\right)} \neq \frac\right)} c=a. Consider the following example:
Does \frac\right)} = \frac\right)} 2=36?
\frac\right)} = \frac = 3. 2=26=3.
\frac\right)} = \frac =12. 36=336=12.
3=12. Therefore, the given equation is false.
\frac\right)} = \frac\right)} c=a:
c all equal 1, then this equation is true. But there are many other examples.
If \frac\right)} = \frac\right)} c=a, then by cross-multiplying, we can simplify to
a c . \begin\frac \times \frac & = a \times c\\\frac & = a \times c\\ \frac & = a \times c\\ \frac & = c.\end ba×cbb×ca×bcac1=a×c=a×c=a×c=c.
The only two values that satisfy the equation 1 1 c=-1 c=1. Therefore, the set of all cases when the original equation is true are those where c 1 c = 1 \text -1 c=1 or 1. The other two variables can take on any values, so long as c
\frac\right)} = \frac\right)} 1=36?
\frac\right)} = \frac = -6. 1=16=6.
\frac\right)} = \frac =-6. 36=636=6.
= is one special case when the given equation is true.
Want to make sure you’ve got this concept down? Try this problem:
Bsc Mathematics Entrance Exams

The candidates can apply for BSc Mathematics post completing 10+2 examination with PCB/PCM/PCMB group. The entrance exams are usually conducted for admission in B.Sc Hons. Mathematics.
Given below are some entrance exams held for admission in BSc Mathematics courses.
| Entrance Exam |
|---|
- Universities
- Scientific Institutes
Besides the above-mentioned sectors, there are many other sectors that hunt for the eligible who have completed BSc Mathematics.
The table below describes some of the few job positions that can be considered by the BSc Mathematics graduates along with the Average Salary Scale:
You May Like: What Happened To Beth Thomas
What Is Equal Set
Equal set definition math states that when two sets have the same and equal elements, they are called Equal Sets. The arrangement or the order of the elements does not matter, only the same elements in each set matter. … An equal set is an equivalent set, but an equivalent set necessarily cannot be an equal set.
Commissioned By Unesco Professor B Transforms Caribbean Teacher Training
Dr. Everard Barrett, the creator and founder of Professor B Math, was commissioned to a UNESCO mission in mathematics education at the request of foreign governments in 1980.
After a captivating presentation to participants of the inaugural seminar held by the United Nations Development Program, Dr. Barrett was invited to complete a pilot project in Jamaica with the intention of enabling primary teachers to pass the qualifying exam in mathematics, which boasted a dismal 20% passing rate.
A national teaching crisis had been solved.
Also Check: Why Was The Pail Pale Answers
Positive Or Negative Slope
Going from left-to-right, the cyclist has to Push on a Positive Slope:
m = â31 = â3
b = 0
We do not need the zero! So:
y = â3x
What is the equation for a vertical line?The slope is undefined … and where does it cross the Y-Axis?
In fact, this is a special case, and we use a different equation, not “y=…”, but instead we use “x=…”.
Like this:
Every point on the line has x coordinate 1.5,that is why its equation is x = 1.5
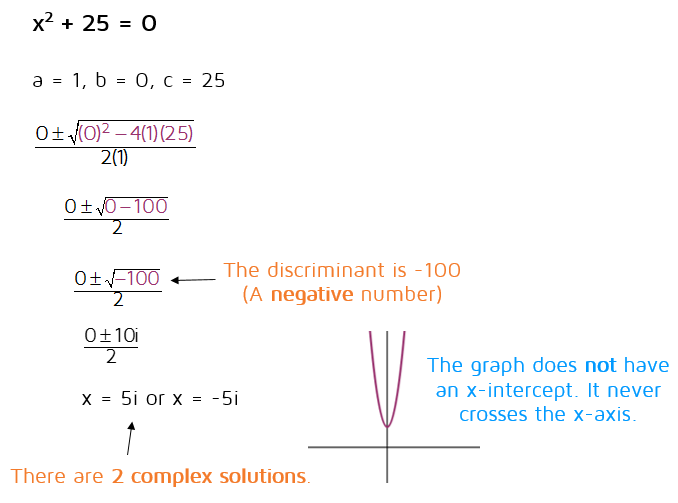
Example : Solve X2 + 4x + 1 = 0
Step 1 can be skipped in this example since the coefficient of x2 is 1
Step 2 Move the number term to the right side of the equation:
Step 3 Complete the square on the left side of the equation and balance this by adding the same number to the right side of the equation.
2 = 2 = 22 = 4
Step 4 Take the square root on both sides of the equation:
Step 5 Subtract from both sides :
Read Also: Geometry Chapter 10 Test Form B Answers
Example: A Plane Is Flying Along Pointing North But There Is A Wind Coming From The North
The two vectors result in a slightly slower ground speed heading a little East of North.
If you watched the plane from the ground it would seem to be slipping sideways a little.
Have you ever seen that happen? Maybe you have seen birds struggling against a strong wind that seem to fly sideways. Vectors help explain that.
Velocity, acceleration, force and many other things are vectors.
Algebra Formulas For Class 9
Logarithms are useful for the computation of highly complex multiplication and division calculations. The normal exponential form of 25 = 32 can be transformed to a logarithmic form as Log 32 to the base of 2 = 5. Further, the multiplication and division between two mathematic expressions can be easily transformed into addition and subtraction, after converting them to logarithmic form. The below properties of logarithms formulas, which are applicable in logarithmic calculations.
You May Like: What Does The Suffix Oxia Mean
Solving General Quadratic Equations By Completing The Square
We can complete the square to solve a Quadratic Equation .
But a general Quadratic Equation can have a coefficient of a in front of x2:
ax2 + bx + c = 0
But that is easy to deal with … just divide the whole equation by “a” first, then carry on:
x2 + x + c/a = 0
Now we can solve a Quadratic Equation in 5 steps:
- Step 1 Divide all terms by a .
- Step 2 Move the number term to the right side of the equation.
- Step 3 Complete the square on the left side of the equation and balance this by adding the same value to the right side of the equation.
We now have something that looks like 2 = q, which can be solved rather easily:
- Step 4 Take the square root on both sides of the equation.
- Step 5 Subtract the number that remains on the left side of the equation to find x.
How To Use Algebraic Expressions Formulas While Solving Problems
We have multiple algebraic expressions formulas and some of them have to be used according to the need while solving the problems. For example, to factorize the expression, 8×3 + 27, we apply the a3 + b3 formula as follows.
a3 + b3 =
Substitute a = 2x and b = 3 on both sides,
3 + 33 = 2 – + 32)
8×3 + 27 = .
Recommended Reading: Paris Michael Katherine Jackson Real Father
What Is The Definition Of Mathematics
Mathematics simply means to learn or to study or gain knowledge. The theories and concepts given in mathematics help us understand and solve various types of problems in academic as well as in real life situations.
Mathematics is a subject of logic. Learning mathematics will help students to grow their problem-solving and logical reasoning skills. Solving mathematical problems is one of the best brain exercises.