What Is Life Span Approach
The Lifespan Developmental Approach has provided an overarching framework for understanding human development from conception to death. … Development unfolds as a process that includes both gains and losses across the lifespan that results in a multidimensional, multidirectional and multifunctional perspective.
Maximum Height Of Projectile
After understanding what is projectile and what is projectile motion, let us know the maximum height of projectile. The maximum height of the object is the highest vertical position along its trajectory. The horizontal displacement of the projectile is called the range of the projectile. The range of the projectile is dependent on the initial velocity of the object.
If v is the initial velocity, g = acceleration due to gravity and H = maximum height in meters, = angle of the initial velocity from the horizontal plane .
The maximum height of projectile is given by the formula:
How Is Bullet Trajectory Determine
If a bullet passes through only ONE object you can determine the bullet’s Trajectory by inserting a Trajectory Rod in the single bullet hole made by the bullet and extending a string to illustrate the bullet’s trajectory path. 1. An accurate sketch showing bullet trajectories at a crime scene can be very useful.
Read Also: Beth From Child Of Rage Now
Where Does Trajectory Come From
The first records of the word trajectory come from the 1660s. It comes from the Latin trjectrius, meaning casting over, from the verb tricere, to cast or to throw over or across. The first part of the word is equivalent to trans-, meaning across, and the root jec comes from the Latin verb jacere, meaning to throw .
Thanks to gravity, what goes up must come down. The path that something follows as it takes the journey up and then down again is its trajectory. When gravity is in play, objects that are thrown or propelled in some way follow a trajectory in the shape of whats technically known as a parabola, which is basically a kind of curve. The word trajectory is commonly applied to the path of things that travel in this way, but it can be used more generally to simply refer to the route of something from one place to another, such as the trajectory of a storm. It can also be used in a more figurative way, as in careertrajectorymeaning the path that ones career has taken.
What Is The Use Of Trajectory Equation
The trajectory formula is used to find the trajectory or the flight path of a moving object which is moving under the action of gravity. The term trajectory is used for projectiles or heavenly objects. When a stone is thrown in the air, then the parabola is the correct approximation of the path of the projectile.
Don’t Miss: Holt Mcdougal Worksheets
Parabolic Motion Of Projectiles
Let us consider a ball projected at an angle with respect to the horizontal x-axis with the initial velocity u as shown below:
The point O is called the point of projection is the angle of projection and OB= Horizontal Range or Simply Range. The total time taken by the particle from reaching O to B is called the time of flight.
For finding different parameters related to projectile motion, we can make use of differential equations of motions:
How To Calculate Trajectories
Projectile motion refers to the motion of a particle that is imparted with an initial velocity but is subsequently subjected to no forces besides that of gravity.
This includes problems in which a particle is hurled at an angle between 0 and 90 degrees to the horizontal, with the horizontal usually being the ground. For convenience, these projectiles are assumed to travel in the plane, with x representing horizontal displacement and y vertical displacement.
The path taken by a projectile is referred to as its trajectory. The point of origin of the projectile in problems in which you need to calculate the trajectory is usually assumed to be for simplicity unless otherwise stated.
The trajectory of a projectile is a parabola if the particle is launched in such a way that is has a nonzero horizontal motion component, and there is no air resistance to affect the particle.
Recommended Reading: Homework 4 Angle Addition Postulate Answers
What Is The Difference Between Path And Trajectory
There is an important distinction between a path and a trajectory. A path is a spatial construct and tells us how we get from A to B through the world. A trajectory is a path plus a schedule. It tells us how quickly we should move along the path, at what time we should be at what point along the path.
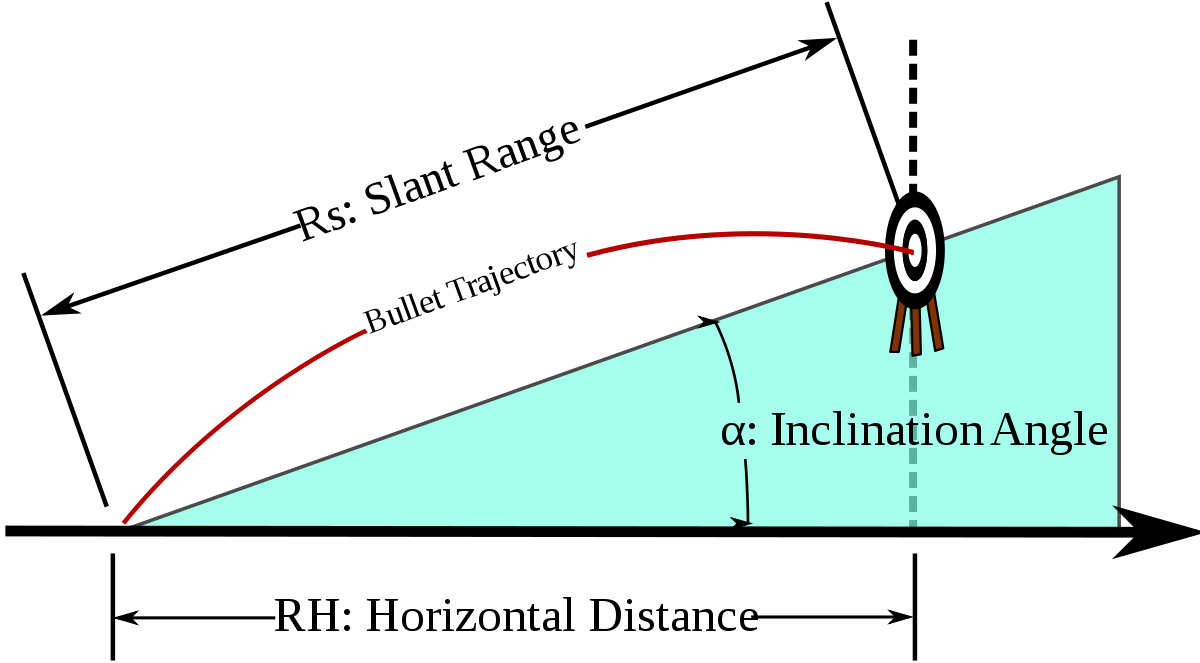
Uphill/downhill In Uniform Gravity In A Vacuum
Given a hill angle < math> \alpha< math> and launch angle < math> \theta< math> as before, it can be shown that the range along the hill < math> R_s< math> forms a ratio with the original range < math> R< math> along the imaginary horizontal, such that:
- < math> \frac =\sec \alpha < math>
In this equation, downhill occurs when < math> \alpha< math> is between 0 and -90 degrees. For this range of < math> \alpha< math> we know: < math> \tan=-\tan \alpha< math> and < math> \sec = \sec \alpha< math> . Thus for this range of < math> \alpha< math> ,< math> R_s/R=\sec \alpha < math> . Thus < math> R_s/R< math> is a positive value meaning the range downhill is always further than along level terrain. This makes perfect sense as it is expected that gravity will assist the projectile, giving it greater range.
While the same equation applies to projectiles fired uphill, the interpretation is more complex as sometimes the uphill range may be shorter or longer than the equivalent range along level terrain. Equation 11 may be set to < math> R_s/R=1< math> and solving for the “critical angle” < math> \theta_< math> :
- < math> 1=\sec \alpha \quad \ < math>
- < math> \theta_=\arctan\cot \alpha) \quad \ < math>
Equation 11 may also be used to develop the “rifleman’s rule” for small values of < math> \alpha< math> and < math> \theta< math> . For small values, both < math> \tan \alpha< math> and < math> \tan \theta< math> have a small value and thus when multiplied together , the result is almost zero. Thus equation 11 may be approximated as:
Recommended Reading: How To Learn Physics Fast
What Is Projectile Physics
A projectile is an object upon which the only force acting is gravity. A projectile is any object that once projected or dropped continues in motion by its own inertia and is influenced only by the downward force of gravity. By definition, a projectile has a single force that acts upon it the force of gravity.
Does Quantum Mechanics Imply That Particles Have No Trajectories
In Classical Mechanics we describe the evolution of a particle giving its trajectory. This is quite natural because it seems a particle must be somewhere and must have some state of motion. In Quantum Mechanics, on the other hand, we describe the evolution of a particle with its wave function $\Psi$ which is a function such that $|\Psi|^2$ is a probability density function for the position random variable.
In that case, solving the equations of the theory instead of giving the trajectory of the particle gives just statistical information about it. Up to there it is fine, these are just mathematical models. The model from Classical Mechanics has been confirmed with experiments in some situations and the Quantum Mechanics model has been confirmed with experiments in situations Classical Mechanics failed.
What is really troubling me is: does the fact that the Quantum Mechanics model has been so amply confirmed implies a particle has no trajectory? I know some people argue that a particle is really nowhere and that observation is what makes it take a stand. But, to be sincere, I don’t swallow that idea. It always seemed to me that it just reflects the fact that we don’t really know what is going on.
So, Quantum Mechanics implies that a particle has no trajectory whatsoever or particles do have well defined trajectories but the theory is unable to give any more information about then than just probabilities?
You say:
Here is an electron trajectory, the electron is a particle
Read Also: Geometry Dash Password Hack
Examples Of Projectile Motion
The key to being able to solve problems that include trajectory calculations is knowing that the horizontal and vertical components of motion can be analyzed separately, as shown above, and their respective contributions to overall motion neatly summed at the end of the problem.
Projectile motion problems count as free-fall problems because, no matter how things look right after time t = 0, the only force acting on the moving object is gravity.
- Be aware that because gravity acts downward, and this is taken to be the negative y-direction, the value of acceleration is -g in these equations and problems.
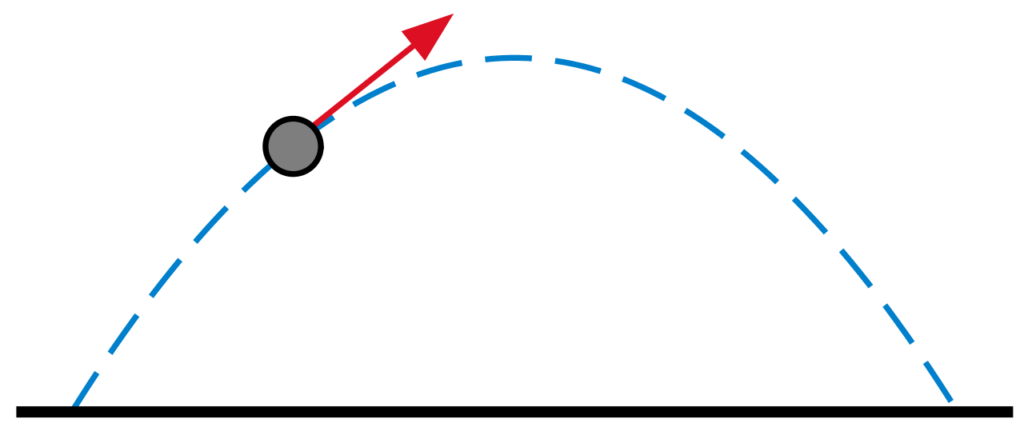
What Does Trajectory Mean In Physics
A trajectory or flight path is the path that an object with mass in motion follows through space as a function of time. In classical mechanics, a trajectory is defined by Hamiltonian mechanics via canonical coordinates hence, a complete trajectory is defined by position and momentum, simultaneously.
Recommended Reading: How To Find The Half Life
What Are The Key Components Of Projectile Motion
The key components that we need to remember in order to solve projectile motion problems are:
- Initial launch angle, \theta
- Initial velocity, \text
- Time of flight, \text
- Acceleration, \text
- Horizontal velocity, \text_\text
- Vertical velocity, \text_\text
- Displacement, \text
- Maximum height, \text
- Range, \text
How To Solve Any Projectile Motion Problem : Introducing the âToolboxâ method of solving projectile motion problems! Here we use kinematic equations and modify with initial conditions to generate a âtoolboxâ of equations with which to solve a classic three-part projectile motion problem.
Now, letâs look at two examples of problems involving projectile motion.
Aydanos A Mantenernos En Rbita
¿Nuestros contenidos te están resultando de utilidad?
Con un pequeño gesto podremos mantenernos en órbita. Regístrate para acceder a contenidos y funcionalidad exclusiva. Además, con tu ayuda podremos continuar ofreciendo nuestros servicios de manera gratuita para miles de estudiantes en todo el mundo. Te ofrecemos:
- Un campus virtual orientado a la gamificación
- Nuevos contenidos premium
The trajectory is the geometric line or path described by a moving body. In this section, we are going to study:
Read Also: Define Movement In Geography
How To Calculate The Trajectory Of A Projectile
Also, the trajectory has vertical and horizontal position components. Moreover, if we launch the projectile with an initial velocity , at an angle from the horizontal plane. Then we can find the vertical position of the object from the horizontal position using this formula
https://www.youtube.com/watch?v=megxZIDPXGI
What Is Projectile
A projectile is any object thrown into space upon which the only acting force is gravity. The primary force acting on a projectile is gravity. This doesnt necessarily mean that other forces do not act on it, just that their effect is minimal compared to gravity. The path followed by a projectile is known as a trajectory. A baseball batted or thrown is an example of the projectile.
Read Also: Beth Child Of Rage Now
Why Is S Position
S stands for the Latin word spatium, which means distance or space. In a Science Asylum video I learnt that s in displacement came from the German word strecke, which means route in English. This is possible, as German is often considered the second most important language in science and technology.
How Do You Use Trajectories In A Sentence
Trajectory in a Sentence ?
You May Like: Holt Geometry Chapter 7 Test Form A
Solved Examples On Trajectory Formula
Example 1
Firstly, suppose a cricket player hit a ball, guiding it away from the bat at a velocity of 45.0 m/s at an angle of \ in relation to the field. Moreover, if the direction of travel of the ball is towards the end of the field which is 140.0 m away. Then what will be the height of the ball when it will reach the end of the field?
Solution:
In this question the height of the ball is its vertical position and the horizontal position of attention in this question is end of the field which is x = 140.0 m. Also, we need to solve the vertical position y to know the height of the ball. Moreover, the angle \ and the initial velocity ) is present in the question. So, we can use the trajectory formula to solve for y.
y = x tan \ \
y = tan ) \^}cos^}\)
y \ – \^}^}\)
y \ – \}/s^)}\)
y \ 320.6 m- \
y \ 320.6 m- 296.4 m
y \ 24.2 m
So, the vertical position of the ball at the end of the field is y \ 24.2 m.
Example 2
Suppose a water skier plans to set up a stunt in which he is going to jump over a burning obstacle. Also, the fire will be 4.0 m away from the ramp, and it will be 1.0 m taller than the height of the ramp. Moreover, the ramp is inclined at an angle of \ in relation to the water. Furthermore, he plans to take off from the ramp at a velocity of 9.0 m/s. So, calculate if he will be able to jump over the flames or not?
Solution:
Horizontal position = 4.0 mVertical position = ?Initial velocity )\) = 9.0 m/sLunch angle = \
Putting values in the trajectory formula
What Is Trajectory Explain With Diagram
A trajectory or flight path is the path that an object with mass in motion follows through space as a function of time. In classical mechanics, a trajectory is defined by Hamiltonian mechanics via canonical coordinates hence, a complete trajectory is defined by position and momentum, simultaneously.
Recommended Reading: Mega Hack V5 Geometry Dash
What Does Mean Position Means
A mean position is any position that is a moderate position between two other extreme positions. It is understood as a middle-of-the-road position or compromise between two extreme views. In order for a position to be a mean position, it only needs to be more moderate than two identifiable extremes.
What Is An Example Of A Trajectory
The definition of a trajectory is the curved path something takes as it moves through space. An example of trajectory is the path taken by a paper airplane as it flies through the air. The curved path of something hurtling through space, esp. that of a projectile from the time it leaves the muzzle of the gun.
You May Like: Imaginary Numbers Worksheet Kuta
How Will You Describe The Trajectory Path Of The Ball
When a ball or any other object is projected through the air it will follow a curved trajectory until it hits the ground. The trajectory can be calculated easily if we ignore air resistance and assume that the only force acting on the ball is that due to gravity. The resulting ball path is then a parabola.
What Does Trajectory Mean
The trajectory of an object is the path it follows once in flight or in motion.
The word is especially used in the context of the path of projectiles like rockets, but it can be used in many different contexts.
The trajectory of a golf ball is the curved path it follows in the air after being hit by a golf club. The trajectory of an asteroid is the path it follows in space. The potential trajectory of a storm is the route that it may travel.
In geometry, trajectory is used in a more specific way to refer to a curve that intersects through a series of points at the same angle.
Example: Try to determine the trajectory of the ball as it flies through the air so you can position yourself to catch it.
Recommended Reading: Lewis Structure For Ccl4
What Is Projectile Motion
When a particle is thrown obliquely near the earths surface, it moves along a curved path under constant acceleration that is directed towards the centre of the earth . The path of such a particle is called a projectile and the motion is called projectile motion.
In a Projectile Motion, there are two simultaneous independent rectilinear motions:
Acceleration in the horizontal projectile motion and vertical projectile motion of a particle: When a particle is projected in the air with some speed, the only force acting on it during its time in the air is the acceleration due to gravity . This acceleration acts vertically downward. There is no acceleration in the horizontal direction, which means that the velocity of the particle in the horizontal direction remains constant.
Derivation Of The Trajectory Formula
y = refers to the vertical position of the object in metersx = refers to the horizontal position of the object in meters\ = refers to the initial velocity of the object combined with meter per secondg = refers to the acceleration due to gravity that is 9.80 \\ refers to the initial angle from the horizontal plane in degrees or radians.
You May Like: Define Consistent In Math
Properties Of Projectile Motion
Projectile motion is the motion of an object thrown into the air. After the initial force that launches the object, it only experiences the force of gravity. The object is called a projectile, and its path is called its trajectory. As an object travels through the air, it encounters a frictional force that slows its motion called air resistance. Air resistance does significantly alter trajectory motion, but due to the difficulty in calculation, it is ignored in introductory physics.