What Does Pythagorean Theorem Mean In Math

Math: How To Prove The Pythagorean Theorem

I hold both a bachelor’s and a master’s degree in applied mathematics.

This article will break down the history, definition, and use of the Pythagorean theorem.

The Pythagorean theorem is one of the most well-known theorems in math. It is named after the Greek philosopher and mathematician Pythagoras, who lived around 500 years before Christ. However, most probably he is not the one who actually discovered this relationship.

There are signs that already 2,000 B.C. the theorem was known in Babylonia. Also, there are references that show the use of the Pythagorean theorem in India around 800 B.C. In fact, it is not even clear whether Pythagoras had actually anything to do with the theorem, but because he had a big reputation the theorem was named after him.

The theorem as we know it now was first stated by Euclid in his book Elements as proposition 47. He also gave a proof, which was quite complicated. It definitely can be proven a lot easier.

Euclidean Distance In Other Coordinate Systems

If Cartesian coordinates are not used, for example, if polar coordinates are used in two dimensions or, in more general terms, if curvilinear coordinates are used, the formulas expressing the Euclidean distance are more complicated than the Pythagorean theorem, but can be derived from it. A typical example where the straight-line distance between two points is converted to curvilinear coordinates can be found in the applications of Legendre polynomials in physics. The formulas can be discovered by using Pythagoras’ theorem with the equations relating the curvilinear coordinates to Cartesian coordinates. For example, the polar coordinates can be introduced as:

x

, s^& =r_^+r_^-2r_r_\left\\& =r_^+r_^-2r_r_\cos \left\\& =r_^+r_^-2r_r_\cos \Delta \theta ,\end}}

using the trigonometric product-to-sum formulas. This formula is the law of cosines, sometimes called the generalized Pythagorean theorem. From this result, for the case where the radii to the two locations are at right angles, the enclosed angle = /2, and the form corresponding to Pythagoras’ theorem is regained: s

, ^\theta +^\theta =+b^}}}=1,}

What Does The Pythagorean Theorem Mean

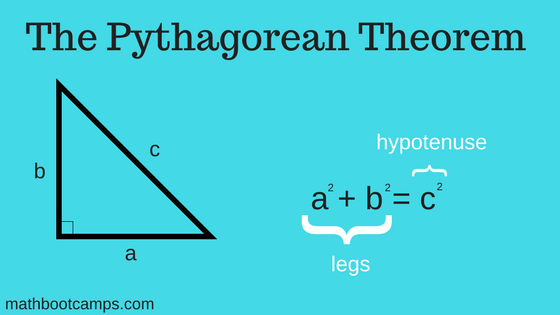
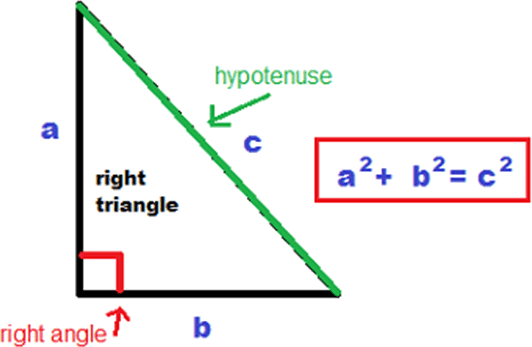
The Pythagorean Theorem is a mathematical formula that is used to find the missing side of a right angled triangle, and is given as:

#a^2 + b^2 = c^2#

which can be rearranged to give either: #b^2 = c^2-a^2# #a^2= c^2-b^2#

The side #c# is always the hypotenuse, or the longest side of the triangle, and the two remaining sides, #a# #b# can be interchanged as either the adjacent side of the triangle or the opposite side.

When finding the hypotenuse, the equation results in adding the sides, and when finding any other side, the equation results in the subtraction of the sides.

You May Like: Is Paris Jackson Michael’s Biological Daughter

What Is Pythagorean Theorem

We are already aware of the definition and properties of a right-angled triangle. In this triangle with one of its angles as a right angle, it means 90 degrees. The side which is opposite to the 90-degree angle is termed as the hypotenuse. The other two sides which are adjacent to the right angle are called legs of the triangle.

The Pythagorean Theorem is a very useful formula for determining the length of a side of a right triangle. This formula has many direct and indirect applications in the geometrical derivations and applications. In the triangle, the hypotenuse is the longest side.

We may easily locate the longest side by looking across from the right angle. The other two legs will be base and perpendicular, which are making a 90-degree angle. There is no specific rule to consider the side as base or perpendicular. It does not matter at all.

The Pythagoras theorem is also termed as the Pythagorean Theorem. This theorem states that the square of the length of the hypotenuse will be equal to the sum of the squares of the lengths of the other two sides of the right-angled triangle. In other words, the sum of the squares of the two legs of a right triangle will be equal to the square of its hypotenuse.

Proofs By Dissection And Rearrangement

Another by rearrangement is given by the middle animation. A large square is formed with area c2, from four identical right triangles with sides a, b and c, fitted around a small central square. Then two rectangles are formed with sides a and b by moving the triangles. Combining the smaller square with these rectangles produces two squares of areas a2 and b2, which must have the same area as the initial large square.

The third, rightmost image also gives a proof. The upper two squares are divided as shown by the blue and green shading, into pieces that when rearranged can be made to fit in the lower square on the hypotenuse or conversely the large square can be divided as shown into pieces that fill the other two. This way of cutting one figure into pieces and rearranging them to get another figure is called dissection. This shows the area of the large square equals that of the two smaller ones.

Also Check: What Does Kw Mean In Chemistry

Faqs On Pythagoras Theorem

Question 1: What is the Converse of Pythagoras Theorem?

Answer:

The converse of Pythagoras theorem states that if the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.

Question 2: What are the applications of Pythagoras Theorem?

Answer:

• In order to calculate the surface area and volume, etc.

Question 3: What is Pythagoras theorem in math?

Answer:

The Pythagoras theorem provides us with the relationship between the sides in a right-angled triangle. The square of the hypotenuse is equal to the sum of the sides of the perpendicular and base. It can be written as:

c2 = a2 + b2

Where c is the hypotenuse, a and b are the legs of the right-angled triangle.

Question 4: Where can the Pythagoras theorem be applied?

Answer:

It is important to note that Pythagoras theorem can not be applied to any triangle. Pythagoras theorem is not applicable for the triangles that are not right-angled.

arrow_drop_up

How To Do The Pythagorean Theorem

Consider a right triangle above.

Given that:

Let BD be the perpendicular line to the side AC.

Similar s:

ADB and ABC are similar triangles.

From the similarity rule,

AD × AC = 2

Similarly

BDC and ABC are similar triangles. Therefore

DC/BC = BC/AC

DC × AC = 2

× AC = 2 + 2

2 = 2 + 2

Therefore, if we let AC = c AB = b and BC = b, then

c2 = a2 + b2

There are many demonstrations of the Pythagorean Theorem given by different mathematicians.

Another common demonstration is to draw the 3 squares in such a way that they form a right triangle in between, and the area of the bigger square is equal to the sum of the area of the smaller two squares .

Consider the 3 squares below:

They are drawn in such a way that they form a right triangle. We can write their areas can in equation form:

Area of Square III= Area of Square I + Area of Square II

Lets suppose the length of square I, square II, and square III are a, b and c, respectively.

Then,

Area of Square I = a 2

Area of Square II = b 2

Area of Square III = c 2

Hence, we can write it as:

a 2 + b 2 = c 2

which is a Pythagorean Theorem.

Read Also: Why Do People Copy Others Psychology

Proof Of Pythagorean Theorem Formula Using The Algebraic Method

The proof of the Pythagoras theorem can be derived using the algebraic method. For example, let us use the values a, b, and c as shown in the following figure and follow the steps given below:

• Step 1: Arrange four congruent right triangles in the given square PQRS, whose side is a + b. The four right triangles have ‘b’ as the base, ‘a’ as the height and, ‘c’ as the hypotenuse.
• Step 2: The 4 triangles form the inner square WXYZ as shown, with ‘c’ as the four sides.
• Step 3: The area of the square WXYZ by arranging the four triangles is c2.
• Step 4: The area of the square PQRS with side = Area of 4 triangles + Area of the square WXYZ with side ‘c’. This means 2 = + c2.This leads to a2 + b2 + 2ab = 2ab + c2. Therefore, a2 + b2 = c2. Hence proved.

What Is The Pythagoras Theorem

The Pythagoras theorem states that if a triangle is right-angled , then the square of the hypotenuse is equal to the sum of the squares of the other two sides. Observe the following triangle ABC,in whichwe have BC2 = AB2 + AC2. Here, AB is the base, AC is the altitude , and BC is the hypotenuse. It is to be noted that the hypotenuse is the longest side of a right-angled triangle.

Don’t Miss: What Is Learning Theory In Psychology

Applications Of Pythagoras Theorem

The applications of the Pythagoras theorem can be seen in our day-to-day life. Here are some of the applications of the Pythagoras theorem.

• Engineering and Construction fields

Most architects use the technique of the Pythagorean theorem to find the unknown dimensions. When length or breadth are known it is very easy to calculate the diameter of a particular sector. It is mainly used in two dimensions in engineering fields.

• Face recognition in security cameras

The face recognition feature in security cameras uses the concept of the Pythagorean theorem, that is, the distance between the security camera and the location of the person is noted and well-projected through the lens using the concept.

• Woodwork and interior designing

The Pythagoras Theorem Formula

The Pythagoras Theorem formula is given as:

c2 = a2 + b2

c = Length of the hypotenuse

a = length of one side

b = length of the second side.

We can use this formula to solve various problems involving right-angled triangles. For instance, we can use the formula to determine the third length of a triangle when the lengths of two sides of the triangle are known.

Also Check: Geometry Dash Demon Key Hack

Application Of Pythagoras Theorem Formula In Real Life

• We can use the Pythagoras theorem to check whether a triangle is a right triangle or not.
• In oceanography, the formula is used to calculate the speed of sound waves in water.
• Pythagoras theorem is used in meteorology and aerospace to determine the sound source and its range.
• We can use the Pythagoras theorem to calculate electronic components such as tv screens, computer screens, solar panels, etc.
• We can use the Pythagorean Theorem to calculate the gradient of a certain landscape.
• In navigation, the theorem is used to calculate the shortest distance between given points.
• In architecture and construction, we can use the Pythagorean theorem to calculate the slope of a roof, drainage system, dam, etc.

Worked examples of Pythagoras theorem:

Example 4

The two short sides of a right triangle are 5 cm and 12cm. Find the length of the third side

Solution

How Is The Pythagorean Theorem Useful Today

The Pythagorean theorem isn’t just an intriguing mathematical exercise. It’s utilized in a wide range of fields, from construction and manufacturing to navigation.

As Allen explains, one of the classic uses of the Pythagorean theorem is in laying the foundations of buildings. “You see, to make a rectangular foundation for, say, a temple, you need to make right angles. But how can you do that? By eyeballing it? This wouldn’t work for a large structure. But, when you have the length and width, you can use the Pythagorean theorem to make a precise right angle to any precision.”

Beyond that, “This theorem and those related to it have given us our entire system of measurement,” Allen says. “It allows pilots to navigate in windy skies, and ships to set their course. All GPS measurements are possible because of this theorem.”

In navigation, the Pythagorean theorem provides a ship’s navigator with a way of calculating the distance to a point in the ocean that’s, say, 300 miles north and 400 miles west . It’s also useful to cartographers, who use it to calculate the steepness of hills and mountains.

“This theorem is important in all of geometry, including solid geometry,” Allen continues. “It is also foundational in other branches of mathematics, much of physics, geology, all of mechanical and aeronautical engineering. Carpenters use it and so do machinists. When you have angles, and you need measurements, you need this theorem.”

Also Check: What Is N In Physics

Pythagorean Theorem Explanation & Examples

The Pythagorean Theorem, also referred to as the Pythagoras theorem, is arguably the most famous formula in mathematics that defines the relationships between the sides of a right triangle.

The theorem is attributed to a Greek mathematician and philosopher named Pythagoras . He has many contributions to mathematics, but the Pythagorean Theorem is the most important of them.

Pythagoras is in mathematics, astronomy, music, religion, philosophy, etc. One of his notable contributions to mathematics is the discovery of the Pythagorean Theorem. Pythagoras studied the sides of a right triangle and discovered that the sum of the square of the two shorter sides of the triangles is equal to the square of the longest side.

This article will discuss what the Pythagorean Theorem is, its converse, and the Pythagorean Theorem formula. Before getting deeper into the topic, lets recall the right triangle. A right triangle is a triangle with one interior angle equals 90 degrees. In a right triangle, the two short legs meet at an angle of 90 degrees. The hypotenuse of a triangle is opposite the 90-degree angle.

And You Can Prove The Theorem Yourself

Get paper pen and scissors, then using the following animation as a guide:

• Draw a right angled triangle on the paper, leaving plenty of space.
• Draw a square along the hypotenuse
• Draw the same sized square on the other side of the hypotenuse
• Draw lines as shown on the animation, like this:
• Cut out the shapes
• Arrange them so that you can prove that the big square has the same area as the two squares on the other sides

Don’t Miss: What Is Av Shaped Valley In Geography

How To Work Out Pythagoras Theorem

Pythagoras theorem can be used to find the unknown side of a right-angled triangle. For example, if two legs of a right-angled triangle are given as 4 units and 6 units, then the hypotenuse can be calculated using the formula, c2 = a2 + b2 where ‘c’ is the hypotenuse and ‘a’ and ‘b’ are the two legs. Substituting the values in the formula, c2 = a2 + b2 = c2 = 42 + 62 = 16 + 36 = 52 = 7.2 units.

How To Find Whether A Triangle Is A Right

If we are provided with the length of three sides of a triangle, then to find whether the triangle is a right-angled triangle or not, we need to use the Pythagorean theorem.

Let us understand this statement with the help of an example.

Suppose a triangle with sides 10cm, 24cm, and 26cm are given.

Clearly, 26 is the longest side.

It also satisfies the condition, 10 + 24 > 26

We know,

So, let a = 10, b = 24 and c = 26

First we will solve R.H.S. of equation 1.

a2 + b2 = 102 + 242 = 100 + 576 = 676

Now, taking L.H.S, we get

c2 = 262 = 676

ac = 42.

Thus, the length of the diagonal is 42 cm.

Stay tuned with BYJUS The Learning App to learn all the important mathematical concepts and also watch interactive videos to learn with ease.

Recommended Reading: What Is 1 Mole In Chemistry

Both Areas Must Be Equal

The area of the large square is equal to the area of the tilted square and the 4 triangles. This can be written as:

= c2 + 2ab

NOW, let us rearrange this to see if we can get the pythagoras theorem:

DONE!

Now we can see why the Pythagorean Theorem works … and it is actually a proof of the Pythagorean Theorem.

This proof came from China over 2000 years ago!

There are many more proofs of the Pythagorean theorem, but this one works nicely.

Another Amazingly Simple Proof

Here is one of the oldest proofs that the square on the long side has the same area as the other squares.

Watch the animation, and pay attention when the triangles start sliding around.

You may want to watch the animation a few times to understand what is happening.

The purple triangle is the important one.

Recommended Reading: What Is The Meaning Of Remainder In Math

Converse Of Pythagoras Theorem

The converse of the Pythagoras theorem is very similar to Pythagoras theorem. To understand this theorem, you should think from the reverse of Pythagoras theorem.

If the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.

General Triangles Using Parallelograms

Pappus’s area theorem is a further generalization, that applies to triangles that are not right triangles, using parallelograms on the three sides in place of squares . The upper figure shows that for a scalene triangle, the area of the parallelogram on the longest side is the sum of the areas of the parallelograms on the other two sides, provided the parallelogram on the long side is constructed as indicated . This replacement of squares with parallelograms bears a clear resemblance to the original Pythagoras’ theorem, and was considered a generalization by Pappus of Alexandria in 4 AD

The lower figure shows the elements of the proof. Focus on the left side of the figure. The left green parallelogram has the same area as the left, blue portion of the bottom parallelogram because both have the same base b and height h. However, the left green parallelogram also has the same area as the left green parallelogram of the upper figure, because they have the same base and the same height normal to that side of the triangle. Repeating the argument for the right side of the figure, the bottom parallelogram has the same area as the sum of the two green parallelograms.

Recommended Reading: How Did Russia’s Geography Affect Its Early History