What Is The Meaning Of Remainder In Math

How To Get A Remainder In Your Calculator

When you work out a long division problem on your calculator, by default, it gives you the result as a whole number followed by a decimal with numbers after the decimal. But depending on the context for the division problem, you might require the answer as a whole number with a remainder instead. While most scientific calculators have a remainder function that you can locate either on the keyboard or by scrolling through their menus, this quick trick lets you calculate remainders with any calculator at all.

TL DR

Work the division in your calculator as normal. Once you have the answer in decimal form, subtract the whole number, then multiply the decimal value that’s left by the divisor of your original problem. The result is your remainder.

For example, divide 346 by 7 to arrive at 49.428571. Round this to a whole number of 49. Multiply 49 by 7 to achieve 343 expressed as 49 × 7 = 343. Subtract this from the original number of 346 to arrive at a remainder of 3.

Finding Remainders Using Long Division

We cannot always pictorially show how we divide the number of things equally among the groups in order to find the remainder. Instead, we can find the remainder using the long division method. For example, the remainder in the above example on cookies can be found using long division as follows:

Thus, the remainder is 3. A remainder can also be a 0. The remainder on dividing 10 by 2, 18 by 3, or 35 by 7, is equal to 0. Here are some other examples of remainders.

You can check these remainders by long division.

How To Represent Remainder

Let us divide 7 by 2 using long division and see what the quotient and the remainder are. The quotient, divisor, the remainder can be together written as a mixed fraction to represent the dividend. The remainder forms the numerator of the mixed fraction, the divisor forms the denominator, and the quotient form the whole number part of the mixed fraction.

We can represent the remainder of the division in two ways.

• One is by writing the quotient and the remainder with an “R” in between them. The number 7 divided by 2 can be written as 7/2 = Q=3 and R=1. Here Q=3 is a quotient and R=1 is a remainder.
• Another way to represent the remainder is by showing it as a part of a mixed fraction. The number 7 divided by two can be written as 7/2 = 3½

Read Also: How To Do Elimination In Math

How To Estimate The Quotient

Check out the step-by-step process to calculate the estimating quotient of two numbers.

• If the numbers have two or more digits, then round off the numbers to the nearest 10 or 100 or 1000.
• And divide those numbers to get the quotient.
• The obtained quotient is called the estimated quotient of the given numbers.

Also, Read More Articles:

Round off the divided and divisor to the nearest 10

new divided = 80, new divisor = 40

80 ÷ 40 = 2

Estimated quotient = 2.

Example 2:

A school track is 9.76 meters wide. It is divided into 8 lanes of equal width. How wide is each lane?

Solution:

The width of each lane is nothing but the quotient when we divide 9.76 by 8.

Round off the school track to the nearest 10 i.e 9.76 is 10.

Divide 10 by 8

Approximately, 1 meter wide each lane.

Example 3:

Aerobics classes cost $153.86 for 14 sessions. What is the estimated fee for one session?

Solution:

The fee for one session is nothing but the quotient when we divide 153.86 by 14.

Round off 153.86 to the nearest 10 i.e 150

Round off 14 to the nearest 10 i.e 10

Divide 150 by 10

Therefore, the estimated fee for one session is $15.

Example 4:

Estimate quotient when 1058 divided by 50.

Solution:

Round off 1058 to the nearest 100 i.e 1100

Divide 1100 by 50

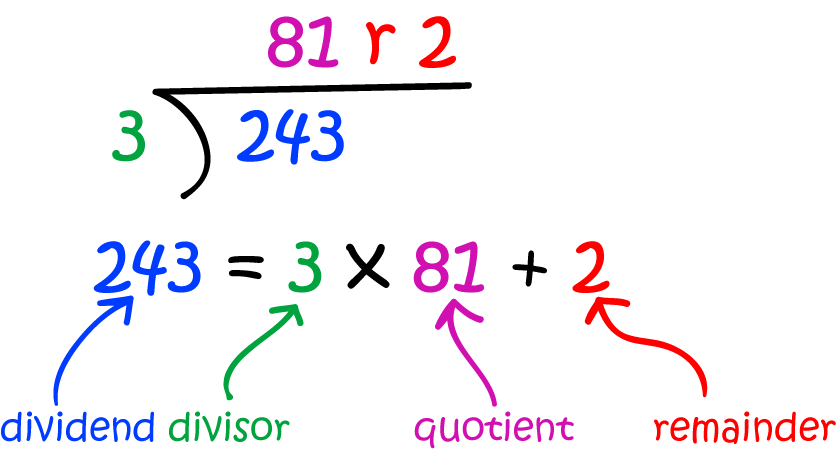
Dividend Divisor Quotient And Remainder

When you perform division, you can typically write down this operation in the following way:

• a Initial number you want to divide, called the dividend
• n Number you divide by it is called the divisor
• q Result of division rounded down to the nearest integer it is called the quotient and
• rRemainder of this mathematical operation.

When performing division with our calculator with remainders, it is important to remember that all of these values must be integers. Otherwise, the result will be correct in the terms of formulas, but will not make mathematical sense.

Make sure to check our modulo calculator for a practical application of the calculator with remainders.

Also Check: Holt Geometry Chapter 7 Test Answer Key

Setting Up The Problem

Before you figure out a division problem with a calculator, it helps to have some basic terms straight. The number divided into is the dividend, the number you’re dividing it by is the divisor and the answer is the quotient. Often, you’ll see division problems written like this: Dividend ÷ divisor = quotient. If you were to write your division problem out as a fraction, the number on top is the dividend, and the number on bottom is the divisor.

Find the remainder of a division problem with your calculator, by working the division as usual. You’ll get a decimal answer that’s fine.

Subtract the integer from the answer you received. You’re left with only the part of the answer that was to the right of the decimal point.

Multiply what’s left of your answer by the initial divisor. The result is your remainder. For example, if the initial problem was 11 ÷ 8, the calculator returns an answer of 1.375. After subtracting the integer, 1, youre left with .375. Multiply that by 8 and you have the remainder: 3.

Tips

• Remember, the divisor is the number to the right of the ÷ sign or, if you wrote the division problem out as a fraction, it’s the number on the bottom of the fraction. If you’re writing out long division, the divisor is the number to the left of the long division sign.

Related Articles

What Is The Remainder When 599 Is Divided By 9

The remainder is 5. To calculate this, first, divide 599 by 9 to get the largest multiple of 9 before 599. 5/9 < 1, so carry the 5 to the tens, 59/9 = 6 r 5, so carry the 5 to the digits. 59/9 = 6 r 5 again, so the largest multiple is 66. Multiply 66 by 9 to get 594, and subtract this from 599 to get 5, the remainder.

Don’t Miss: Eoc Fsa Warm Ups Algebra 1 Answers

What Is The Remainder Theorem

Polynomials of degree 3 or higher are difficult to factorize, so long division or synthetic division techniques are used to solve this problem. These methods are quite popular and frequently used by students during their early school studies. However, students are always in the need of a shortcut. This is where the concept of remainder theorem came into existence.

Once you will complete this article, you will get to know how you can use the remainder theorem to factorize the polynomial and what are the applications in the real-life. This is true that remainder theorem does not give you much information like other theorems, still an effective style to continue with the factorization.

Before we continue ahead, let us consider a simple example of listing factors of 27. If you would look closely, probably the factors are 1,3,9, and 27 and the remainder is zero. The method is simpler in case of an integer but what is the solution if you are using the polynomials. Other than these, if you are going to divide 27 with any other number then it will leave a remainder. For example, if you will divide the 27 with 6 then it will give a remainder of 3.

Estimating The Quotient Definition Examples

The division is a basic arithmetic operation and it is the inverse of multiplication. The terms of division are dividend, divisor, quotient, and remainder. The number which we divide is known as a dividend, the number by which we divide is called the divisor. The quotient means the number of times a division is completed fully, and the remainder is the quantity that doesnt go fully into the divisor. Here, we will learn about how to estimate the quotient of two numbers easily with solved example questions.

Don’t Miss: The Segment Addition Postulate Answer Key With Work

How Do You Solve Chinese Remainder Theorem Problems

Princeton’s Wordnetrate This Definition:

Don’t Miss: What Math Class Do 11th Graders Take

Implementing Other Modulo Definitions Using Truncation

Despite the mathematical elegance of Knuth’s floored division and Euclidean division, it is generally much more common to find a truncated division-based modulo in programming languages. Leijen provides the following algorithms for calculating the two divisions given a truncated integer division:

/* Euclidean and Floored divmod, in the style of C's ldiv */typedefstructldiv_t /* Euclidean division */inlineldiv_tldivEelse}return }/* Floored division */inlineldiv_tldivFreturn }

Note that for both cases, the remainder can be calculated independently of the quotient, but not vice versa. The operations are combined here to save screen space, as the logical branches are the same.

What Is Estimating The Quotient

When we divide two numbers, the result we get is called the quotient. The formula to express the terms of division is divided ÷ divisor = quotient + remainder. It is important to know how to estimate the quotient. Estimating the quotient means, we not doing the division for the actual numbers. You need to round off the dividend and divisor to the nearest 10 and proceed for the division to get the estimated quotient value.

Don’t Miss: Geometry Segment Addition Postulate Worksheet

Examples On Remainder In Division

How To Find The Remainder In Division

The steps to long division with a remainder are easy to recall using the mnemonic : Does McDonalds Sell Cheese Burgers Daily?:

• Does = Divide
• McDonalds = Multiply
• Sell = Subtract
• Cheese = Compare
• Burgers Daily = Bring Down

If a difference remains after completing all five steps with all the digits of the dividend, that difference is the remainder.

Also Check: Eoc Fsa Warm Ups Algebra 1 Answers

Dividend Divisor Quotient Remainder

These Math terms relate to division. See the graphics below.

Dividend is the number to be divided.

Divisor is the number divided into or the number of groups.

Quotient is the answer you get after dividing. You can think of it as the number inside each group.

Remainder is the number left over. The remainder must always be smaller than the divisor.

If the remainder is bigger than the divisor it means the quotient is too small.

Ring Of Remainders Definition

My notes on Euclidean domains state a notion of ring of remainders that I should connect with the quotient by certain ideal but I don’t see quite how the connection is done.

Given an euclidean domain $D$ with unique quotient and remainder defined and $m \in D \setminus \$, we define the ring of remainders $D_m$ as the set $\$ together with operations $a+b = R_m$ and $ab = R_m$.

Where $R_m$ is the function that gives the unique euclidean remainder of the division by $m$. This is done having in mind $K,\mathbb_n$. Then, the notes continue stating that $R_m:D \to D_m$ is an homomorphism and therefore $D/mD \cong D_m$.

However, I’m missing properties for $R_m$ to be a ring homomorphism. For instance, $R_m$ does not need to be $1$ as in $\mathbb$, $ = 1$ and $R_m = 0$ .

Have you encountered anything similar to this before? The only similar text I can find is this.

Don’t Miss: What Does G Stand For In Physics

Variants Of The Definition

In mathematics, the result of the modulo operation is an equivalence class, and any member of the class may be chosen as representative however, the usual representative is the least positive residue, the smallest non-negative integer that belongs to that class . However, other conventions are possible. Computers and calculators have various ways of storing and representing numbers thus their definition of the modulo operation depends on the programming language or the underlying hardware.

In nearly all computing systems, the quotient q and the remainder r of a divided by n satisfy the following conditions:

However, this still leaves a sign ambiguity if the remainder is non-zero: two possible choices for the remainder occur, one negative and the other positive, and two possible choices for the quotient occur. In number theory, the positive remainder is always chosen, but in computing, programming languages choose depending on the language and the signs of a or n. Standard Pascal and ALGOL 68, for example, give a positive remainder even for negative divisors, and some programming languages, such as C90, leave it to the implementation when either of n or a is negative . a modulo 0 is undefined in most systems, although some do define it as a.

As described by Leijen,

However, truncated division satisfies the identity (

Different Ways Of Representation Of Divisor

There are different styles of expressing a division equation. In the images below, the various methods of writing a divisor are shown below:

1. The number 1 is the divisor of all the numbers.

Reason: When the divisor is 1, then the quotient is the same as the dividend.

Look at the given examples,

34 1 = 34

15 1 = 15

2. The number itself is always one of the divisors of the number.

Reason: When the divisor is the same as the dividend, then the answer to such a division is always 1.

Look at the given examples,

34 34 = 1

15 15 = 1

3. When the divisor is a smaller number than the dividend, then the answer is not a whole number but a decimal number.

For example,

Recommended Reading: Ccl4 Dot Structure

S To Divide A Polynomial By A Non

• First, arrange the polynomials in the decreasing order of its degree
• Divide the first term of the dividend by the first term of the divisor to produce the first term of the quotient
• Multiply the divisor by the first term of the quotient and subtract this product from the dividend, to get the remainder.
• This remainder is the dividend now and divisor will remain same
• Again repeat from the first step, until the degree of the new dividend is less than the degree of the divisor.

What Is Remainder In Division

The remainder, as its name suggests, is something that “remains” after completing a task. In math, the number 17 cannot be exactly divided by the number 3. After division, the number 2 is left aside as a reminder. As an example, let us assume that you have 15 cookies that you want to share with 3 of your friends, Mary, David, and Jake. You want to share the cookies equally among your friends and yourself. You will be distributing them in the following way.

Here, you can see that there are 3 cookies “remaining” after the distribution. These 3 cookies cannot be further shared equally among the 4 of you. Hence, 3 is called the “remainder”. Also, on observation, the remaining 3 cookies are less in number than the 4 people, with whom the cookies have been shared. We can understand that the remainder is always lesser than the divisor.

Recommended Reading: Chapter Test B Geometry Answers