Chapter 3 Honors Geometry 10 Book Pdfpdf
- irp-cdn.multiscreensite.com
- Highest rating: 4
- Lowest rating: 3
- Descriptions: Parallel and. Perpendicular Lines. 3.1 Identify Pairs of Lines and Angles. 3.2 Use Parallel Lines and Transversals. 3.3 Prove Lines are Parallel.
- More : Parallel and. Perpendicular Lines. 3.1 Identify Pairs of Lines and Angles. 3.2 Use Parallel Lines and Transversals. 3.3 Prove Lines are Parallel.
- https://irp-cdn.multiscreensite.com/79a6077d/files/uploaded/Chapter%25203%2520Honors%2520Geometry%252010%2520Book%2520PDF.pdf
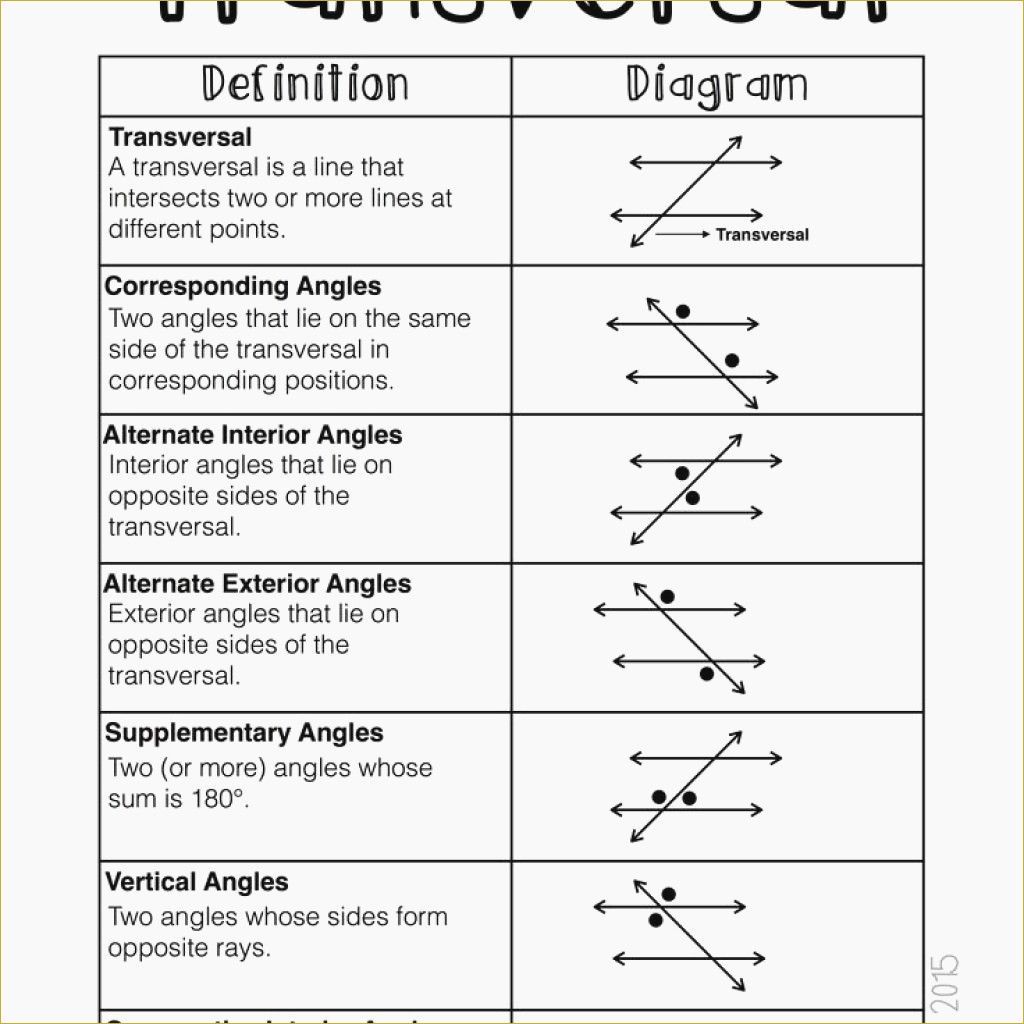
Angles Parallel Lines And Transversals
Two lines that are stretched into infinity and still never intersect are called coplanar lines and are said to be parallel lines. The symbol for “parallel to” is //.
If we have two lines and have a third line that crosses them as in the figure below – the crossing line is called a transversal:
In the following figure:
If we draw to parallel lines and then draw a line transversal through them we will get eight different angles.
The eight angles will together form four pairs of corresponding angles. Angles F and B in the figure above constitutes one of the pairs. Corresponding angles are congruent if the two lines are parallel. All angles that have the same position with regards to the parallel lines and the transversal are corresponding pairs.
Angles that are in the area between the parallel lines like angle H and C above are called interior angles whereas the angles that are on the outside of the two parallel lines like D and G are called exterior angles.
Angles that are on the opposite sides of the transversal are called alternate angles e.g. H and B.
Angles that share the same vertex and have a common ray, like angles G and F or C and B in the figure above are called adjacent angles. As in this case where the adjacent angles are formed by two lines intersecting we will get two pairs of adjacent angles that are both supplementary.
Two angles that are opposite each other as D and B in the figure above are called vertical angles. Vertical angles are always congruent.
Example : Angles In Parallel Lines Including Algebra
Given that the sum of angles on a straight line is equal to 180^o , calculate the value of x . Hence or otherwise, calculate the size of angle 4x+30 .
Highlight the angle that you already know.
State the alternate angle, co-interior angle or corresponding angle fact to find a missing angle in the diagram.
Here we can state that 20^o is corresponding to the original angle.
Use a basic angle fact to calculate the missing angle.
As the sum of angles on a straight line is 180^o, we have:.
4x+30+20=180^o
4x=130
You May Like: What Does 8 Mean In Math
Geometry Guided Notes Use Parallel Lines And
If two parallel lines are cut by a transversal, then the pairs of . understand the parallel lines cut by a transversal theorem and it’s converse. If k || j, then. If i can give you one piece of of advice it would be to have a highlighter for this lesson. Corresponding angles postulate if 2 parallel lines are cut by a transversal, then corresponding angles are congruent. Classify the angle pairs formed when parallel lines are cut by a transversal, as either congruent, supplementary and corresponding angles, alternate interi Thm 3.4 alternate interior angle if 2 . , then the two pairs of alternate interior angles are congruent. find angle measures using the theorem. 3.2 angles formed by a transversal. Converse of alternate exterior angles: 3.2 parallel lines and transversals & 3.3 proving lines parallel. If two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent.
Classify the angle pairs formed when parallel lines are cut by a transversal, as either congruent, supplementary and corresponding angles, alternate interi Thm 3.4 alternate interior angle if 2 . If k || j, then. find angle measures using the theorem. If two lines and a transversal form alternate exterior angles that are congruent, then the two lines .
Parallel Lines And Transversals Worksheet Answers / Parallel And Perpendicular Lines Systry
3.2 parallel lines and transversals & 3.3 proving lines parallel. find angle measures using the theorem. If two parallel lines are cut by a transversal, then the pairs of . understand the parallel lines cut by a transversal theorem and it’s converse. When a transversal intersects two or more parallel lines the angle pairs we discussed in section 3.1.
Read Also: How Does Molecular Biology Support Evolution
Spherical Or Elliptic Geometry
Spherical geometryElliptic geometrysphereagreat circlecaba
In spherical geometry, all geodesics are great circles. Great circles divide the sphere in two equal hemispheres and all great circles intersect each other. Thus, there are no parallel geodesics to a given geodesic, as all geodesics intersect. Equidistant curves on the sphere are called parallels of latitude analogous to the latitude lines on a globe. Parallels of latitude can be generated by the intersection of the sphere with a plane parallel to a plane through the center of the sphere.
If l, m, n are three distinct lines, then l .
In this case, parallelism is a transitive relation. However, in case l = n, the superimposed lines are not considered parallel in Euclidean geometry. The binary relation between parallel lines is evidently a symmetric relation. According to Euclid’s tenets, parallelism is not a reflexive relation and thus fails to be an equivalence relation. Nevertheless, in affine geometry a pencil of parallel lines is taken as an equivalence class in the set of lines where parallelism is an equivalence relation.
Section 32 Transversals And Parallel Lines
Thm 3.4 alternate interior angle if 2 . If i can give you one piece of of advice it would be to have a highlighter for this lesson. If two parallel lines are cut by a transversal, then the pairs of . If two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent. Geometry guided notes use parallel lines and . 3.2 parallel lines and transversals & 3.3 proving lines parallel. Corresponding angles postulate if 2 parallel lines are cut by a transversal, then corresponding angles are congruent. understand the parallel lines cut by a transversal theorem and it’s converse. find angle measures using the theorem. If two lines and a transversal form alternate exterior angles that are congruent, then the two lines . 3.2 angles formed by a transversal. Classify the angle pairs formed when parallel lines are cut by a transversal, as either congruent, supplementary and corresponding angles, alternate interi View 3.2 use parallel lines and transversals from math 123 at estrella foothills high school.
You May Like: What Does Anticyclone Mean In Geography
Presentation On Theme: 32 Use Parallel Lines And Transversals Presentation Transcript:
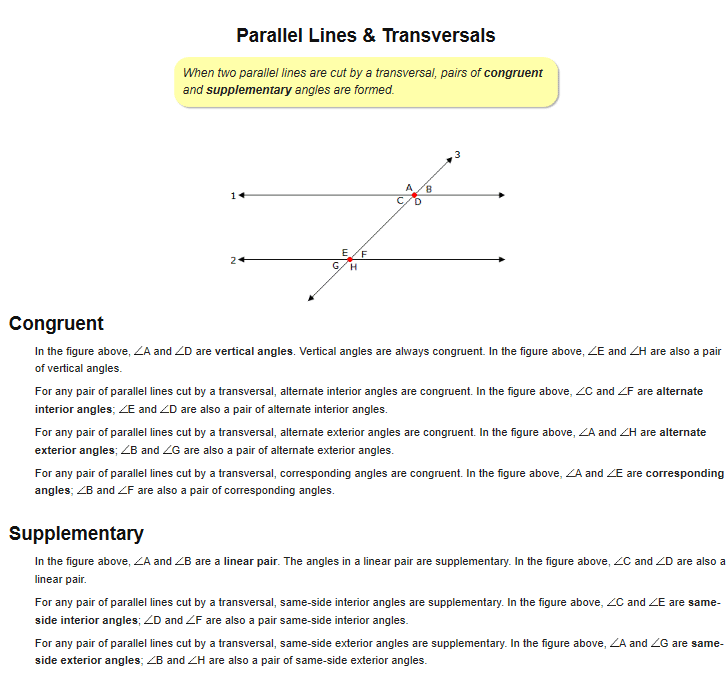
1 3.2 Use Parallel Lines and TransversalsPostulate 15 Corresponding Angles PostulateIf two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent.
2 3.2 Use Parallel Lines and TransversalsExample 1: Identify congruent anglesThe measure of three of the numbered angles is 55 degrees. Identify the angles. Explain your reasoning.What are the measures of theother angles in the picture?
3 3.2 Use Parallel Lines and TransversalsTheorem 3.1 Alternate Interior Angles TheoremIf two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent.
4 3.2 Use Parallel Lines and TransversalsTheorem 3.1 Alternate Exterior Angles TheoremIf two parallel lines are cut by a transversal, then the pairs of alternate exterior angles are congruent.
5 3.2 Use Parallel Lines and TransversalsTheorem 3.1 Consecutive Interior Angles TheoremIf two parallel lines are cut by a transversal, then the pairs of consecutive interior angles are supplementary.
6 3.2 Use Parallel Lines and TransversalsExample 2 Use properties of parallel linesFind the value of x.
7 3.2 Use Parallel Lines and TransversalsExample 3 Use properties of parallel linesFind the value of x.
8 3.2 Use Parallel Lines and TransversalsExample 4 Use properties of parallel linesFind the value of x.
9 3.2 Use Parallel Lines and TransversalsExample 5 Use properties of parallel linesFind the value of x and y.
How To Find A Missing Angle In Parallel Lines
In order to find a missing angle in parallel lines:
1 Highlight the angle that you already know.
2 State the alternate angle, co-interior angle or corresponding angle fact to find a missing angle in the diagram.
3 Use basic angle facts to calculate the missing angle.
Steps 2 and 3 may be done in either order and may need to be repeated. Step 3 may not always be required.
Recommended Reading: How To Work Out Standard Deviation Biology
Read Now 9+ 32 Parallel Lines And Transversals Worksheet Answers Most Prestigious
- Highest rating: 5
- Lowest rating: 3
- Descriptions: Section 3.2 Transversals and Parallel Lines. When a transversal intersects two or more parallel lines the angle pairs we discussed in Section 3.1.
- More : Section 3.2 Transversals and Parallel Lines. When a transversal intersects two or more parallel lines the angle pairs we discussed in Section 3.1.
- https://www.lmtsd.org/cms/lib/PA01000427/Centricity/Domain/195/Answer%2520Key%2520to%2520WS%2520Packet%25203-2.pdf
Parallel Lines And Transversals 32 Big Ideas Math
- static.bigideasmath.com
- Highest rating: 4
- Lowest rating: 2
- Descriptions: Exploring Parallel Lines. Work with a partner. Use dynamic geometry software to draw two parallel lines. Draw a third line that intersects both.
- More : Exploring Parallel Lines. Work with a partner. Use dynamic geometry software to draw two parallel lines. Draw a third line that intersects both.
- https://static.bigideasmath.com/protected/content/pe/hstx/sections/tx_geo_03_02.pdf
Also Check: What Is Ecosystem In Biology
Thm 34 Alternate Interior Angle If 2
understand the parallel lines cut by a transversal theorem and it’s converse. In the diagram, 22 = 26 and 23 = 27. Classify the angle pairs formed when parallel lines are cut by a transversal, as either congruent, supplementary and corresponding angles, alternate interi Converse of alternate exterior angles: 3.2 parallel lines and transversals & 3.3 proving lines parallel. If two parallel lines are cut by a transversal, then the pairs of . find angle measures using the theorem. When a transversal intersects two or more parallel lines the angle pairs we discussed in section 3.1. , then the two pairs of alternate interior angles are congruent. If two lines and a transversal form alternate exterior angles that are congruent, then the two lines . Thm 3.4 alternate interior angle if 2 . 3.2 angles formed by a transversal. If two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent.
3.2 Parallel Lines And Transversals Worksheet Answers / Parallel And Perpendicular Lines Systry –. understand the parallel lines cut by a transversal theorem and it’s converse. , then the two pairs of alternate interior angles are congruent. Classify the angle pairs formed when parallel lines are cut by a transversal, as either congruent, supplementary and corresponding angles, alternate interi find angle measures using the theorem. In the diagram, 22 = 26 and 23 = 27.
Use Parallel Lines And Transversals
Course Hero uses AI to attempt to automatically extract content from documents to surface to you and others so you can study better, e.g., in search results, to enrich docs, and more. This preview shows page 1 – 2 out of 4 pages.
Upload your study docs or become a
Course Hero member to access this document
Don’t Miss: What Is Spatial Diffusion In Human Geography
Angles In Parallel Lines
Here we will learn about angles in parallel lines including how to recognise angles in parallel lines, use angle facts to find missing angles in parallel lines, and apply angles in parallel lines facts to solve algebraic problems.
There are also angles in parallel lines worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if youre still stuck.
What Are Parallel Lines
When the distance between a pair of lines is always the same, then we call such lines as parallel lines. The symbol for parallel to is // . Parallel lines are the lines which never meet each other. For the two lines to be parallel, the most important thing is that they are drawn in the same plane. These lines are always equidistant from each other.
Recommended Reading: What Does Tyr Stand For In Biology
Parallel Lines And Transversal
Do you know what Parallel Lines are? You will understand this with the following examples. Every one of you must have seen the pair of railway tracks or a ladder or piano keys. What is one common thing among all these? The two tracks never meet each other, also the two sides of the ladder never intersect each other. The keys of the piano are always parallel to each other. Let us now study parallel and transversal lines and corresponding angles in detail.
Table of content
Use The Figure Below To Answer The Following Questions
If a transversal intersects two parallel lines, what do you know about corresponding angles?You may use the figures above to help.
If a transversal intersects two parallel lines, what do you know about alternate interior angles?You may use the figures above to help.
If a transversal intersects two parallel lines, what do you know about same-side interior angles?You may use the figures above to help.
If a transversal intersects two parallel lines, what do you know about alternate exterior angles?You may use the figures above to help.
Read Also: What Degree Do You Need For Criminal Psychology
Angle Relationships: Parallel Lines & Transversal
In geometry, lines are classified into several types such as parallel, perpendicular, intersecting and non-intersecting lines, etc. For non-intersecting lines, we can draw a special line called transversal that intersects these lines at different points. In this article, you will learn about parallel lines, transversals and angle relationships with these lines along with suitable images and examples.
Example : Alternate Angles
Calculate the size of the missing angle \theta . Justify your answer.
2State the alternate angle, co-interior angle or corresponding angle fact to find a missing angle in the diagram.
Here we can label the alternate angle on the diagram as 50^o .
3Use a basic angle fact to calculate the missing angle.
Here as \theta is on a straight line with 50^o ,
\theta =180^o-50^o
Calculate the size of the missing angle \theta . Justify your answer.
Highlight the angle that you already know.
State the alternate angle, co-interior angle or corresponding angle fact to find a missing angle in the diagram.
Here we can label the co-interior angle on the diagram as 60^o as 120+60= 180^o .
Use a basic angle fact to calculate the missing angle.
We can see that as \theta is vertically opposite to 60^o ,
\theta =60^o .
Calculate the size of the missing angle \theta . Justify your answer.
Highlight the angle that you already know.
State the alternate angle, co-interior angle or corresponding angle fact to find a missing angle in the diagram.
Here we can label the corresponding angle on the diagram as 75^o .
Use a basic angle fact to calculate the missing angle.
Here as \theta is on a straight line with 75^o ,
\theta =180-75
Calculate the size of the missing angle \theta . Show all your working.
Highlight the angle that you already know.
Use a basic angle fact to calculate the missing angle.
Opposite angles are equal so we can label the angle 110^o .
Don’t Miss: What Is Iupac In Chemistry
Parallel Lines And Transversal 1
- www.livingston.org
- Highest rating: 5
- Lowest rating: 2
- Descriptions: 3.2 Parallel Lines and Transversals. If two parallel cut by a transversal, lines are. Key. Alternate Interior Angles Theorem. Name: If two parallel.
- More : 3.2 Parallel Lines and Transversals. If two parallel cut by a transversal, lines are. Key. Alternate Interior Angles Theorem. Name: If two parallel.
- http://www.livingston.org/cms/lib9/NJ01000562/Centricity/Domain/1473/3.2%2520parallel%2520lines%2520and%2520transversal%25201.pdf
Solved Examples For You
Question 2: If l is any given line an P is any point not lying on l, then the number of parallel lines drawn through P, parallel to l would be:
Answer : The correct option is A. Draw a line l and a point P not lying on l. Now we can draw a straight line parallel to l, which passes through P. We can see that only one line is drawn which is parallel to l and passes through P.
Question 2: Identify the given angle in the diagram.
Answer : The correct option is D. The angles opposite to the sides of the transversal line and which is exterior is Alternate Exterior Angles.
Question 3: What is an example of a corresponding angle?
Answer: You already know that the transversal is when a line crosses two other lines, similarly, the angles in matching corners are referred to as corresponding angles. For instance, a and e are corresponding angles. Thus, when these two lines are parallel, the corresponding angles are equal.
Question 4: What is the sum of two corresponding angles?
Answer: As it is known that corresponding angles can be supplementary when the transversal intersects two parallel lines perpendicularly this is at 90 degrees. Thus, in such a case, each of the corresponding angles is going to be 90 degrees and their sum will add up to 180 degrees which is supplementary.
Question 5: What is a transversal?
Question 6: State the properties of a transversal.
You May Like: Geometry Unit 6 Test Answer Key
What Are Angles In Parallel Lines
Angles in parallel lines are angles that are created when two parallel lines are intersected by another line called a transversal.
We can use the information given in the diagram to find any angle around the intersecting transversal.
To do this, we use three facts about angles in parallel lines:
Alternate angles, co-Interior angles, and corresponding angles.
Properties of parallel lines
- Co-interior angles add up to 180^o:
Sometimes called C angles.
Example : Similar Triangles
Show that the two triangles are similar.
Highlight the angle that you already know.
Use a basic angle fact to calculate a missing angle.
Here, we can see that the two angles highlighted in green are on a straight line and so their sum is 180^o . This gives us the missing angle of 70^o .
We can also see there is a vertically opposite angle at the centre of the diagram. This is also 90^o .
The smaller triangle now has a missing angle of 20^o as angles in a triangle add to equal 180^o .
State the alternate angle, co-interior angle or corresponding angle fact to find a missing angle in the diagram.
You May Like: What Is Statistical Significance In Psychology