Whats The Point Of Using The Standard Error
When we calculate the mean of a given sample, were not actually interested in knowing the mean of that particular sample, but rather the mean of the larger population that the sample comes from.
However, we use samples because theyre much easier to collect data for compared to an entire population. And of course the sample mean will vary from sample to sample, so we use the standard error of the mean as a way to measure how precise our estimate is of the mean.
Youll notice from the formula to calculate the standard error that as the sample size increases, the standard error decreases:
Standard Error = s/ n
This should make sense as larger sample sizes reduce variability and increase the chance that our sample mean is closer to the actual population mean.
The Standard Error Formula
To calculate the standard error, you need to have two pieces of information: the standard deviation and the number of samples in the data set. The standard error is calculated by dividing the standard deviation by the square root of the number of samples.
Here is the full annotated standard error formula:
Finding The Variance In Your Sample
Read Also: Paris Jackson Father Biological
How To Calculate Standard Deviation
In statistics, the standard deviation is a measure that is used to quantify the amount of variation in a set of data. A standard deviatin close to 0 indicates that the data tend to be very close to the mean. A high standard deviation means that the data points are spread over a wider range of values. Standard deviation is commonly used to measure confidence in statistical conclusions.
Variance And Standard Deviation Formula

The formulas for the variance and the standard deviation is given below:
Standard Deviation Formula
The population standard deviation formula is given as:
\^2}\)
Here,
N = Number of observations in population
Xi = ith observation in the population
= Population mean
Similarly, the sample standard deviation formula is:
\^2}\)
Here,
n = Number of observations in sample
xi = ith observation in the sample
\ = Sample mean
The population variance formula is given by:
\^2\)
The sample variance formula is given by:
\^2\)
Read Also: Ct Algebra 1 Curriculum Version 3.0
Task : Using The Formula
Using this method, we have an idea of what is “normal” and what is extra large or extra small. It is basically a measure of how spread out the numbers are. Here is the formula you used it the steps above, it looks a lot scarier than it is.
Ï = the standard deviation | x = each value in the population | x= the mean of the values | N = number of values
The following scores were collected for a midterm exam given to six biology students. Use the formula to calculate the standard deviation. Show all work!
52, 68, 72, 86, 90, 98
When To Use Standard Deviation Vs Standard Error
If we are simply interested in measuring how spread out values are in a dataset, we can use the standard deviation.
However, if were interested in quantifying the uncertainty around an estimate of the mean, we can use the standard error of the mean.
Depending on your specific scenario and what youre trying to accomplish, you may choose to use either the standard deviation or the standard error.
Also Check: What Does Abiotic Mean In Biology
Example: Standard Deviation Vs Standard Error
Suppose we measure the weight of 10 different turtles.
For this sample of 10 turtles, we can calculate the sample mean and the sample standard deviation:
Suppose the standard deviation turns out to be 8.68. This gives us an idea of how spread out the weights are of these turtles.
But suppose we collect another simple random sample of 10 turtles and take their measurements as well. More than likely, this sample of 10 turtles will have a slightly different mean and standard deviation, even if theyre taken from the same population:
Now if we imagine that we take repeated samples from the same population and record the sample mean and sample standard deviation for each sample:
Now imagine that we plot each of the sample means on the same line:
The standard deviation of these means is known as the standard error.
The formula to actually calculate the standard error is:
Standard Error = s/ n
- n: sample size
Calculate The Population Standard Deviation
Read Also: Definition Of Abiotic In Biology
What Is The Standard Error
The standard error , sometimes referred to as the standard error of the mean , is a statistic that corresponds to the standard deviation of a sampling distribution, relative to the mean value. But what actually is that?
Say you are interested in the average age people in the UK are diagnosed with Alzheimers disease. It is not feasible to determine this for everyone in the UK, therefore researchers take a sample population to generalise an overall figure. For example, 10,000 British people with the disease may be analysed and will be used to generate the average age of diagnosis. If you do this on a random sample of 5,000 patients, you may get an average age of diagnosis of 61.5 years. However, if you do the sample analysis on a separate random sample of 10,000 other patients, you may get an average age of 62.3 years. Lets say, hypothetically speaking of course, that if you were able to analyse all of the people in the UK who have Alzheimers disease to get the actual figure, you may end up with 64.3 years. You can notice that the figures gained from the sample populations differs to the actual figure . This variation in mean values is expected, and as you increase the number of people in your sample population you will get a value which is closer to the actual figure. This is exactly what the standard error represents. The standard error signifies this variation in the mean values between the sample populations.
Different Ways To Calculate Standard Deviation
There are two main ways to calculate standard deviation: population standard deviation and sample standard deviation. If you collect data from all members of a population or set, you apply the population standard deviation. If you take data that represents a sample of a larger population, you apply the sample standard deviation formula. The equations/calculations are nearly the same with two exceptions: for the population standard deviation, the variance is divided by the number of data points , while for the sample standard deviation, it’s divided by the number of data points minus one .
You May Like: Imagine Math Parent Portal
Applications Of Standard Deviation
Standard deviation is widely used in experimental and industrial settings to test models against real-world data. An example of this in industrial applications is quality control for some products. Standard deviation can be used to calculate a minimum and maximum value within which some aspect of the product should fall some high percentage of the time. In cases where values fall outside the calculated range, it may be necessary to make changes to the production process to ensure quality control.
Standard deviation is also used in weather to determine differences in regional climate. Imagine two cities, one on the coast and one deep inland, that have the same mean temperature of 75°F. While this may prompt the belief that the temperatures of these two cities are virtually the same, the reality could be masked if only the mean is addressed and the standard deviation ignored. Coastal cities tend to have far more stable temperatures due to regulation by large bodies of water, since water has a higher heat capacity than land essentially, this makes water far less susceptible to changes in temperature, and coastal areas remain warmer in winter, and cooler in summer due to the amount of energy required to change the temperature of the water. Hence, while the coastal city may have temperature ranges between 60°F and 85°F over a given period of time to result in a mean of 75°F, an inland city could have temperatures ranging from 30°F to 110°F to result in the same mean.
Which Equation Do I Use

In general, if you’re analyzing data that represents a larger set, choose the sample standard deviation. If you gather data from every member of a set, choose the population standard deviation. Here are some examples:
- Population Standard DeviationAnalyzing test scores of a class.
- Population Standard DeviationAnalyzing the age of respondents on a national census.
- Sample Standard DeviationAnalyzing the effect of caffeine on reaction time on people ages 18 to 25.
- Sample Standard DeviationAnalyzing the amount of copper in the public water supply.
Recommended Reading: What Is The Molecular Geometry Of Ccl4
The Calculation Of Standard Deviation
The calculation of standard deviation for the concentration of ascorbic acid in each lemon juice is measured by using the formula below.
M = V1 + V2 + V3 + V4 + V5 x M
V1 V2 V3 V4 V5
M = the uncertainty for the concentration of ascorbic acid in the lemon juice
M = the concentration of ascorbic acid in the lemon juice
V1 = the uncertainty for the volume of D.C.P.I.P
V1 = the volume of D.C.P.I.P
V2 = the uncertainty of the volume of glacial acetic acid
V2 = the volume of glacial acetic acid
V3 = the uncertainty for the volume of appropriate lemon juice
V3 = the volume of appropriate lemon juice
V4 = the uncertainty for the volume of solution*
V4 = the volume of solution*
V5 = the uncertainty for the average volume of solution in burette
V5 = the average volume of solution in burette
An example for determining the standard deviation of the concentration of ascorbic acid in the lemon juice is shown below.
Fresh lemon juice,
M = 0.1 + 0.1 + 0.1 + 0.5 + 0.10 x 20.63
1.0 10.0 4.0 100.0 6.06
= ± 3.23 mg/100 cm³
The calculation for other standard deviation will be using the same formula as above.
Standard Error Of The Mean
SEM is calculated by taking the standard deviation and dividing it by the square root of the sample size.
Standard error gives the accuracy of a sample mean by measuring the sample-to-sample variability of the sample means. The SEM describes how precise the mean of the sample is as an estimate of the true mean of the population. As the size of the sample data grows larger, the SEM decreases versus the SD hence, as the sample size increases, the sample mean estimates the true mean of the population with greater precision. In contrast, increasing the sample size does not make the SD necessarily larger or smaller, it just becomes a more accurate estimate of the population SD.
Also Check: What Is Ph Paper Used For In Chemistry
The Average Volume Of Solution*
The average volume of solution is counted by dividing the volume ) with 5 trials. The formula is illustrated below:
Volume for cm³
The fresh lemon juice is taken as the example for this formula.
= cm³
= cm³
The calculation for the other two appropriate lemon juices will be using the same method as shown in .
But There Is A Small Change With Sample Data
Our example has been for a Population .
But if the data is a Sample , then the calculation changes!
When you have “N” data values that are:
- The Population: divide by N when calculating Variance
- A Sample: divide by N-1 when calculating Variance
All other calculations stay the same, including how we calculated the mean.
Example: if our 5 dogs are just a sample of a bigger population of dogs, we divide by 4 instead of 5 like this:
427,130165
Think of it as a “correction” when your data is only a sample.
Also Check: What Is The Molecular Geometry Of Ccl4
Confused About Standard Deviation
I’m a first year A level student studing maths, further maths, biology and chemistry.In maths, we find the standard deviation by dividing by n.In biolgy, we find the standard deviation by dividing by n-1.I’m not entirely sure why we use different formulas in the two subjects when they’re at the same level, and it’s causing quite a bit of confusion.
Thanks in advance if anyone can explain this to me.
If you have a sample – a set of $n$ observations or results or trials $\$- then the variance of the sample is
$s_n^2 = \frac 1 n \sum ^2$
However, in biology and other sciences, usually we are more interested in the statistics of the whole population rather than the sample itself. And it turns out that a better estimate of the variance of the whole population is
$s^2 = \frac 1 \sum ^2$
The correction from $n$ to $n-1$ is known as Bessel’s correction.
How Is Standard Deviation Calculated
The formula for standard deviation makes use of three variables. The first variable is the value of each point within a data set, with a sum-number indicating each additional variable . The mean is applied to the values of the variable M and the number of data that is assigned to the variable n. Variance is the average of the values of squared differences from the arithmetic mean.
To calculate the mean value, the values of the data elements have to be added together and the total is divided by the number of data entities that were involved.
Standard deviation, denoted by the symbol , describes the square root of the mean of the squares of all the values of a series derived from the arithmetic mean which is also called the root-mean-square deviation. 0 is the smallest value of standard deviation since it cannot be negative. When the elements in a series are more isolated from the mean, then the standard deviation is also large.
The statistical tool of standard deviation is the measures of dispersion that computes the erraticism of the dispersion among the data. For instance, mean, median and mode are the measures of central tendency. Therefore, these are considered to be the central first order averages. The measures of dispersion that are mentioned directly over are averages of deviations that result from the average values, therefore these are called second-order averages.
You May Like: Kendall Hunt Geometry Answer Key
Standard Deviation Vs Standard Error: Whats The Difference
Two terms that students often confuse in statistics are standard deviation and standard error.
The standard deviation measures how spread out values are in a dataset.
The standard error is the standard deviation of the mean in repeated samples from a population.
Lets check out an example to clearly illustrate this idea.
How To Calculate Standard Error
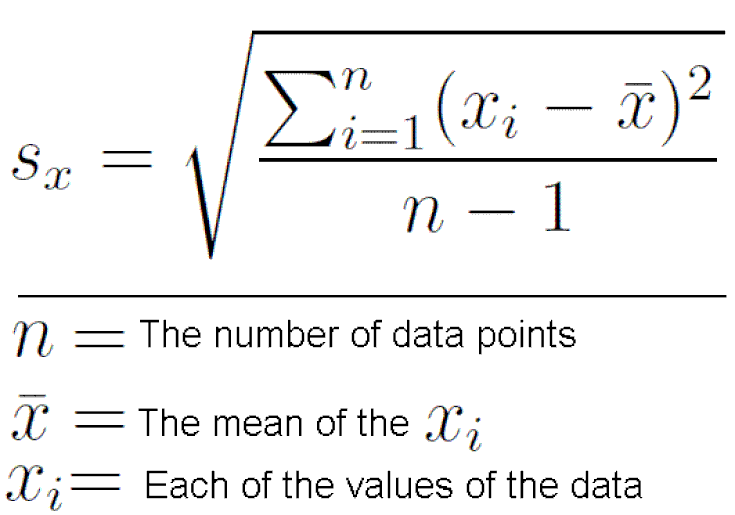
Standard error can be calculated using the formula below, where represents standard deviation and n represents sample size.
Standard error increases when standard deviation, i.e. the variance of the population, increases. Standard error decreases when sample size increases as the sample size gets closer to the true size of the population, the sample means cluster more and more around the true population mean.
Don’t Miss: Geometry Segment Addition Postulate Worksheet
Comparing Data Sets Using Statistics
Data sets can be compared using averages, box plots, the interquartile range and standard deviation.
Standard deviation is an important measure of spread or dispersion.
It tells us how far, on average the results are from the mean.
Therefore if the standard deviation is small, then this tells us that the results are close to the mean, whereas if the standard deviation is large, then the results are more spread out.
For example, the following two data sets are significantly different in nature and yet have the same mean, median and range.
Some sort of numerical measure which distinguishes between them would be useful.
| Data set 1 | |
|---|---|
| 16 | 28 |
Most of the results in data set 2 are close to the mean, whereas the results in data set 1 are further from the mean in comparison.
This suggests that the standard deviation is smaller in data set 2 than data set 1.
When comparing distributions, it is better to use a measure of spread or dispersion in addition to a measure of central tendency .
There are two formulae for calculating the standard deviation, however the most commonly used formula to calculate the standard deviation is:
Where \ means ‘sum of’
\ is the ‘mean’
\ is the number of data in the sample
Use this information to try the example questions below.
- Question