What Is A Line Segment
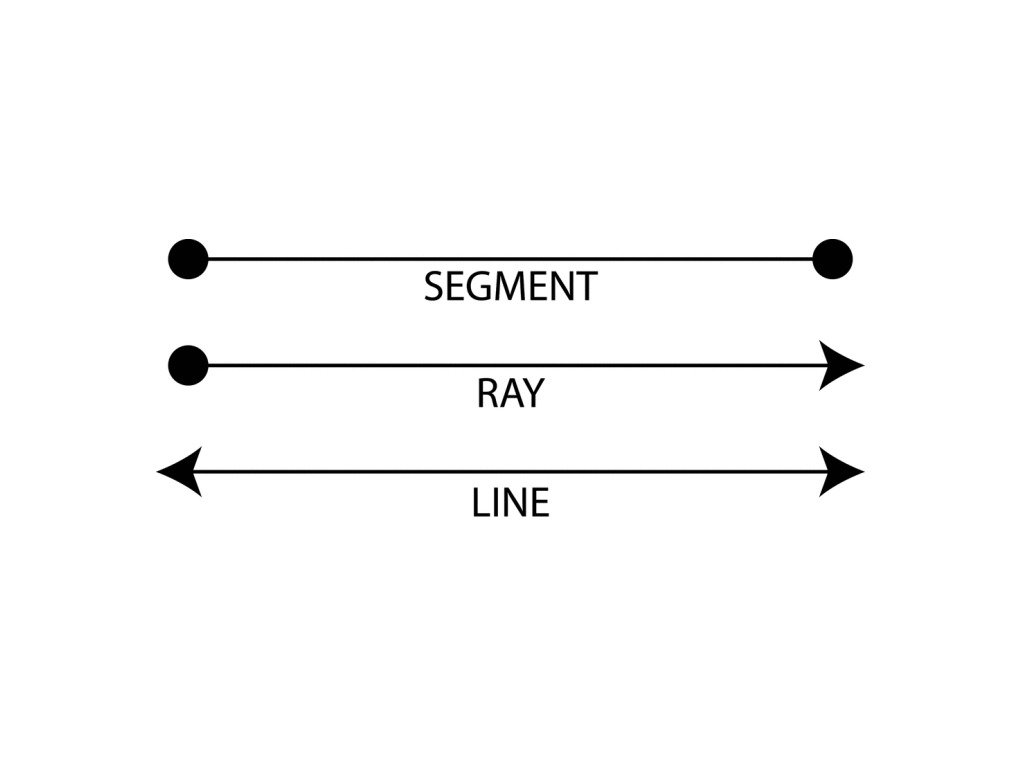
A line segment is a part of a line having two endpoints. Figures such as a triangle, polygon, hexagon, square are made of different numbers of line segments. The measure of a line segment is called its length. In contrast to the infinitely extending line, a line segment has a fixed length and can be measured easily. A line segment with A and B as two endpoints is represented as \.
| Also, read: |
Lines Segments And Rays
Although we all know intuitively what a line is, it is actually difficult to give a good mathematical definition. Roughly, we can say that a line is an infinitely thin, infinitely long collection of points extending in two opposite directions. When we draw lines in geometry, we use an arrow at each end to show that it extends infinitely.
A line can be named either using two points on the line or simply by a letter, usually lowercase .
A line segment has two endpoints. It contains these endpoints and all the points of the line between them. You can measure the length of a segment, but not of a line.
A segment is named by its two endpoints, for example, A ¯ .
A ray is a part of a line that has one endpoint and goes on infinitely in only one direction. You cannot measure the length of a ray.
A ray is named using its endpoint first, and then any other point on the ray (for example, B
How To Find The Length Of A Line Segment
In order to find the length of a line segment, we use a scale to measure its dimensions. In some cases, if the coordinates of the endpoints of the line segment are given, then we apply the distance formula, D = , where “D” is the distance between the endpoints of the line segment and , \) and , \) are the coordinates of the two points.
Also Check: Holt Geometry Practice Workbook Answer Key
Lines And Angles Definitions Properties Types Practice Questions
Ancient mathematicians introduced the concept of lines to represent straight objects which had negligible width and depth. Considered as a breadth less length by Euclid, lines form the basis of Euclidean geometry.
When two rays intersect each other in the same plane, they form an angle. The point of intersection is called a vertex.
In this article, we go over the basic properties, definitions, and types of lines and angles related to geometry. Well also look at a few examples for you to understand the properties of lines and angles in a better manner. Before we move forward, take a look at the five-step GMAT Preparation plan to score 700+ on the GMAT:
A line does not have any endpoints. It has an infinite length.
How To Measure Line Segments

Line segments can be measured with the help of a ruler . Let us see how to measure a given line segment and name it PQ.
- Step 1: Place the tip of the ruler carefully so that zero is placed at the starting point P of the given line segment.
- Step 2: Now start reading the values given on the ruler and spot the number which comes on the other endpoint Q.
- Step 3: Thus, the length of the line segment is 4 inches, which can be written as \ = 4 inches.
Don’t Miss: Who Is Paris Jacksons Mother
Difference Between Line And Line Segment
Categorized under Science | Difference Between Line and Line Segment
Line vs Line Segment
In the study of geometry and mathematics, shapes, sizes, positions, quantity, and changes are examined and analyzed. These two fields are also involved in the study of lines and line segments.
The term line comes from the Middle English word ligne which comes from the Old English word line for the Latin word linum meaning flax. It has Indo-European roots that in modern word usage have come to develop several different meanings.
The most common usage for the word line is in mathematics and geometry. A line is defined as a geometric figure that is formed by a point that moves in a fixed direction. It is the intersection of two planes, and it can go on endlessly in both directions. It is sometimes described as an infinitely long and perfectly straight curve that has an infinite number of points.
The concept of a line was introduced by mathematicians to represent straight objects that have no width and depth. It is a length that can either be straight or curved which does not have any thickness or breadth. Modern mathematicians define line in two different ways which in a sense relate to each other. One pursues Euclids approach that defines it as an abstract and archaic object that is defined by a set of principles.
Summary:
Some Other Types Of Lines In Maths
1.Tangent lines
The Tangent is a straight line which just touches the curve at a given point. The normal is a straight line which is perpendicular to the tangent. To calculate the equations of these lines, we shall make use of the fact that the equation of a straight line passing through the point with coordinates and having gradient m is given by
We also make use of the fact that if two lines with gradients m1 and m2 respectively are perpendicular, then m1m2 = 1.
Example: Suppose we wish to find points on the curve y given by \ where the tangents are parallel to the line y = x + 5.
Solution: If the tangents have to be parallel to the line then they must have the same gradient. The standard equation for a straight line is y = mx + c, where m is the gradient. So what we gain from looking at this standard equation and comparing it with the straight line y = x + 5 is that the gradient, m, is equal to 1. Thus, the gradients of the tangents we are trying to find must also have gradient 1.
We know that if we differentiate y we will obtain an expression for the gradients of the tangents to y and we can set this equal to 1. Differentiating and making it equal to 1 we find:
from which
This is a quadratic equation which we can solve by factorisation.
Don’t Miss: My Hrw Answers Algebra 1
Frequently Asked Questions Line Segments And Ray
Q.1. How are a line segment and a ray the same?Ans:A line segment is a part of a line with two endpoints, whereas a ray is also a part of a line that has \ endpoint and extends indefinitely in one direction. So, a line segment and a ray both are part of a line.
Q.2. What are a line, ray, and segment?Ans: Line: A collection of points make a line. It extends endlessly and indefinitely in both directions.Ray: A ray is part of a line with one endpoint and can be extended indefinitely in the other direction.Segment: A part of the line is called a line segment. It has \ endpoints and has a definite length, which cannot be increased or decreased.
Q.3. What is the difference between ray and line segment?Ans:A ray and a line segment both are a part of a line. The only major difference between them is that a line segment has two endpoints and thus cannot be extended in both directions and has a fixed length. In contrast, a ray has one point fixed and the other endpoint extended indefinitely in one direction.
Q.4. Can a line segment also be a ray?Ans:A line segment and a ray both are a part of a line. A line segment has two endpoints, whereas a ray has only one endpoint. So a line segment cannot be a ray, but it can be a part of a ray.
What Is A Line Segment Look Like
line segmentsegmentsegmentlinelooks likelinelineline segmentLine Segment Bisector, Right Angle
Don’t Miss: Exponential Growth And Decay Common Core Algebra 1 Homework Answer Key
In Real Or Complex Vector Spaces
If V is a vector space over R C } , and L is a subset of V, then L is a line segment if L can be parameterized as
- L +t\mathbf \mid t\in \}}
for some vectors V ,\mathbf \in V\,\!} . In which case, the vectors u and u + v are called the end points of L.
Sometimes, one needs to distinguish between “open” and “closed” line segments. In this case, one would define a closed line segment as above, and an open line segment as a subset L that can be parametrized as
- L +t\mathbf \mid t\in \}}
for some vectors ,\mathbf \in V\,\!} .
Equivalently, a line segment is the convex hull of two points. Thus, the line segment can be expressed as a convex combination of the segment’s two end points.
In geometry, one might define point B to be between two other points A and C, if the distance AB added to the distance BC is equal to the distance AC. Thus in R 2 ^} , the line segment with endpoints A = and C = is the following collection of points:
- . )^+^}}+)^+^}}=-a_)^+^}}\right\}.}
Frequently Asked Questions Lines
Q.1. What is a line called?Ans: A line has a length, but it has no width. A line is a type of geometric diagram that can move in both directions. So, it is made up of an endless number of points, and it is infinite and has no ends on both sides. A line is one-dimensional.
Q.2. What are the types of lines?Ans: The types of the lines are given below:1. Straight lines
Read Also: Who Are Paris Jackson’s Biological Parents
Measuring A Line Segment
Follow the given steps to measure the length of a line segment:
Step 1: Pick up a scale to measure the length of a line segment. Generally smaller line segments are measured using a centimeter scale.
Step 2: Identify the line segment you want to measure.
Step 3: Place the tip of the ruler at the starting point of the line segment.
Step 4: Read the number on the scale where the line segment ends. In this case, it is 5. So, the length of the given line segment is 5 cm.
Drawing A Line Segment Using Ruler And Compass

Suppose we need to draw a line segment of length 5 cm. We will follow the given steps:
-
Step 1: Draw a line of any length. Mark a point A on the line, which is the starting point of the line segment.
-
Step 2: Using a ruler, place the pointer of the compass 5 cm apart from the pencils lead.
-
Step 3: Place the pointer of the compass at A and mark an arc on the line with the pencil point.
-
Step 4: Mark the point where the arc and the line intersect as B.
-
Step 5: AB is the required line segment of length 5 cm.
Recommended Reading: Do You Capitalize Majors
What Is The Definition Of A Line Segment In Geometry
geometryline segmentlineline
In geometry, a ray is a line with a single endpoint that extends infinitely in one direction. An example of a ray is a sun ray in space the sun is the endpoint, and the ray of light continues on indefinitely.
Subsequently, question is, what is a point in math? A point in geometry is a location. It has no size i.e. no width, no length and no depth. A point is shown by a dot. A line is defined as a line of points that extends infinitely in two directions. It has one dimension, length.
Beside this, what is line and line segment?
A line segment is a straight line that passes through the two points. A line segment has a definite length. The shortest distance between two points can be measured with the help of a ruler. It has length, but it does not have a width and depth.
What is a property of an angle?
When to lines intersect they create four angles. Each angle is opposite to another and form a pair of what are called opposite angles. Angles a and c are opposite angles. Angles b and d are opposite angles. Opposite angles are equal.
What Are The Opposite Rays In Geometry
Opposite Rays are those 2 rays that start exactly from the same point but continues to the opposite direction. Take an example of the below Opposite Rays:
The start point for the Rays ZX and ZY is Z, and then they both go the opposite direction that makes 2 opposite rays: ZX and ZY.
Points to Remember about Opposite Rays
- Both Rays must Start from the same point
- Must go the opposite direction
- Must form a line
You May Like: Geometry Eoc Fsa Practice Test (calculator Portion)
Can We Extend The Line Segment
No, the line segment cannot be extended as it has two endpoints and a definite length. Whereas, we can extend the line in two opposite directions and a ray can be extended in one end.
Put your understanding of this concept to test by answering a few MCQs. Click Start Quiz to begin!
Select the correct answer and click on the Finish buttonCheck your score and answers at the end of the quiz
Definition Of A Segment
A segment is a set of points consisting of two points of the line called the endpoints, and all of the points of the line between the endpoints. It is commonly used to represent the length, height, or width of a certain object and the distance between two objects. It is named by using the label of its endpoints and insert a line ) above the letters. Figure 2 shows segment AB which can also be written as .
Example 1
Draw two points and label it as C and D.
Connect the two points straight each other.
Example 2
How many segments are there in the line below?
Read Also: Geometry Dash Demon Key Hack
As A Degenerate Ellipse
A line segment can be viewed as a degenerate case of an ellipse, in which the semiminor axis goes to zero, the foci go to the endpoints, and the eccentricity goes to one. A standard definition of an ellipse is the set of points for which the sum of a point’s distances to two foci is a constant if this constant equals the distance between the foci, the line segment is the result. A complete orbit of this ellipse traverses the line segment twice. As a degenerate orbit, this is a radial elliptic trajectory.
Measurement Of Line Segment
A ruler is an instrument used in geometry. We use a ruler to draw a line segment. We use it also to measure length of a line segment.
A ruler is generally 1 ft long and is called One foot ruler. Sometime it is simply called scale. Some rulers are six inches long and are called half foot ruler. One edge of a ruler has scales marked in inches and the other edge has scales marked in cm.
We place the ruler with its edge along the line-segment AB with the zero mark of the ruler at the start point A of the line-segment. We read the mark on the ruler at the other endpoint B of the line-segment.
Read Also: Algebra 1 Age Word Problems
What Is A Line Segment Definition And Examples
A line segment is part of a line consisting of two endpoints and all points between these endpoints. In the figure below, notice how segment AB is part of the line.
Notice also that point A and point B are what we call endpoints.Basically, if just draw a line between any two points, such as point A and point B, then you have drawn a line segment.
More examples of line segments.
What is a repeating decimal ? A repeating decimal is a decimal in which …
What is a reflex angle in geometry ? Definition and examples.
Would you prefer to share this page with others by linking to it?
What is a repeating decimal ? A repeating decimal is a decimal in which …
What is a reflex angle in geometry ? Definition and examples.
Lines In Spherical Geometry
6 minute read
Spherical geometry : A type of non-Euclidean geometry which forms a surface of a sphere
A line has a different interpretation in non-Euclidean geometry from that in Euclidean geometry. Interpretation, not the definition. A Straight line is still defined as the shortest path between two points.
Geodesic : The generalisation of the notion of a straight line to curved spaces.
There is just one more definition to go before we can discuss the geodesic in spherical geometry. It is Great Circle which represents the intersection of the sphere and a plane that passes through the centre of the same sphere. . A trivial example: longitudes on a globe are great circles and latitudes being small circles except for the equator.
If you have kept track of all the definitions above you could have guessed that the great circles are the geodesics in spherical geometry. Yes, you are almost correct.
In general, a geodesic in any curved space can be found by writing the equation for the length1 and then minimise it using some calculus. Elaborate treatment of this is difficult and lengthy to be mentioned here.
And yes, in the case of points that are extremities of a diameter there is no unique line joining them violating Euclids first postulate .
The geodesics of spherical geometry are the great circles.
You May Like: Homework 5 Angle Addition Postulate Answer Key