What Are The Steps For Simplifying Square Roots
- Step 1: Identify the radical expression, and assess whether or not you have one ore more radicals
- Step 2: If you have more than one radical, you can group them that are multiplying each other using Rule 1. You can group them under one radical
- Step 3: If there is a division of radicals, can use Rule 3 to group them under one radical
- Step 4: Once you have used Rule 1 or 3 to group radicals as much as possible, you use Rule 2, so see what part of the expression can be taken out of the radical
Ultimately, the game is group and potential “cancel” the radical from a portion of the expression numerator by the denominator in the fraction).
More About This Square Root Calculator
This calculator allows to simplify and calculate any valid square root expression, showing all the steps. You need to provide a valid expression involving radicals. For example, it could be something like ‘sqrt’, or something more complex like ‘sqrt/)’.
Once you provide a valid expression involving square roots, all you need to do is to click on the “Calculate” button, and step-by-step calculations will be provided to you.
Square root expressions usually can be simplified when there are multiplications involved, but often times they are cannot be further simplified. For example, something like \ cannot be simplified any further, but for something like \, we can certainly simplify:
How To Multiply Two Square Root Values Together
Let us say we have two numbers a and b. First, we will find the square root of the numbers a and b. Then, after finding the square root we will multiply the square roots value together. Let us understand this with a practical illustration. For example, multiply 4 ×16. The square root of 4 is 2 and the square root of 16 is 4 . Now, we will multiply the value of the square root of 4 and 16, i.e., 2 × 4 = 8. Instead, we can apply the property of square roots, a × b = ab.
Read Also: How To Find Iqr In Math
Square Root Simplification Rules
- Rule 1: This is the main rule: \
- Rule 2: A consequence from the previous rule, but useful to have it as its own rule: \
- Rule 3: Another main rule: \
We could add more rules to the list, but all of the other ones derive from these ones. When it comes to rules in Algebra, it is best to have a deep understanding of a few rules than having a loose grip of many rules.
How To Find A Square Root On A Calculator

To find the square root value of any number on a calculator, we simply need to type the number for which we want the square root and then insert the square root symbol in the calculator. For example, if we need to find the square root of 81, we should type 81 in the calculator and then press the symbol to get its square root. We will get 81 = 9.
Check:
Read Also: Algebra Equation Solver With Exponents
How To Simplify Square Root
To simplify a square root, we need to find the prime factorization of the given number. If a factor cannot be grouped, retain them under the square root symbol. The rule of simplifying square root is xy = , where, x and y are positive integers. For example: 12 = \ = 23
For fractions, there is also a similar rule: x/y = . For example: 50/10 = = 5
Square Root Calculator Fractions
The question is, can I use the same rules for a square root calculator for fractions? The answer is: absolutely. The idea is exactly the same, group radicals that are multiplying each other, and the potential remove the radical from part of the expression.
When dealing with fractions, the expression will likely be a fraction too, and you will deal with simplifications in the numerator and denominator all the same.
Read Also: What Is Circadian Rhythm Psychology
Students Struggling With All Kinds Of Algebra Problems Find Out That Our Software Is A Life
Search phrases used on 2010-08-20:
- math games 10th grade
- gr 8 science free online test ontario
- percent proportion
- algebra 2 an integrated approach chapter 10 test answers
- negative and positive free work sheet
- Free Rational Expressions Solver
- teaching fractions to 3rd grader for sats
- holt physics workbook answers
- how to solve eigenvectors on ti 83
- ks3 activities on simultaneous equations
- high school algebra formula sheet
- math worksheets factor tree
How To Find The Square Of A Number
The square of a number can be found by multiplying a number by itself. For single-digit numbers, we can use multiplication tables to find the square, while in the case of two or more than two-digit numbers, we perform multiplication of the number by itself to get the answer. For example, 9 × 9 = 81, where 81 is the square of 9. Similarly, 3 × 3 = 9, where 9 is the square of 3.
The square of a number is written by raising the exponent to 2. For example, the square of 3 is written as 32 and is read as “3 squared”. Here are some examples:
- 42 = 4 × 4 = 16
- 2 = 5/3 × 5/3 = 25/9
Don’t Miss: What Does Oh Mean In Chemistry
Square Root By Long Division Method
Long Division is a method for dividing large numbers into steps or parts, breaking the division problem into a sequence of easier steps. We can find the exact square root of any given number using this method. Let us understand the process of finding square root by the long division method with an example. Let us find the square root of 180.
- Step 1: Place a bar over every pair of digits of the number starting from the units’ place . We will have two pairs, i.e., 1 and 80
- Step 2: We divide the left-most number by the largest number whose square is less than or equal to the number in the left-most pair.
Step 3: Bring down the number under the next bar to the right of the remainder. Add the last digit of the quotient to the divisor. To the right of the obtained sum, find a suitable number which, together with the result of the sum, forms a new divisor for the new dividend that is carried down.
Step 4: The new number in the quotient will have the same number as selected in the divisor. The condition is the same as being either less than or equal to the dividend.
Step 5: Now, we will continue this process further using a decimal point and adding zeros in pairs to the remainder.
Step 6: The quotient thus obtained will be the square root of the number. Here, the square root of 180 is approximately equal to 13.4 and more digits after the decimal point can be obtained by repeating the same process as follows.
Example Question #: Square Roots
Evaluate the radical:
Correct answer:
In order to get the most simplified answer, do not multiply all the numbers together and combine as one radical.
Rewrite each radicals in their most simplified form.
Multiply the terms.
Notice that multiplying a square root of a number by itself will leave only the integer and will eliminate the radical.
The terms become:
Recommended Reading: What Is Corrosion In Chemistry
Key Strategy In Solving Quadratic Equations Using The Square Root Method
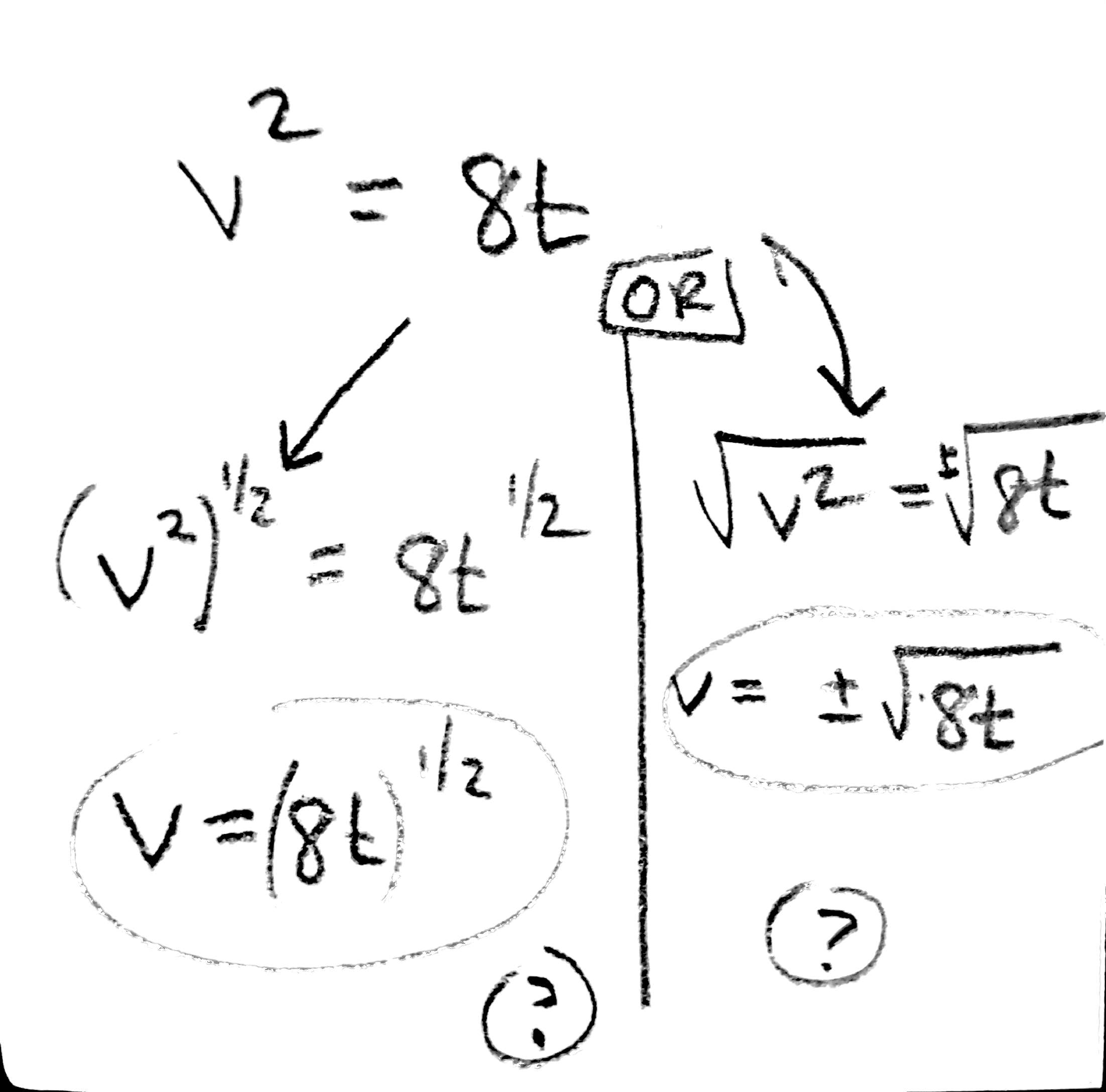
The general approach is to collect all terms on one side of the equation while keeping the constants to the opposite side. After doing so, the next obvious step is to take the square roots of both sides to solve for the value of x. Always attach the \pm symbol when you get the square root of the constant.
A Fun Way To Calculate A Square Root

There is a fun method for calculating a square root that gets more and more accurate each time around:
| a) start with a guess | |
| b) divide by the guess c) add that to the guess d) then divide that result by 2, in other words halve it. e) now, set that as the new guess, and start at b) again |
- Our first attempt got us from 4 to 3.25
- Going again gets us: 3.163
- Going again gets us: 3.1623
And so, after 3 times around the answer is 3.1623, which is pretty good, because:
3.1623 x 3.1623 = 10.00014
Now … why don’t you try calculating the square root of 2 this way?
Read Also: What Kind Of Math Is On The Sat
Square Root By Estimation Method
Estimation and approximation refer to a reasonable guess of the actual value to make calculations easier and more realistic. This method helps in estimating and approximating the square root of a given number. Let us use this method to find 15. Find the nearest perfect square numbers to 15. 9 and 16 are the perfect square numbers nearest to 15. We know that 16 = 4 and 9 = 3. This implies that 15 lies between 3 and 4. Now, we need to see if 15 is closer to 3 or 4. Let us consider 3.5 and 4. Since 3.52 = 12.25 and 42= 16. Thus, 15 lies between 3.5 and 4 and is closer to 4.
Let us find the squares of 3.8 and 3.9. Since 3.82 = 14.44 and 3.92 = 15.21. This implies that 15 lies between 3.8 and 3.9. We can repeat the process and check between 3.85 and 3.9. We can observe that 15 = 3.872.
This is a very long process and time-consuming.
What Is Square Root
The square root of a number is that factor of a number which when multiplied by itself gives the original number. Squares and square roots are special exponents. Consider the number 9. When 3 is multiplied by itself, it gives 9 as the product. This can be written as 3 × 3 or 32. Here, the exponent is 2, and we call it a square. Now when the exponent is 1/2, it refers to the square root of the number. For example, n = n1/2, where n is a positive integer.
Recommended Reading: How To Find Math Worksheet Answers
How To Get Rid Of A Square Root In An Equation
When you first learned about squared numbers like 32, 52 and x2, you probably learned about a squared number’s inverse operation, the square root, too. That inverse relationship between squaring numbers and square roots is important, because in plain English it means that one operation undoes the effects of the other. That means that if you have an equation with square roots in it, you can use the “squaring” operation, or exponents, to remove the square roots. But there are some rules about how to do this, along with the potential trap of false solutions.
TL DR
To solve an equation with a square root in it, first isolate the square root on one side of the equation. Then square both sides of the equation and continue solving for the variable. Don’t forget to check your work at the end.
What Is The Square Root Of 1
There are several ways of seeing that the square root of 1 is equal to 1. One way is by definition: the square number of a given number x is such that when you square you get the given number x.
In this case, the given number is x = 1. Notice that 1² = 1, so then 1 is the square root of 1. Another way to see it is from 1² = 1, we apply square root, so we get \, by Rule 2.
Recommended Reading: Crash Course Geometry John Green
Square Root By Prime Factorization Method
Prime factorization of any number means to represent that number as a product of prime numbers. To find the square root of a given number through the prime factorization method, we follow the steps given below:
- Step 1: Divide the given number into its prime factors.
- Step 2: Form pairs of similar factors such that both factors in each pair are equal.
- Step 3: Take one factor from the pair.
- Step 4: Find the product of the factors obtained by taking one factor from each pair.
- Step 5: That product is the square root of the given number.
Let us find the square root of 144 by this method.
This method works when the given number is a perfect square number.
Use Square Roots In Applications
As you progress through your college courses, youâll encounter formulas that include square roots in many disciplines. We have already used formulas to solve geometry applications.
We will use our Problem Solving Strategy for Geometry Applications, with slight modifications, to give us a plan for solving applications with formulas from any discipline.
You May Like: How To Test For Pure Water Chemistry
How To Solve Square Root Problems
This article was co-authored by David Jia. David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelors degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.There are 11 references cited in this article, which can be found at the bottom of the page. This article has been viewed 314,238 times.
While the intimidating sight of a square root symbol may make the mathematically-challenged cringe, square root problems are not as hard to solve as they may first seem. Simple square root problems can often be solved as easily as basic multiplication and division problems. More complex square root problems, on the other hand, can require some work, but with the right approach, even these can be easy. Start practicing square root problems today to learn this radical new math skill!
Square Root Of A Negative Number
The square root of a negative number cannot be a real number, since a square is either a positive number or zero. But complex numbers have the solutions to the square root of a negative number. The principal square root of -x is: = ix. Here, i is the square root of -1.
For example: Take a perfect square number like 16. Now, let’s see the square root of -16. There is no real square root of -16. = 16 × = 4i = i), where ‘i’ is represented as the square root of -1. So, 4i is a square root of -16.
Also Check: How Does The Internet Work Physics
Repeated Subtraction Method Of Square Root
This is a very simple method. We subtract the consecutive odd numbers from the number for which we are finding the square root, till we reach 0. The number of times we subtract is the square root of the given number. This method works only for perfect square numbers. Let us find the square root of 16 using this method.
You can observe that we have subtracted 4 times. Thus,16 = 4
Quickly Estimating Imperfect Squares
Don’t Miss: What Is Associate Of Arts In Psychology
Example: What Happens When We Square
Answer:
When we square a negative number we get a positive result.
Just the same as squaring a positive number:
Asquare root goes the other way:
3 squared is 9, so a square root of 9 is 3
A square root of a number is …
multiplied by itself
A square root of 9 is …
3when 3 is multiplied by itself9
It is like asking:
What can we multiply by itself to get this?
|
To help you remember think of the root of a tree: “I know the tree, but what root made it?“ In this case the tree is “9”, and the root is “3”. |
Here are some more squares and square roots:
| 4 |
It also works for decimal numbers.
Try the sliders below :
Using the sliders:
- What is the square root of 8?
- What is the square root of 9?
- What is the square root of 10?
- What is 1 squared?
We discovered earlier that we can square negative numbers: