Use The Quotient Rule To Divide Exponential Expressions
Lets look at dividing terms containing exponential expressions. What happens if you divide two numbers in exponential form with the same base? Consider the following expression.
\displaystyle \frac^}}^}}
You can rewrite the expression as: \displaystyle \frac. Then you can cancel the common factors of 4 in the numerator and denominator: \displaystyle
Finally, this expression can be rewritten as 4^ using exponential notation. Notice that the exponent, 3, is the difference between the two exponents in the original expression, 5 and 2.
So, \displaystyle \frac^}}^}}=4^=4^.
Be careful that you subtract the exponent in the denominator from the exponent in the numerator.
So, to divide two exponential terms with the same base, subtract the exponents.
What Is An Exponent
As we begin our study of pre-algebra and algebraic expressions, you will need to learn and understand the use of exponents. So, let’s begin by defining the term exponent.
An exponent is a number that represents the “shortcut method” to showing how many times a number is multiplied by itself.
That sounds complicated, so let’s look at a few examples:
What Is An Exponent In Mathexponents Examples
What is an exponent? An exponent is something that tells you how many times to multiply a number by itself in a sum. An exponent can also be called an index or a power. Exponents are placed to the top right of a base number. This base number is the number being multiplied by itself a certain amount of times.
You May Like: Unit 1 Geometry Basics Segment Addition Postulate
Raise Powers To Powers
Another word for exponent is power. You have likely seen or heard an example such as 3^5 can be described as 3 raised to the 5th power. In this section we will further expand our capabilities with exponents. We will learn what to do when a term with a power is raised to another power, and what to do when two numbers or variables are multiplied and both are raised to an exponent. We will also learn what to do when numbers or variables that are divided are raised to a power. We will begin by raising powers to powers.
Lets simplify \left^. In this case, the base is 5^2 and the exponent is 4, so you multiply 5^ four times: \left^=5^\cdot5^\cdot5^\cdot5^=5^ .
\left^ is a power of a power. It is the fourth power of 5 to the second power. And we saw above that the answer is 5^. Notice that the new exponent is the same as the product of the original exponents: 2\cdot4=8.
So, \left^=5^=5^ .
Likewise, \left^=x^=x^
This leads to another rule for exponentsthe Power Rule for Exponents. To simplify a power of a power, you multiply the exponents, keeping the base the same. For example, \left^=2^.
What Are Exponents In Algebra
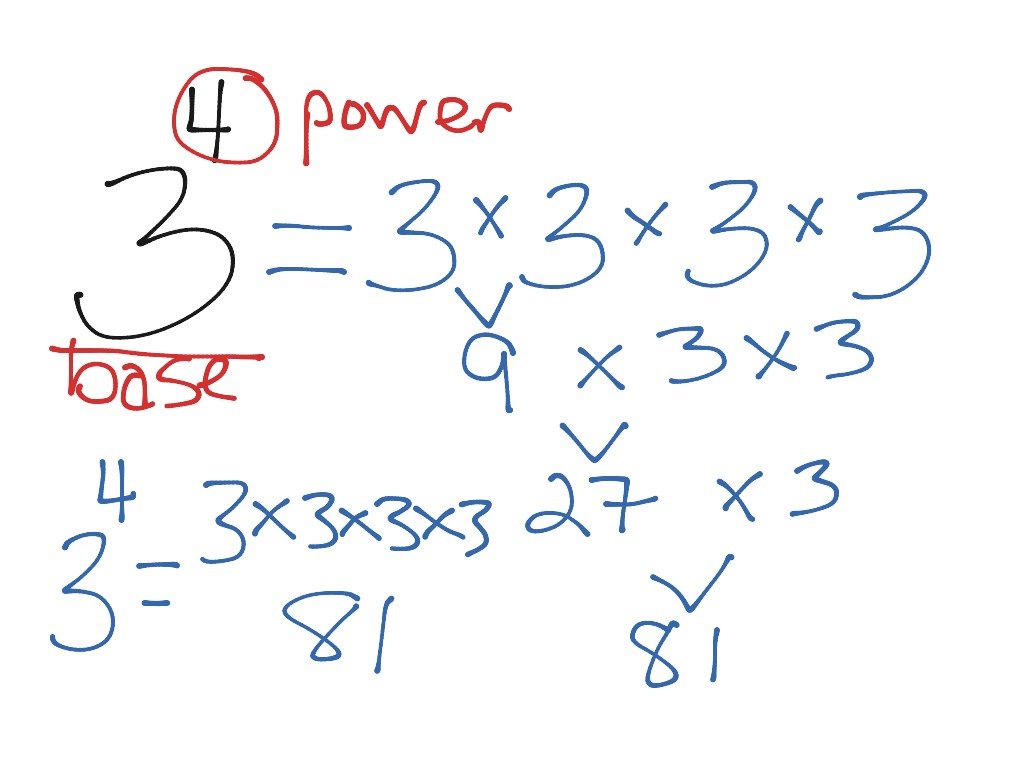
An exponent is a number that is placed as a superscript over a number. In other words, it indicates that the base is raised to a certain power. The exponent is also called by other names like index and power.If m is a positive number and n is its exponent, then mn means m is multiplied by itself for n times.
Don’t Miss: Mcgraw Hill Geometry Answer Key
Anatomy Of Exponential Terms
We use exponential notation to write repeated multiplication. For example 10\cdot10\cdot10 can be written more succinctly as 10^. The 10 in 10^ is called the base. The 3 in 10^ is called the exponent. The expression 10^ is called the exponential expression. Knowing the names for the parts of an exponential expression or term will help you learn how to perform mathematical operations on them.
\text\rightarrow10^}
10^ is read as 10 to the third power or 10 cubed. It means 10\cdot10\cdot10, or 1,000.
8^ is read as 8 to the second power or 8 squared. It means 8\cdot8, or 64.
5^ is read as 5 to the fourth power. It means 5\cdot5\cdot5\cdot5, or 625.
b^ is read as b to the fifth power. It means \cdot\cdot\cdot\cdot. Its value will depend on the value of b.
The exponent applies only to the number that it is next to. Therefore, in the expression xy^, only the y is affected by the 4. xy^ means \cdot\cdot\cdot\cdot. The x in this term is a coefficient of y.
If the exponential expression is negative, such as 3^, it means \left or 81.
If 3 is to be the base, it must be written as \left^, which means 3\cdot3\cdot3\cdot3, or 81.
Likewise, \left^=\left\cdot\left\cdot\left\cdot\left=x^, while x^=\left.
You can see that there is quite a difference, so you have to be very careful! The following examples show how to identify the base and the exponent, as well as how to identify the expanded and exponential format of writing repeated multiplication.
What Does E+ Mean In Math
4.1/5emeansnumbernumberemeansseen here
On a calculator display, E stands for exponent of 10, and it’s always followed by another number, which is the value of the exponent. For example, a calculator would show the number 25 trillion as either 2.5E13 or 2.5e13. In other words, E is a short form for scientific notation.
Additionally, what does 1e 03 mean? in generally e+03 means exponential base 10,here e+03 means 1000 the value for 9.4817e+03 means 9.4817*1000 and the value is 9481.7 Tracie Lin on 5 Feb 2019. ×
Additionally, what does the E stand for in math?
e The number e is one of the most important numbers in mathematics. It is often called Euler’s number after Leonhard Euler . e is an irrational number .
What E means?
Scientific Notation. In scientific notation, the letter E is used to mean “10 to the power of.” For example, 1.314E+1 means 1.314 * 101 which is 13.14 .
You May Like: Math Nation Section 2 Test Yourself Answers
The Law That Xm/n =nxm =m
OK, this one is a little more complicated!
I suggest you read Fractional Exponents first, so this makes more sense.
Anyway, the important idea is that:
x1/n = The n-th Root of x
And so a fractional exponent like 43/2 is really saying to do a cube and a square root , in any order.
Just remember from fractions that m/n = m × :
Example: 24 = 2 2 2 2 = 16
- In words: 24 could be called “2 to the fourth power” or “2 to the power 4” or simply “2 to the 4th”
Exponents make it easier to write and use many multiplications
Example: 96 is easier to write and read than 9 × 9 × 9 × 9 × 9 × 9
You can multiply any number by itself as many times as you want using exponents.
Try here:
| an tells you to multiply a by itself,so there are n of those a‘s: |
Recommended Reading: Does Kamala Harris Have Children
Basic Rules For Exponentiation
If $n$ is a positive integer and $x$ is any real number, then $x^n$ corresponds to repeated multiplication \begin x^n = \underbrace_}.\endWe can call this $x$ raised to the power of $n$,$x$ to the power of $n$, or simply $x$ to the $n$. Here, $x$ is the base and $n$ is the exponent or the power.
From this definition, we can deduce some basic rules that exponentiation must follow as well as some hand special cases that follow from the rules. In the process, we’ll define exponentials $x^a$ for exponents $a$ that aren’t positive integers.
The rules and special cases are summarized in the following table. Below, we give details for each one.
| Rule or special case | |
|---|---|
| $x^ax^b = x^$ | $2^22^3 = 2^5=32$ |
| $\displaystyle \frac = x^$ | $\displaystyle \frac = 2^1 =2$ |
| $^b = x^$ | $^2 = 2^6=64$ |
| $^a = x^ay^a$ | $36=6^2=^2 = 2^2\cdotbadbreak 3^2=4 \cdotbadbreak 9=36$ |
| $\displaystyle x^=\frac$ | $\displaystyle 2^=\frac$ |
| $\displaystyle x^ = \frac$ | $\displaystyle 2^ = \frac = \frac$ |
| $x^ = \sqrt = ^m$ | $4^ = ^3=2^3=8$ |
The rules
Product of exponentials with same base
If we take the product of two exponentials with the same base, we simply add the exponents:\beginx^ax^b = x^. \label\end
To see this rule, we just expand out what the exponents mean. Let’s start out with a couple simple examples.\begin 3^4 3^2 & = \times \\& = 3 \times 3 \times 3 \times 3 \times 3 \times 3\\& = 3^6\end\begin y^2 y^3 & = \times \\& = y \times y \times y \times y \times y\\& = y^5\end
Quotient of exponentials with same base
Simplify Expressions With Negative Exponents
Now we will add the last layer to our exponent simplifying skills and practice simplifying compound expressions that have negative exponents in them. It is standard convention to write exponents as positive because it is easier for the user to understand the value associated with positive exponents, rather than negative exponents.
Use the following summary of negative exponents to help you simplify expressions with negative exponents.
Don’t Miss: Does Kamala Harris Have Any Biological Children
Examples Of Exponent In A Sentence
exponentsexponentexponent Forbesexponent New York Timesexponent The Atlanticexponent Forbesexponent Popular Mechanicsexponent Quanta Magazineexponent Forbesexponent Popular Mechanics
These example sentences are selected automatically from various online news sources to reflect current usage of the word ‘exponent.’ Views expressed in the examples do not represent the opinion of Merriam-Webster or its editors. Send us feedback.
This Kind Of Situation Is So Stressful And With The Help Of Some Exceptional Algebra
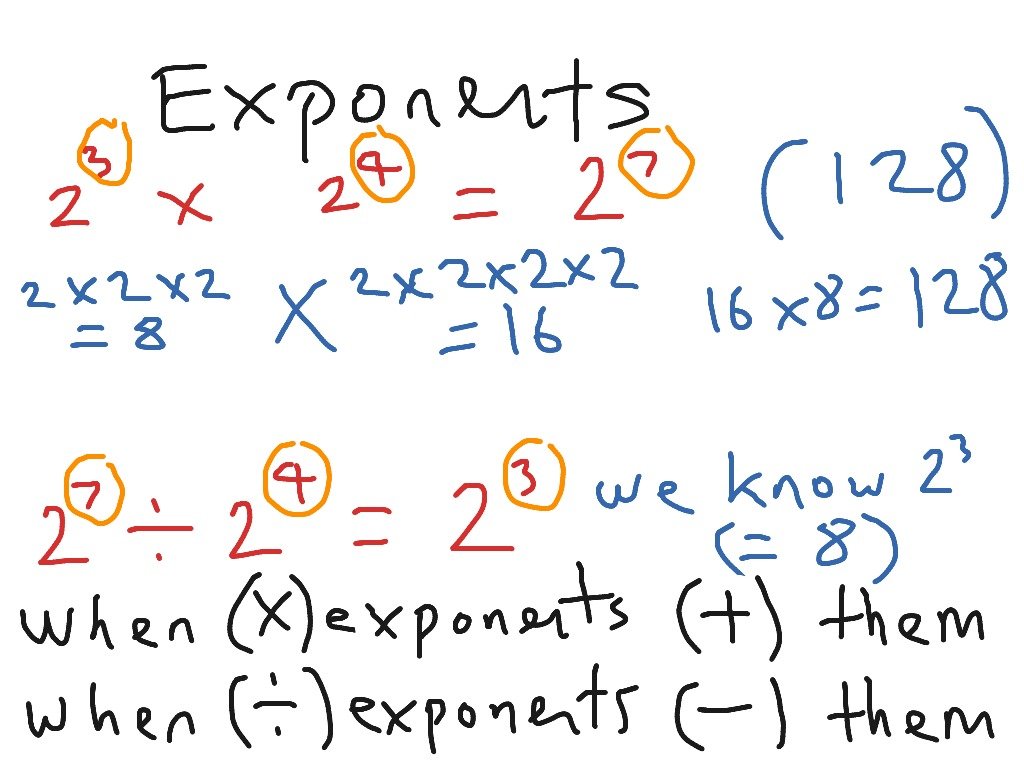
Pre algebra exponent rules worksheet. RULES OF EXPONENTS Rule 1. Any base except 0 raised to the zero power is equal to one. Your answer should contain only positive exponents.
Write the exponents as numbers in expanded form and standard form. The rule states that you can divide two powers with the same base by subtracting the exponents. 1 3235 _____ 2 43 48 _____.
Well help Improve your math test scores. These evaluating exponential functions worksheets should be your pick if you are looking for substantial practice. Polynomials Exponent Rules 1 with negative exponents Polynomials Exponent Rules 2 with negative exponents.
Quotient Rule a m a n a m-n Upgrade your skills in solving problems involving quotient rule by practicing these printable worksheets. Algebra Exponent Rules Worksheet It really is tedious as soon as your youngsters ask you in aiding these algebra house works and you are unable to accomplish this home operates or you may not find out about them in which you have not carried out algebra in your higher school days and nights. Worksheet by Kuta Software LLC 17 Exponent Rules Name_____ ID.
Some of the worksheets for this concept are Exponent rules practice Exponent rules pre algebra e1 Exponents and division Power rule Infinite pre algebra Guided notes for lesson properties of exponents Applying the exponent rule for zero exponents Powers of products and quotients. Exponents Worksheets Exponent Worksheets Algebra Worksheets. Exponent Rule Pre Algebra 1.
Also Check: Is Michael Jackson The Biological Father Of Paris Jackson
Math : What Is An Exponent And How Do You Solve It
While studying for the math section, you may have heard of an exponent as something to the power of. For example, in the expression 42 the problem is asking you to find 4 to the 2nd power.
Power refers to the number of times you multiply, not what Superman uses to fight off villains.
Tumblr
So whats the difference between exponents and regular multiplication?
Powers / Exponents Of 10
Exponents examples involving 10 as the base number crop up fairly frequently in Math and other Scientific subjects. Where 10 is multiplied by itself a number of times. It works out that a positive exponent number of 10 , in fact tells us how many 0 ‘s come after the 1 in the whole number result.
1010
Read Also: How Did Geography Affect Greece Development
Use The Product Rule To Multiply Exponential Expressions
Exponential notation was developed to write repeated multiplication more efficiently. There are times when it is easier or faster to leave the expressions in exponential notation when multiplying or dividing. Lets look at rules that will allow you to do this.
For example, the notation 5^ can be expanded and written as 5\cdot5\cdot5\cdot5, or 625. And dont forget, the exponent only applies to the number immediately to its left, unless there are parentheses.
What happens if you multiply two numbers in exponential form with the same base? Consider the expression ^^. Expanding each exponent, this can be rewritten as \left\left or 2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot2. In exponential form, you would write the product as 2^. Notice that 7 is the sum of the original two exponents, 3 and 4.
What about ^^? This can be written as \left\left=x\cdot\cdot\cdot\cdot\cdot\cdot\cdot or x^. And, once again, 8 is the sum of the original two exponents. This concept can be generalized in the following way:
Power Raised To A Power
According to this law, if a is the base, then the power raised to the power of base a gives the product of the powers raised to the base a, such as
- n = amn
where a is a non-zero term and m and n are integers.
Example 4: Express 83 as a power with base 2.
Solution: We have, 2×2×2 = 8 = 23
Therefore, 83= 3 = 29
You May Like: Geometry Textbook Mcdougal Littell Answers
S Of An Exponential Number Or Expression
For instance, how would you write 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 in exponential notation?
The number 2 is the number being multiplied repeatedly and so it automatically becomes the base of the exponential expression. Notice that it is written five times. This value specifies the number of occurrences of the base, thus, this must be the exponent.
Read as 2 to 5th power.
The base of an exponential expression can also be a letter or variable. Suppose we have
Since the variable x is multiplying itself ten times, we can write this in a compact form.
Read as x to the 10th power.
What Are The Real
Exponents have various applications. Few exponents applications are listed below:
- Exponents are widely used in computer games, measuring scales.
- Scientific scales like the pH scale or the Richter scale are based on exponents.
- Exponents are used while calculating the area, volume, and problems related to measurement.
- Exponents are most commonly used in the respective field of Science, Engineering, Economics, Accounting, Finance.
- Exponents are often used to represent a computer’s or laptop’s memory.
Recommended Reading: Span Meaning Linear Algebra
What Are Exponents And Roots
What are exponents and roots? Well, exponents are tricky little buggers when it comes to math. They are used in a ton of places from math to science and even the social sciences. The tricky part is that they seem so simple at first and then, WHAM! you suddenly have all these rules and properties that you are supposed to know, especially when it comes to roots. Luckily, we are going to discuss not only what exponents and roots are but also how to make them work for you!
Exponents And The Rules For Exponents

A number raised to a power represents a product where the same number is used as a repeated factor. The number is called the base and the power is given by the exponent. The base is the repeated factor and the exponent counts the number of factors. An exponent means that we are dealing with products and multiplication.
In the expression bn, b is the base and n is the exponent.
This expression means we use b as the factor and we have n factors of b. For example:
53 means we have 3 factors of 5, or 5*5*5 which simplifies to 125.
53 is the exponent form,5*5*5 is the expanded form, and125 is the product or simplified form.
| Exponent Form | |
|---|---|
| 3*3*3*3*3 | 243 |
| x3 |
When we calculate using numbers in exponent form that have the same base, we can always convert to expanded form, count the number of factors, then change back to exponent form, especially when the base is a variable. But this is a pain, so mathematicians have developed shortcuts, called RULES, to make the calculations quicker and easier to write.
Don’t Miss: Meaning Of Multiples In Math
The Product Rule For Exponents
For any number x and any integers a and b, \left\left = x^.
To multiply exponential terms with the same base, add the exponents.
Caution! When you are reading mathematical rules, it is important to pay attention to the conditions on the rule. For example, when using the product rule, you may only apply it when the terms being multiplied have the same base and the exponents are integers. Conditions on mathematical rules are often given before the rule is stated, as in this example it says For any number x, and any integers a and b.
Scientific Notation With Exponents
Scientific notation is the standard form of writing very large numbers or very small numbers. In this, numbers are written with the help of decimal and powers of 10. A number is said to be written in scientific notation when a number from 0 to 9 is multiplied by a power of 10. In the case of a number greater than 1, the power of 10 will be a positive exponent, while in the case of numbers less than 1, the power of 10 will be negative. Let’s understand the steps for writing numbers in scientific notation:
- Step 1: Put a decimal point after the first digit of the number from the right. If there is only one digit in a number excluding zeros, then we don’t need to put decimal.
- Step 2: Multiply that number with a power of 10 such that the power will be equal to the number of times we shift the decimal point.
To learn more about the use of exponents in writing scientific notation of numbers, visit the following articles:
Also Check: Is Physics Harder Than Chemistry
What Is The Use Of The Properties Of Exponents
There is a major use of properties of exponents in mathematics, especially in algebra. With the help of properties of exponents, we can easily simplify the expressions and also write the expressions in fewer steps. Let us understand this with a simple example. With the help of exponents properties, 24× 26 can be simplified in two quick steps as 24× 26 = 2 = 210.