What Is A Plane
A plane, in geometry, prolongs infinitely in two dimensions. It has no width. We can see an example of a plane in coordinate geometry. The coordinates define the position of points in a plane.
In Maths, a plane is a flat, two-dimensional surface that prolongs infinitely far. A plane is a two-dimensional analogue that could consist of a point, a line and three-dimensional space. Planes can appear as subspaces of a few higher-dimensional spaces, like the rooms walls extended exceptionally far away. These walls experience an independent existence on their own, as in the framework of Euclidean geometry.
What is a point?
A point is a location in a plane that has no size, i.e. no width, no length and no depth.
What is a line?
A line is a set of points that stretches infinitely in opposite directions. It has only one dimension, i.e., length. The points that lie on the same line are called collinear points.
Parallel And Perpendicular Lines
There are two types of lines that are particularly interesting and/or useful in mathematics.Parallel lines never meet or intersect. They simply go on forever side by side, a bit like railway lines. The convention for showing that lines are parallel in a diagram is to add feathers, which look like arrow heads.
Perpendicular lines intersect at a right angle, 90°:
Points: A Special Case: No Dimensions
A point is a single location in space. It is often represented by a dot on the page, but actually has no real size or shape.
You cannot describe a point in terms of length, width or height, so it is therefore non-dimensional. However, a point may be described by co-ordinates. Co-ordinates do not define anything about the point other than its position in space, in relation to a reference point of known co-ordinates. You will come across point co-ordinates in many applications, such as when you are drawing graphs, or reading maps.
Almost everything in geometry starts with a point, whether its a line, or a complicated three-dimensional shape.
You May Like: Kendall Hunt Geometry Answer Key
Example Of Plane In Geometry
We can understand planes with few examples, like walls in our room or our books or tables.
- Take your physics book , and just keep it on the table.
- Now the book is closed and it is a plane.
- Take another book and hold above the first book
- The height is equal at all the corners.
Take your physics book, and just keep it on the table. Now the book is closed and you touch its surface. This is nothing but a part of the plane. If you imagine that this surface is not limited to the book itself, just increase the surface far, you will get a plane.
You can do the same with the wall. Just extend the wall and you will see the plane!
If you imagine that this surface is not limited to the book itself, just increase the surface far, you will get a plane.
You can do the same with the wall. Just extend the wall and you will see the plane!
What Is Abc Geometry
ABCABCABC
. In this manner, what does ABC mean in geometry?
The size of an angle is measured in degrees . When we say ‘the angle ABC‘ we mean the actual angle object. If we want to talk about the size, or measure, of the angle in degrees, we should say ‘the measure of the angle ABC‘ – often written mABC.
Also Know, what are the symbols in geometry? Table of symbols in geometry:
| Symbol | |
|---|---|
| equivalence of geometric shapes and size | |
| ~ | same shapes, not same size |
Secondly, what is the measure of angle ABC?
Answer Expert VerifiedOption: A is the correct answer. The measure of ABC is 60°.
What is the symbol for plane in geometry?
The light gray symbol that looks like a very thin box represents a plane. Imagine the plane to be as thin as possible. Although the plane looks rectangular and appears to have an edge, imagine it extending as a flat surface forever. A plane would be called a two dimensional element in geometry.
You May Like: Geometry Segment Addition Postulate Worksheet
Properties Of A Plane In Geometry
There are few properties of plane, few of them are stated below,
- If there are three non-collinear points, a plane will be formed.
- If two straight lines are parallel, both these lines can for a plane.
- If two lines intersect, then also a plane can be formed.
- If you draw a line, and simultaneously one point you draw which is not on that line, then this line and point can form a plane.
- Collinear points along with one single point which not in the same line as collinear points, will form a plane.
- If you draw a line, that will be parallel to a plane or it will intersect to the plane at a point.
- If you take two or three different lines, and all are perpendicular to a plane, then these lines should be parallel.
- If two different planes, perpendicular to a line, then both the planes should be parallel.
In the geometry, we need to use a segment of planes, so we use plane figure instead of plane and it can be various shapes, like
Pointnormal Form And General Form Of The Equation Of A Plane
In a manner analogous to the way lines in a two-dimensional space are described using a point-slope form for their equations, planes in a three dimensional space have a natural description using a point in the plane and a vector orthogonal to it to indicate its “inclination”.
Specifically, let r0 be the position vector of some point P0 = , and let n = be a nonzero vector. The plane determined by the point P0 and the vector n consists of those points P, with position vector r, such that the vector drawn from P0 to P is perpendicular to n. Recalling that two vectors are perpendicular if and only if their dot product is zero, it follows that the desired plane can be described as the set of all points r such that
- n
- }=}_+s}+t},}
where s and t range over all real numbers, v and w are given linearly independentvectors defining the plane, and r0 is the vector representing the position of an arbitrary point on the plane. The vectors v and w can be visualized as vectors starting at r0 and pointing in different directions along the plane. The vectors v and w can be perpendicular, but cannot be parallel.
Read Also: Angle Addition Postulate Worksheet Answers
Line Segments And Rays
There are two kinds of lines: those that have a defined start- and endpoint and those that go on for ever.
Lines that move between two points are called line segments. They start at a specific point, and go to another, the endpoint. They are drawn as a line between two points, as you would probably expect.
The second type of line is called a ray, and these go on forever. They are often drawn as a line starting from a point with an arrow on the other end:
What Is The Meaning Of Plane Geometry
In mathematics, a plane is a flat, two-dimensional surface that extends infinitely far. A plane is the two-dimensional analogue of a point , a line and three-dimensional space.
Furthermore, what is a plane in geometry examples?
A plane extends infinitely in two dimensions. An example of a plane is a coordinate plane. A plane is named by three points in the plane that are not on the same line. Here below we see the plane ABC. A space extends infinitely in all directions and is a set of all points in three dimensions.
Also, what is another name for a plane geometry? Other names for plane A are plane BCD and plane CDE. b. Points C, E, and D lie on the same line, so they are collinear. Points B, C, E, and D lie in the same plane, so they are coplanar.
Furthermore, is plane geometry the same as geometry?
The world around us is obviously three-dimensional, having width, depth and height, Solid geometry deals with objects in that space such as cubes and spheres. Plane geometry deals in objects that are flat, such as triangles and lines, that can be drawn on a flat piece of paper.
How do you define a plane?
In mathematics, a plane is a flat, two-dimensional surface that extends infinitely far.
Planes embedded in three-dimensional Euclidean space
Read Also: Exponent Rules Worksheet 8th Grade
Point Line Plane And Solid
A Point has no dimensions, only positionA Line is one-dimensionalA Plane is two dimensional A Solid is three-dimensional
Plane vs Plain
In geometry a “plane” is a flat surface with no thickness.
But a “plain” is a treeless mostly flat expanse of land … it is also flat, but not in the pure sense we use in geometry.
Both words have other meanings too:
- Plane can also mean an airplane, a level, or a tool for cutting things flat
- Plain can also mean without special things, or well understood
What Does Picture Plane Mean In Art
In painting, photography, graphical perspective and descriptive geometry, a picture plane is an image plane located between the “eye point” and the object being viewed and is usually coextensive to the material surface of the work.
Also know, what is a plane in art?
In two-dimensional art, plane refers to a flat or level surface of a material body which can also be imagined in space. Planes of reference are imaginary planes to which the position, direction, and movement of the axes and surfaces of the forms of three-dimensional objects may be related.
Similarly, what is the definition of foreshortening in art? verb Fine Arts. to reduce or distort in order to convey the illusion of three-dimensional space as perceived by the human eye: often done according to the rules of perspective. to abridge, reduce, or contract make shorter.
Regarding this, what is the purpose of the picture plane?
Picture Planes A picture plane is simply whatever you are looking at minus the depth of field. Sort of like if you were to see everything about you through a viewfinder. The reason for this is to help you break the image before you into shapes you can recreate more easily.
What is plane and perspective?
Perspective plane. Also found in: Encyclopedia. the plane or surface on which the objects are delineated, or the picture drawn the plane of projection – distinguished from the ground plane, which is that on which the objects are represented as standing.
You May Like Also
Recommended Reading: Geometry Dash Hack No Root
Properties Of A Plane
Different properties of a plane can be seen based on its position and its interaction with the other planes. Some of the basic properties are mentioned below,
What Is A Plane Figure
A plane figure is defined as a geometric figure that has no thickness. It lies entirely in one plane. It is possible to form a plane figure c with line segments, curves, or a combination of these two, i.e. line segments and curves. Lets have a look at some examples of plane figures in geometry such as circle, rectangle, triangle, square and so on. These are given in the below figure.
Put your understanding of this concept to test by answering a few MCQs. Click Start Quiz to begin!
Select the correct answer and click on the Finish buttonCheck your score and answers at the end of the quiz
Read Also: Who Are Paris Jackson’s Biological Parents
What Is A Plane In Geometry
Geometry is about the observation of shapes, sizes, angles, and dimensions of two-dimensional shapes. These two dimensions of geometrical figures include length and width. The 2D geometries, it is categorized into three types are euclidean geometry, spherical geometry, and hyperbolic geometry. Geometryis the mathematical study of geometrical figures and their properties.
These days geometry is used for computing designs, blueprints, construction, visual and graphic designing, infrastructural development.
Hey! Looking for some great resources suitable for young ones? You’ve come to the right place. Check out our self-paced courses designed for students of grades I-XII.
Start with topics like Python, HTML, ML, and learn to make some games and apps all with the help of our expertly designed content! So students worry no more, because GeeksforGeeks School is now here!
Naming Of Planes In Geometry
Planes in geometry are usually referred to as a single capital letter in italics, for example, in the diagram below, the plane could be named UVW or plane P.
Important Notes
- Any three non-collinear points lie on one and only one plane.
- Two planes always intersect along a line, unless they are parallel.
- A plane is named by three points in that plane that are not on the same line.
Read Also: Define Figure Ground Perception
Points Lines & Planes Lesson & Examples
38 min
- Introduction to points, lines and planes
- 00:00:24 Defining terms: Point, Line, Plane, Collinear, and Coplanar
- 00:08:40
- True or false given the diagram of two planes
- 00:18:57 True or false about collinear and coplanar theory
- 00:21:49 Term Definitions: Line Segments and Rays
- 00:27:33 Name the segments or rays given the illustration
- Practice Problems with Step-by-Step Solutions
- Chapter Tests with Video Solutions
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Definition Of A Plane
In geometry, a plane is a flat surface that extends into infinity. It is also known as a two-dimensional surface. A plane has zero thickness, zero curvature, infinite width, and infinite length. It is actually difficult to imagine a plane in real life all the flat surfaces of a cube or cuboid, flat surface of paper are all real examples of a geometric plane. We can see an example of a plane in which the position of any given point on the plane is determined using an ordered pair of numbers or coordinates. The coordinates show the correct location of the points on the plane.
The figure shown above is a flat surface extending in all directions. So, it is a plane.
Recommended Reading: Elastic Definition Chemistry
How Does It Work
Axiomatic approach is similar to chess in the following aspect.
A chess piece, say a rook, cannot be defined before the whole chess game is defined, since such a phrase as “the rook moves horizontally or vertically, forward or back, through any number of unoccupied squares” makes no sense unless it is already known that “chess is played on a square board of eight rows and eight columns” etc. And conversely, the whole chess game cannot be defined before each piece is defined the properties of the rook are an indispensable part of the rules of the game. No chess without rooks, no rooks outside chess! One must introduce the game, its pieces and their properties in a single combined definition.
Likewise, Euclidean space, its points, lines, planes and their properties are introduced simultaneously in a set of 20 assumptions known as Hilbert’s axioms of Euclidean geometry. The “most basic properties of planes” listed above are roughly the plane-related assumptions , while “further properties” are the first plane-related consequences .
Terms You Need To Know
Point:
A point shows location and has no size or dimension. A point is represented by a dot and is usually named with a letter of choice. In the graphic below, the points are labelled by a nearby letter.
Line:
A line is a set of points extends in two opposite directions without end. A line is one-dimensional and has no width. It is identified by naming two points on the line or by writing a lowercase letter of choice after the line.
The notation, for example, AB , is read as “line AB” and refers to the line that has points A and B.
Plane:
A plane is a flat surface that has no thickness and extends without ending in ALL directions. It is a two-dimensional object. A plane is represented by a parallelogram and may be named by writing an uppercase letter of choice in one of its corners. I will go into detail about what a parallelogram is in future lessons. For now, think of a parallelogram as a “window pane.”For simplicity, you might want to think of a plane as an infinitely large sheet of paper.
The diagram below shows three points, a line, and a plane.
Line Segment:
A line line segment is part of a line having two points, called endpoints. It also has points between the endpoints. A line segment does not have a set of CONTINUOUS points like a line does. Endpoint means that a line has a beginning and an end. The notation for a line segment in a bar over any letter of choice. Say AB has a bar over it, you would read it as “line segment AB.”
Ray:
Angle:
Read Also: How To Find Half Life From Rate Constant
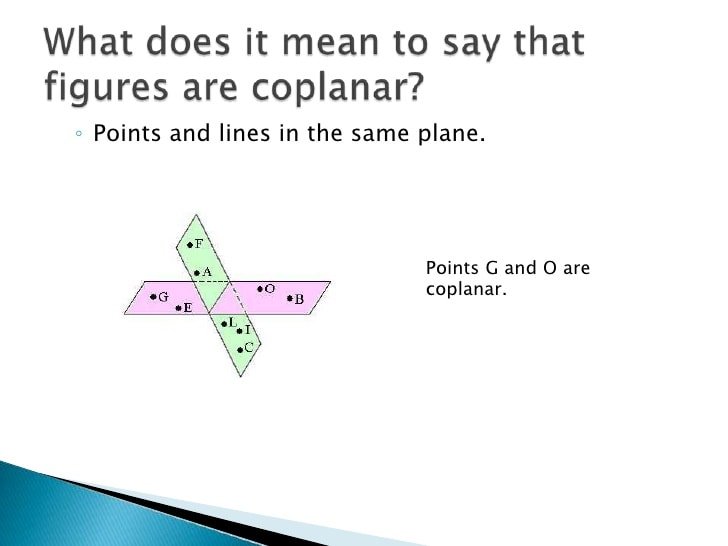
What Does Coplanar Lines Mean In Math
Definition Of Coplanar
linesCoplanar
Moreover, what is the meaning of coplanar lines?
Coplanar lines are lines that lie on the same plane. Picture a giant sheet of paper. Whatever lines are drawn on that sheet of paper will be coplanar because they are lying on the same plane, or the same flat surface.
Secondly, how do you know if a line is coplanar? 2 Answers. Examine both lines in parametric form. If their vectors are parallel then they are certainly coplanar. If their vectors are not parallel, two lines are coplanar if and only iff they intersect otherwise, they are skew.
Beside above, what is an example of coplanar lines?
Coplanar. Points or lines are said to be coplanar if they lie in the same plane. Example 1: The points P , Q , and R lie in the same plane A .
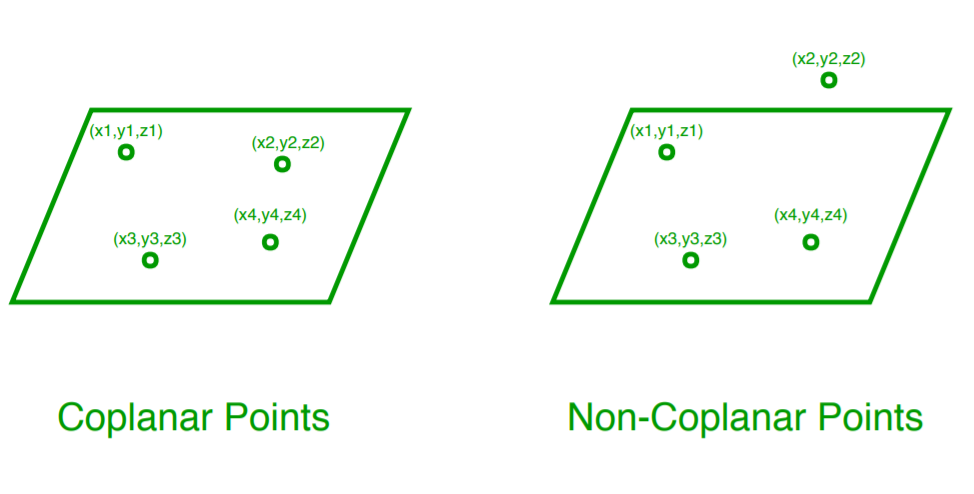
Can 3 points be coplanar?
For example, three points are always coplanar, and if the points are distinct and non-collinear, the plane they determine is unique. However, a set of four or more distinct points will, in general, not lie in a single plane. Two lines in three-dimensional space are coplanar if there is a plane that includes them both.
You May Like Also