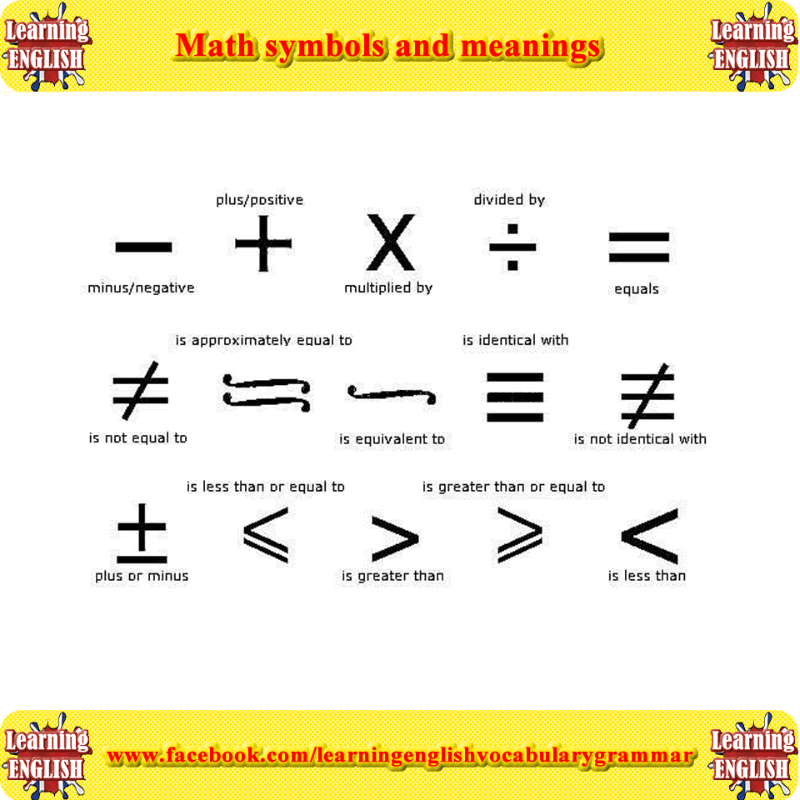
What Does The Word Each Mean In Math
eachperaverage
Of is a powerful word in mathematics, for it can mean a fraction of something, e.g. 4/5 of 25 which commands multiplication or which can imply quotients in some cases such as probability.
Beside above, what does total add or subtract mean math? Adding two numbers means to find their sum . Subtracting one number from another number is to find the difference between them. Multiplication means times . A product is the result of the multiplication of two numbers. Division ‘undoes’ multiplication.
Besides, what words tell you to multiply?
The Basic Operations
Difference Between Mean And Median
Using the example of three people aged 10, 16 and 40, the median age is the value in the middle when the ages are arranged from lowest to highest.
In this case, the median is 16. It is quite different from the mean age of 22 that is calculated by adding the values and dividing by 3.
If there were an even number of ages being considered, such as 10, 16, 20 and 40, then the median would be determined by taking the average of the two numbers in the middle of the group.
In this case, the average of 16 and 20 is 18. The median age is 18, even though that age is not represented in the group. This is why the median is called an approximation for groups of even numbers.
Other Identities Involving The Difference And Complements
There are many set identities that involve the use of the difference and complement operations. Some identities combine other set operations such as the intersection and union. A few of the more important are stated below. For all sets A, and B and D we have:
- A – A =
- DeMorgans Law I: C = AC BC
- DeMorgans Law II: C = AC BC
Read Also: Algebra 1 Eoc Answers 2015
Princeton’s Wordnetrate This Definition:
differencenoun
the quality of being unlike or dissimilar
“there are many differences between jazz and rock”
deviation, divergence, departure, differencenoun
a variation that deviates from the standard or norm
“the deviation from the mean”
dispute, difference, difference of opinion, conflictnoun
a disagreement or argument about something important
“he had a dispute with his wife” “there were irreconcilable differences” “the familiar conflict between Republicans and Democrats”
differencenoun
“the difference in her is amazing” “his support made a real difference”
remainder, differencenoun
the number that remains after subtraction the number that when added to the subtrahend gives the minuend
Description Of The Difference
The subtraction of one number from another can be thought of in many different ways. One model to help with understanding this concept is called the takeaway model of subtraction. In this, the problem 5 – 2 = 3 would be demonstrated by starting with five objects, removing two of them and counting that there were three remaining. In a similar way that we find the difference between two numbers, we can find the difference of two sets.
Also Check: Algebra 1 Age Word Problems
Subtraction Explanation & Examples
Like addition, subtraction is also one of the oldest and the most basic arithmetic operations. The word subtraction is derived from the two words, sub and tract, which mean under or below and to pull or carry away, respectively. Therefore, subtraction means to carry away the lower part.
Subtraction is known to mathematicians for more than 6000 years. German Mathematicians first used the symbol of subtraction as markings on barrels. It is then used as an operational symbol in the 1500s. Later in 1557, it became common when Robert Recorde, a famous Physician and Mathematician, used it in the Whetstone of Witte.
The Meaning Of Root Of Unity
The root of unity refers to the state in which for any integer n, the nth root of a number k is a number that, when multiplied by itself n times, yields the number k. A root of unity in, most simply put, any number which when multiplied by itself any number of times always equals 1. Therefore, an nth root of unity is any number k that satisfies the following equation:
k^n = 1 , where n is a positive integer.
Roots of unity are also sometimes called de Moivre numbers, after the French mathematician Abraham de Moivre. Roots of unity are traditionally used in branches of mathematics like number theory.
When considering real numbers, the only two that fit this definition of roots of unity are the numbers one and negative one . But the concept of the root of unity does not generally appear within such a simple context. Instead, the root of unity becomes a topic for mathematical discussion when dealing with complex numbers, which are those numbers that can be expressed in the form a + bi, where a and b are real numbers and i is the square root of negative one or an imaginary number. In fact, the number i is itself also a root of unity.
Recommended Reading: What Is The Molecular Geometry Of Ccl4
Notation For The Complement
The word “complement” starts with the letter C, and so this is used in the notation. The complement of the set A is written as AC. So we can express the definition of the complement in symbols as: AC = U – A.
Another way that is commonly used to denote the complement of a set involves an apostrophe, and is written as A‘.
Addition Of Large Numbers
To add large numbers, list them in columns and then add only those digits that have the same place value.
Example 2
Find the sum of 5897, 78, 726 and 8569.
Solution:
Note:
- Write the numbers in columns with the thousands, hundreds, tens and units lined up.
- 7 + 8 + 6 + 9 = 30. Thus, the sum of the digits in the units column is 30. So, we place 0 in the units place and carry 3 to the tens place.
- The sum of the digits in the tens column after adding 3 is 27. So, we place 7 in the tens place and carry 2 to the hundreds place.
- The sum of the digits in the hundreds column after adding 2 is 22. So, we place 2 in the hundreds place and carry 2 to the thousdands place.
Read Also: What Is Figure Ground Perception Psychology
Equal Amount Transferred Out Of 2 Variables
Question: Chloe had 18 stickers and Jane had 6 stickers. When they both gave away an equal number of stickers, Chloe had 4 times as many stickers as Jane. How many stickers did they each gave away?Answer: For this question, we will again work backwards. It is always easier to start drawing models where a multiples-relationship exist, i.e., a variable is a multiple of another variable. In this example, Chloe is 4 times of Jane after the transfer out.Step 1: Since the ratio of Chloe’s pens to Jane’s pens after the transfer out is 4:1, we draw 4 boxes to represent the number of units that Chloe had and 1 box to represent the number of units that Jane had.
Step 2: Since an equal amount was transferred out, we add an equal amount back to represent the part that each of them gave away.
Step 3: Next, we label the models with the number of stickers they each had at first.
Step 4: Rearrange the units in Chloe’s bar.
From the model, we can see that after we shift the last unit of Chloe’s bar forward, the remaining 3 unknown but equal units add up to 12.
3 units ———-> 12 stickers
1 unit ———–> 12 stickers / 3 = 4 stickersStep 5: Putting the value of 4 stickers per unit back into the model, we get:
Looking at Jane’s model,
6 stickers – 4 stickers = 2 stickers
Therefore, they each gave away 2 stickers.
Equal Amount Transferred Into 2 Variables
Question: Ken had 14 pens and Ben had 2 pens. When they received an equal number of pens from their teacher, the ratio of Ken’s pens to Ben’s pens became 3:1. How many pens did each of them receive from their teacher?Answer: For this question, we will work backwards. It is always easier to start drawing models where a multiples-relationship exist, i.e., a variable is a multiple of another variable. In this example, Ken is 3 times of Ben after the transfer in.Step 1: Since the ratio of Ken’s pens to Ben’s pens after the transfer in is 3:1, we draw 3 boxes to represent the number of units that Ken had and 1 box to represent the number of units that Ben had.
Step 2: Since an equal amount was transferred in, we mark out an equal amount from both Ken’s and Ben’s model bars to show this amount.
Step 3: Next, we label the models with the number of pens they each had at first.
Step 4: After all information have been put into the model, we can then mark out all the known parts and try to make all the unknown parts equal.
Step 5: From Ken’s bar, we can see that,
2 units + 2 pens + 2 pens + 2 pens ———-> 14 pens
2 units + 6 pens ———-> 14 pens
2 units ———-> 14 pens – 6 pens = 8 pens
1 unit ———-> 8 pens / 2 units = 4 pens
Thus, they reach receive 4 pens from their teacher.
Recommended Reading: Segment And Angle Addition Worksheet
Relative Change And Difference
In any quantitative science, the terms relative change and relative difference are used to compare two quantities while taking into account the “sizes” of the things being compared. The comparison is expressed as a ratio and is a unitlessnumber. By multiplying these ratios by 100 they can be expressed as percentages so the terms percentage change, percent difference, or relative percentage difference are also commonly used. The distinction between “change” and “difference” depends on whether or not one of the quantities being compared is considered a standard or reference or starting value. When this occurs, the term relative change is used and otherwise the term relative difference is preferred. Relative difference is often used as a quantitative indicator of quality assurance and quality control for repeated measurements where the outcomes are expected to be the same. A special case of percent change called percent error occurs in measuring situations where the reference value is the accepted or actual value and the value being compared to it is experimentally determined .
What Is The Difference Between Average And Mean
Average and mean are usually confused with one another as both the mathematical terms are used to explain the set of numbers. Mean can simply be calculated by adding the set of values and divided by the number of quantities. Thus, this is the core definition of what mean is. You can find the tabular column below to learn the difference between the average and mean.
| Difference between Average and Mean | |
|---|---|
|
Average |
Mean |
| Average can simply be defined as the sum of all the numbers divided by the total number of values. | A mean is defined as the mathematical average of the set of two or more data values. |
| Average is usually defined as mean or arithmetic mean. | Mean is simply a method of describing the average of the sample. |
| Average can be calculated for any discrete numbers where it assumes uniform distribution. | It is mainly used in Statistics, and it is applied for any distribution such as geometric, binomial, Poisson distribution, and so on. |
| The arithmetic mean is considered as a form of average. | There are various types of mean. |
| Average is usually used in conversations in general day to day English. | Mean is used in a more technical and mathematical sense. |
| The average is capable of giving us the median and the mode. | Mean, on the other hand, cannot give us the median or mode. |
Read Also: Ccl4 Dot Structure
Subtraction Of Large Numbers
To subtract large numbers, list them in columns and then subtract only those digits that have the same place value.
Example 4
Find the difference between 7064 and 489.
Solution:
Note:
- Use the equals addition method or the .
- Line up the thousands, hundreds, tens and units place values for the two numbers when placing the smaller number below the larger number as shown above.
What Does Math Literacy Mean
The process of developing literacy skills is fairly well known. First we learn sounds, then letters, then how the letters and sounds make wordsand along the way we learn what it all means and how to make sense of our written language.
Literacy skills are very important in school : the stronger that students reading comprehension skills are, the greater their chances of achieving academic success.
So, what does math literacy mean?
- Math literacy means having the ability to problem-solve, reason and analyze information.
- Math literacy is the second key step for all students, beyond language literacy.
- It is the ability to use numbers to help solve real-world problems.
- It is also the ability to understand the language of math .
- Math literacy helps helps students to decipher what a question is actually asking by understanding the terminology.
Read Also: Geometry Segment Addition Postulate Worksheet
The Constant Difference Concept
The Constant Difference Concept is derived from the
Comparison Concept . This concept is applicable when the problems deal with an equal quantity being transferred in or transferred out of the two variables concerned. This leaves the two variables with an equal increase or decrease in value. The unique feature in this concept lies in the fact that after the transfer in or transfer out of quantities, the difference between the two variables remains unchanged, hence the name “Constant Difference” Concept.
To illustrate this concept, take a look at the following problems.
What Is The Difference Of Two Sets In Set Theory
- M.S., Mathematics, Purdue University
- B.A., Mathematics, Physics, and Chemistry, Anderson University
The difference of two sets, written A – B is the set of all elements of A that are not elements of B. The difference operation, along with union and intersection, is an important and fundamental set theory operation.
Read Also: Definition Of Abiotic In Biology
Any Tips For Improving Math Literacy Skills
- Its never too late to build math skills or review the basic concepts. The better the basic conceptsadding, subtracting, division, multiplication and fractionsare understood, the easier that math becomes.
- The earlier that students repair their math skill gaps, the greater the chance that they can become math literate.
- Students need to stop thinking of math as something that they will only use in the classroom.
- Math is everywhere and it IS used in everyday life from cooking, to fitness, home décor, landscaping, nursing, driving, even art. What is computer science? Math. What is creativity? Math.
- Often, a lack of confidence and/or motivation gets in the way of students achieving math literacy.
- It is very important for students to have positive experiences with math from an early age with many opportunities to achieve success. Feeling capable and competent goes a long way toward achieving math literacy.
- Some students dont see the value of becoming math literate, asking When am I ever going to use this? If students are shown real-world examples of how math is used in our daily lives, this can help to motivate them to make the effort needed to become math literate.
6 Easy Ways To Make Math Fun For Kids
While some of us naturally find math fun, others may be looking for ways to spice up thje subject at home. Here are a few ideas!
What Is A Mean Difference
The mean difference, or difference in means, measures the absolute difference between the mean value in two different groups. In clinical trials, it gives you an idea of how much difference there is between the averages of the experimental group and control groups.
Note: Although a lot of authors use the term mean difference, it makes more intuitive sense to say difference between means. Thats because you arent actually calculating any means Youll already have two or more means, and all you need to do is find a difference between them. In other words, youre finding a difference between means and not a mean of differences.
Also Check: What Is K Physics
What Are The Common Challenges To Developing Math Literacy
- Students typically struggle with pattern recognition and the ability to transfer skills.
- Math requires abstract thinking and sometimes that is a difficult transition for students.
- Students also find it a challenge to interpret word problemsfiguring out exactly what the problem is asking them to do, and the steps that they need to complete to find the answer.
Difference Between Average And Mean
To understand the difference between average and mean, one must be aware of what separates one from the other. Average and mean are used interchangeably. In Statistics, instead of the term average, the term mean is used. Average can simply be defined as a quantity or a rate which usually fall under the centre of the data. The average is quite similar to mean but also has its key differences from mean as well. If one can understand the arithmetic mean and range, it can be incredibly helpful in understanding and solving math topics.
Read Also: Practice 2-4 Reasoning In Algebra Answers
The Mathematical Definition Of Unity
- Ph.D., Business Administration, Richard Ivey School of Business
- M.A., Economics, University of Rochester
- B.A., Economics and Political Science, University of Western Ontario
The word unity carries many meanings in the English language, but it is perhaps best known for its most simple and straightforward definition, which is “the state of being one oneness.” While the word carries its own unique meaning in the field of mathematics, the unique use does not stray too far, at least symbolically, from this definition. In fact, in mathematics, unity is simply a synonym for the number “one” , the integer between the integers zero and two .
The number one represents a single entity and it is our unit of counting. It is the first non-zero number of our natural numbers, which are those numbers used for counting and ordering, and the first of our positive integers or whole numbers. The number 1 is also the first odd number of the natural numbers.
The number one actually goes by several names, unity being just one of them. The number 1 is also known as unit, identity, and multiplicative identity.