Introduction To 3 Dimensional Geometry

What Does Three Dimensional Geometry Contain

The field of three-dimensional geometry is massive. Several essential topics fall under this category. So, you need to learn them by heart to top your exams. Coordinate of a point in space is a primary topic. Students may also learn about the angle between two intersecting lines, equation of line and plane. They may also learn about the intersection of line and plane. Apart from this, teachers may also cover direction cosine and direction ratio. Finally, skew lines and the smallest distance between two lines is also a part of 3D Geometry.

The Properties Of Three

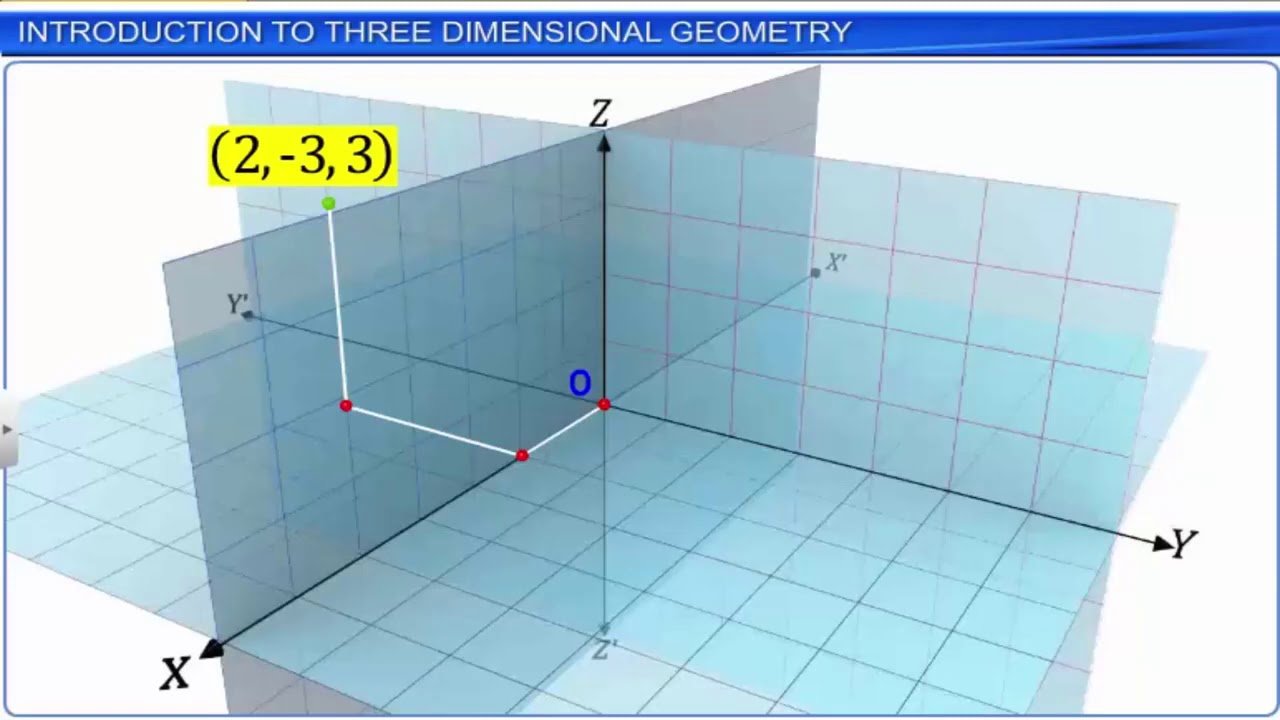
• A point is represented by an ordered triple that consists of three numbers, an x-coordinate, a y-coordinate, a z-coordinate.

• In the two-dimensional xy-plane, these coordinates indicate the signed distance along the coordinate axes,

• The x-axis, y-axis, and z-axis, respectively, originate from the origin, denoted by O, which has coordinates .

Mcq Questions For Class 11 Introduction To Three

Students can refer to MCQ Questions for Class 11 Introduction to Three-Dimensional Geometry provided below. You should solve these questions and compare your answers with the solutions provided below by our teachers. The MCQs for Grade 11 Introduction to Three-Dimensional Geometry have been updated based on the latest syllabus and examination guidelines issued by CBSE, NCERT and KVS.

Don’t Miss: 6 Major Branches Of Chemistry

A Few Points On Chapter 12 Introduction To Three Dimensional Geometry

• In three dimensional geometry, a cartesian coordinate system consists of three mutually perpendicular lines namely x, y and z-axes. They are measured in the same unit of length.
• The three planes XY-plane, YZ-plane and ZX-plane are determined by the pair of axes called the axes of the coordinate planes.
• The three coordinate planes divide the space into eight parts known as octants.
• The coordinates of a point P in three-dimensional geometry is written in the form of an ordered triplet. Here x, y and z are the distances from the YZ, ZX and XY-planes.
• Any point on the x-axis is represented as Any point on the y-axis is represented as Any point on the z-axis is represented as .
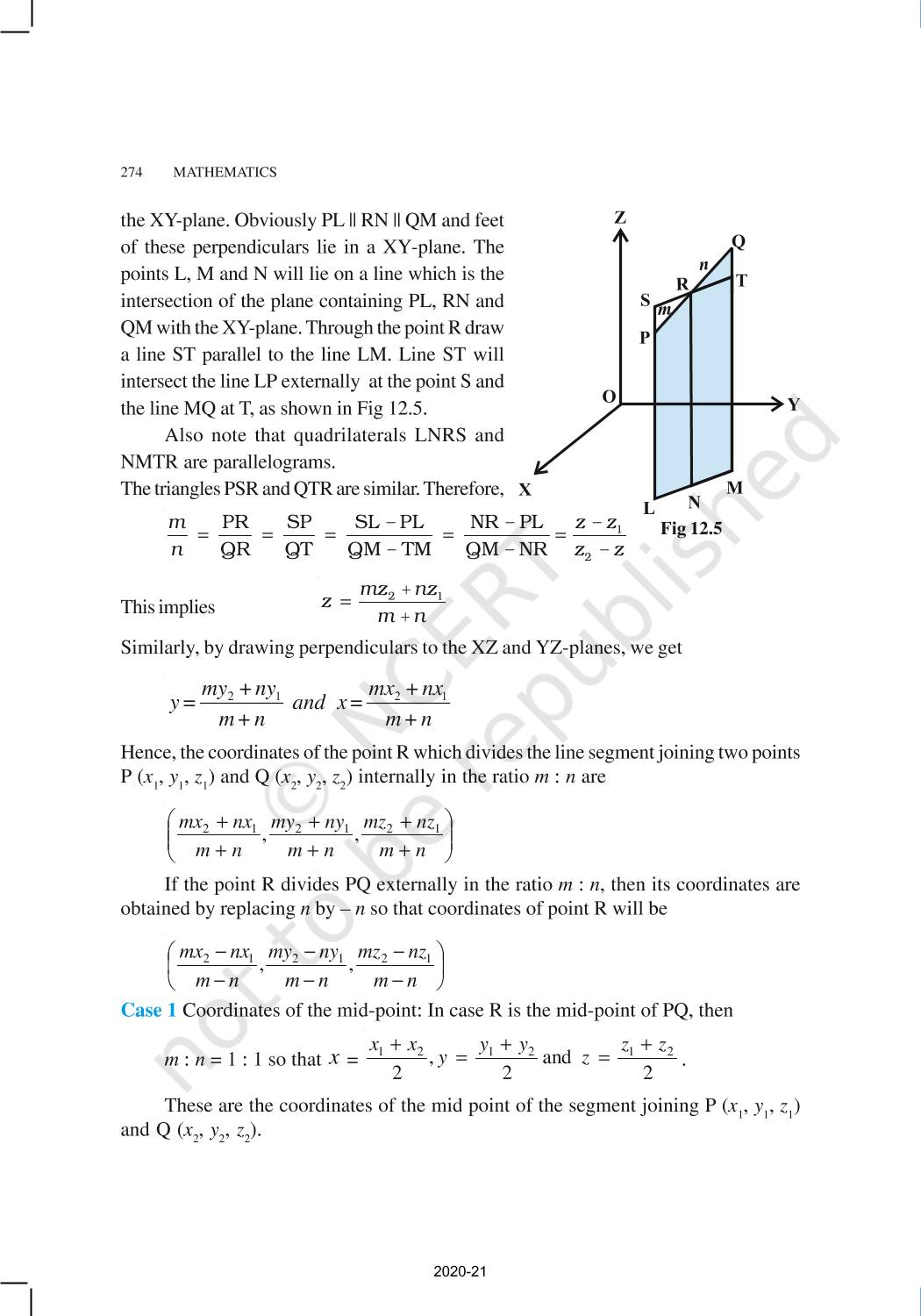
• The coordinates of the point R divide the line segment joining two points P and Q internally and externally in the ratio m:n.

Subject experts at BYJUS who have prepared the NCERT Solutions for Class 11 Maths have years of understanding about the question paper setting and types of questions that would appear in the second term exam. These solutions provide alternative methods and explanations to solve problems that make the students feel confident while facing the term II exam. Also, solving many complicated problems enhances the Mathematical ability of the students. The solutions cover all the necessary questions, which a student must and should have mastered to appear for the second term exam.

Class 11 Introduction Of 3d Worksheet Pdf

CBSE Class 11 Mathematics Worksheet – Introduction To 3-Dimensional Geometry – Practice worksheets for CBSE students. Prepared by teachers of the best CBSE schools in India.

Students must free download and practice these worksheets to gain more marks in exams. CBSE Class 11 Mathematics Worksheet – Introduction To 3-Dimensional Geometry

Recommended Reading: Geometry Basics Segment Addition Postulate Worksheet Answer Key

Representation Of A Plane In 3d Geometry

The equation of a plane in a cartesian coordinate system can be computed through different methods based on the available inputs values about the plane. The following are the four different expressions for the equation of a plane.

• Normal Form: Equation of a plane at a perpendicular distance d from the origin and having a unit normal vector \ is \ = d.
• Perpendicular to a given Line and through a Point: The equation of a plane perpendicular to a given vector \, and passing through a point \ is \. \overrightarrow N = 0\)
• Through three Non Collinear Lines: The equation of a plane passing through three non collinear points \, \, and \, is \ = 0\).
• Intersection of Two Planes: The equation of a plane passing through the intersection of two planes \, and \, is \ = d_1 + d_2\).

Related Topics

Cbse Class 11 Maths Notes Chapter 12 Introduction To Three Dimensional Geometry

Introduction To Three Dimensional Geometry Class 11 Notes Chapter 12

Coordinate AxesIn three dimensions, the coordinate axes of a rectangular cartesian coordinate system are three mutually perpendicular lines. These axes are called the X, Y and Z axes.

Coordinate PlanesThe three planes determined by the pair of axes are the coordinate planes. These planes are called XY, YZ and ZX plane and they divide the space into eight regions known as octants.

Introduction To 3d Geometry Class 11 Notes Chapter 12

Coordinates of a Point in SpaceThe coordinates of a point in the space are the perpendicular distances from P on three mutually perpendicular coordinate planes YZ, ZX, and XY respectively. The coordinates of a point P are written in the form of triplet like .The coordinates of any point on

• X-axis is of the form
• Y-axis is of the form
• Z-axis is of the form
• XY-plane are of the form
• YZ-plane is of the form
• ZX-plane are of the form

Distance FormulaThe distance between two points P and Q is given by

The distance of a point P from the origin O is given byOP = \

3d Geometry Class 11 Notes Chapter 12

Section FormulaThe coordinates of the point R which divides the line segment joining two points P and Q internally or externally in the ratio m : n are given by

The coordinates of the mid-point of the line segment joining two points P and Q are

The coordinates of the centroid of the triangle, whose vertices are , and are

3d Geometry Class 11 Notes Pdf Chapter 12

Also Check: Are Michael Jackson’s Kids Biologically His

Class 11 Introduction To Three Dimensional Geometry

In Class 11 Maths Chapter 12 Introduction to Three Dimensional Geometry Notes, we have given all the important concepts related to 3D geometry explained in the chapter. The topics here include:

• Coordinate axes
• Coordinate of point in space
• Distance between two points

Also check: Equation Of A Line In Three Dimensions

Coordinate System In 3d Geometry

In 3-dimensional coordinate geometry, a coordinate system refers to the process of identifying the position or location of a point in the coordinate plane. To understand more about coordinate planes and systems, refer to the coordinate geometry lesson which covers all the basic concepts, theorems, and formulas related to coordinate or analytic geometry.

Don’t Miss: Density Vs Concentration Human Geography

Components Of A Vector

If we consider a Cartesian coordinate system, any vector can be defined in terms of 3 components. We can define the notation of any vector as:

v = |x| \ + |y| \ + |z| \

Where \, \, and \ are the unit vectors along the x, y and z-axes respectively, and |x|, |y|, and |z| denote the length of the components of the vector along these axes respectively. The magnitude of a vector V, is |x| \ + |y| \ + |z| \ can be denoted as |V|, where:

|V| =

Example: Calculate the x, y, and z components of the vector u = 3\ + 4\ + 5\ as well as the magnitude of the vector.

Solution: In the above problem, we have |x| = 3, |y| = 4, and |z| = 5

x-component = 3, y-component = 4, z-component = 5

|u| = = 52

How Do 3d Coordinates Work

For most parts, the formulation of three-dimensional geometry is known as the origin. It may also be known as a basis that contains three common perpendicular vectors. With these vectors at hand, it becomes a cakewalk to understand the three coordinate axes. The x-coordinate, y-coordinate and z-coordinate are the three different coordinate axes to know about. These are also referred to as the applicate axis, abscissa and ordinate axes. With more in-depth learning, you will be able to acquire more relevant information on time.

Don’t Miss: Algebra Nation Section 3 Answers Test Yourself

Mathematics Introduction Of 3d Worksheets For Class 11

We have provided chapter-wise worksheets for class 11 Mathematics Introduction Of 3D which the students can download in Pdf format for free. This is the best collection of Mathematics Introduction Of 3D standard 11th worksheets with important questions and answers for each grade 11th Mathematics Introduction Of 3D chapter so that the students are able to properly practice and gain more marks in Class 11 Mathematics Introduction Of 3D class tests and exams.

Class 11 Introduction To Three

See below free multiple choice questions for Class 11 Introduction to Three-Dimensional Geometry. By practicing these MCQ Questions for Class 11 Mathematics you will be able to revise the entire course and also test your understanding

MCQ Questions for Class 11 Introduction to Three-Dimensional Geometry

Question. The ratio in which the line joining the points and divides the segment joining the points and is 1 : 2

Question. The coordinates of three vertices of a rectangle are , and , the 4th vertex is

Question. y-axis divides the segment joining points and in the ratio 1 : 3

Question. Let AB be divided internally and externally at P and Qin the same ratio. Then, AP, ABand AQare is AP

Question. The points and are vertices of an isosceles triangle a right angled triangle None of these

Question. x-axis divides line segment joining points and in the ratio 1: 2

Question. Let P and Q be points in the line joining A and B such that AP = PQ = QB. Then, the mid-point of PQ is

Question. If the points , and are vertices of an equilateral triangle, then the value of k will be 1

Question. The pointswhich trisect the line segment joining the pointsand are , , , ,

Question. The points , , and are the vertices of a parallelogram

Question. If A, B , C are the vertices of a ABC, then the locus of centroid of triangle is x2 + y2 -2x 4y + 1= 0 -2x 4y + 1= 0 x2 + y2 -2x 4y + 3= 0 None of the above

Question. The area of the triangle with vertices at the point ,, is 0

You May Like: Geometry Textbook Mcdougal Littell Answers

Best Book For Three Dimensions Geometry :

Maths NCERT Books are one of the most important study material as this book covers all the topics. Start from NCERT book, the example given in NCERT is simple and lucid. Most of the important concepts and theory you will understand by simply solving those given example. And also solve all problems of NCERT. If you do this, your basic level of preparation will be completed.

Then you can refer to the books Vectors & 3D Geometry by Amit M. Agarwal, Cengage Mathematics Vectors & 3D Geometry or RD Sharma. 3D Geometry explained very beautifully in the book Arihant Algebra and there are lots of questions with crystal clear concepts. But again the choice of reference book depends on you, find the book that best suits you the best depending on how well you are clear with the concepts and the difficulty of the questions you require. Rather than referring all the books just stick to one good book but for practicing more problem you can refer to other books.

Why Is Three Dimensional Geometry Important

In most board exams, three-dimensional geometry plays a crucial role. Since it is highly scoring, most students who find the remaining questions challenging to answer can find their solace in this one. Also, three-dimensional geometry is relatively simple to understand. That is why those who pay attention from the start have a broad scope of topping their math papers shortly.

Don’t Miss: The Shape Of Ccl4 Is

Rectangular Coordinate System In Space

The coordinate system defines the position of a vector. In the rectangular coordinate in space, we refer to the three-dimensional space. To demonstrate the position of a vector, mark a point as the origin, represented by the point O. The distance of any vector is now measured from this standard point.

Let O be any point in space called origin and XOX, YOY and ZOZ be three lines perpendicular to each other and these three lines denote the coordinate X, Y, and Z-axis. The planes XY, YZ, and ZX are called the coordinate planes in space.

Coordinates Of A Point In Space

Consider a point P in space. The position of the point P is given by the coordinates where x, y, z denotes the perpendicular distance from YZ-plane, ZX-plane, and XY-plane respectively. If the vectors i, j, k are assumed to be the unit vectors along OX, OY, OZ respectively, then the position vector of point P is xi + yj + zk or simply .

If O is the origin and P is any point with coordinates from the origin then the distance vector OP by the distance formula is given by OP = \

You May Like: Paris Jackson’s Biological Father

Activity 2 Polygon And Volume Power

Examine geometry around your home. Find examples of two dimensional geometry: triangles, rectangles and pentagons anywhere you can. Then, find examples of three dimensional geometry: spheres, pyramids, cylinders and cubes.

Look at the floor tile, the design of a door knob or even your soccer ball. Photograph or sketch what you find, then copy them, label them and paste the shapes in your journal. Think about how to fold a 3-dimensional shape from a flat piece of paper. Is it even possible? Start with a square shape and draw all six sides on a flat sheet of construction paper. Cut and fold your design into a cube. Then work with a triangle to make a pyramid. Finally, be brave! Try to draw and fold more complex shapes into regular solids.

Ml Aggarwal Introduction To 3

ML Aggarwal Introduction to 3-D Geometry ISC Class-11 Maths Understanding Solutions Chapter-2. Step by step Solutions of ML Aggarwal ISC Class-11 Mathematics with Exe-2.1, Exe-2.2, Exe-2.3, and Chapter Test Questions. Visit official Website CISCE for detail information about ISC Board Class-11 Mathematics.

You May Like: Lewis Structures And Molecular Geometry Lab

Magnitude Of A Vector

The magnitude of a vector is a measure of how long a vector is. Consider a vector whose tail is given by T and whose head is given by H. If we define this vector as V, then the magnitude of the vector is denoted as |V|, where:

|V| =

Example: Calculate the magnitude of a vector whose tail is given by , and whose head is given by

Solution: In the given example, we have:

x1 = 1, x2 = 4, y1 = 2, y2 = 5, z1 = 3, z2 = 6

|V| =

|V| = 33 units

Example: Calculate the magnitude of a vector whose tail is , and whose head is

Solution: In the given example, we have:

x1 = -1, x2 = 4, y1 = -4, y2 = 7, z1 = 3, z2 = -2

|V| =

So, |V| = )2+)2+-3)2}

|V| = 171 = 319 units

A unit vector is any vector that has a magnitude of 1.

Ncert Solutions For Class 11 Maths Chapter 12 Free Pdf Download

NCERT Solutions for Class 11 Maths Chapter 12 Introduction To Three Dimensional Geometry empowers the students to solve the problems in a dynamic way of consuming less time. The NCERT Solutions are written by highly experienced teachers according to the latest update on term-wise CBSE Syllabus 2021-22 making the clarification of every problem straightforward and precise. The students can refer to this Chapters NCERT Solutions for Class 11 Maths PDF from the link provided below for optimum term II exam preparations.

Don’t Miss: Steve Harvey Oldest Son

I Mathematics Introduction Of 3d Worksheets For Class 11 As Per Cbse Ncert Pattern

Parents and students are welcome to download as many worksheets as they want as we have provided all free. As you can see we have covered all topics which are there in your Class 11 Mathematics Introduction of 3D book designed as per CBSE, NCERT and KVS syllabus and examination pattern. These test papers have been used in various schools and have helped students to practice and improve their grades in school and have also helped them to appear in other school level exams. You can take printout of these chapter wise test sheets having questions relating to each topic and practice them daily so that you can thoroughly understand each concept and get better marks. As Mathematics Introduction of 3D for Class 11 is a very scoring subject, if you download and do these questions and answers on daily basis, this will help you to become master in this subject.

Benefits of Free Introduction to Three Dimensional Geometry Class 11 Worksheets

Distance Formula In 3d

In 2D coordinate geometry, the distance between two pints $P$ & $Q$ is given by

$PQ = \sqrt$ similar in a 3D coordinate system, the distance between two points $A$ and $B$ is given by $AB = \sqrt$

Note: Distance of a point $P$ from the origin $O$ is

$OP = \sqrt$

$OP = \sqrt$

Illustrated Example

Example1: Find the distance between the points $A$ & $B$.

Sol.

Required Distance

$AB = \sqrt $

$AB = \sqrt = \sqrt = \sqrt49 = 7\text$

Don’t Miss: Ccl4 Electron Pair Geometry

Class 11 Maths Ncert Solutions Miscellaneous Questions

Miscellaneous Exercise Class 11 Maths Question 1:Ans:Miscellaneous Exercise Class 11 Maths Question 2:Ans:Miscellaneous Exercise Class 11 Maths Question 3:Ans:Miscellaneous Exercise Class 11 Maths Miscellaneous Exercise Class 11 Maths Question 4:Ans:Miscellaneous Exercise Class 11 Maths Question 5:Ans:Miscellaneous Exercise Class 11 Maths Question 6:Ans:

Exercise 12.1

For any given point, the sign of its coordinates determines the octant in which it will lie.

Now, from the following table it can be easily determined in which coordinates the point lies.

Q.1: A point is lying on y axis. What are its x coordinates and z coordinates?

Q.2: A point is lying on YZ plane. What are its x coordinates?

Q.3: In which of the octant the following points lie:

, , , , , , ,

Q.4: Answer the following questions:

. What is the name of a plane determined by the Z-axis and the Y-axis when taken together?

. What is the general form of coordinates of points in the XZ-plane?

. Coordinate plane divides the space into how many octants?

Exercise: 12.2

Q.1: Find the distance between two points whose coordinates are given below:

. and

. and

. and

. and

Q.2: Show that the points , and are collinear.

Q.3: Prove the following statements:

. , and are the vertices of a right angled triangle.

. , and are the vertices of an isosceles triangle.

. , , and are the vertices of a parallelogram.

Q.4: Find the equation of the set of points P which are equidistant from point A and point B .

Exercise 12.3