Know How To Use The Pythagorean Theorem
Many math problems dealing with the area of a triangle arent just about finding the area itself but rather finding a missing side or length , too. In these cases you’ll need to know more than just how to find the area of a triangle you’ll have to know the Pythagorean theorem.
As mentioned above, the Pythagorean theorem is a formula used to find the lengths of the sides of a right triangle.
Here is the theorem once again:
$a^2+b^2=c^2$
In this, a is the length of one short side, b is the length of the other short side, and c is the length of the hypotenuse . Youll need to use the Pythagorean theorem if youre looking for both the height and area of an isosceles or equilateral triangle.
Units For Measuring Area
We measure area using squares. We use different sizes of squares depending on how big or small an area is.
| Example |
| Dont forget the wee 2 |
| We write square sizes using a small 2 next to the unit.We write mm2, cm2, m2 , km2, cm2We can say 63 millimeters squared or 63 square millimeters |
We could use small squares to measure large areas. The only problem with this is that we would end up having to use very big numbers. For example, a field might be measured at 5,000,000,000 square millimeters when 5,000 square meters would be a much easier size to say, write, and visualize.
You will probably hear more units for measuring area square inches, square feet, square yards, square miles, acres, hectares are all units used for measuring area.
Explanation Of The Area Of A Circle Formula
Take a circle and divide it into equally sized sectors and rearrange these as shown below. Notice how, as the sectors become smaller, the shape becomes more like a rectangle. Note: There is no limit to how small these sectors could be and to how closely they could resemble a rectangle when arranged.
Assuming we know that the circumference of a circle is equal to 2r we can add dimensions to the rectangle as shown below. Using the area of a rectangle area formula, area = width x height we can see how our circle, re-configured as a rectangle, can be shown to have an area that approximates to r x r or r2
Circle Sectors Rearranged
Circle Sectors Rearranged Starting to Look Like a Rectangle
You May Like: Paris Jackson’s Mother
What Is An Average In Mathematics
In mathematics, an average is the sum of a group of numbers divided by the quantity of items in the group.
So if you have three people holding books, you can find the average number of books they are holding like this: Martin is holding 5 books, Mack is holding 3 books, and Maria is holding 4 books. Together, 12 books are being held by 3 people. So, 12 books ÷ 3 people = an average of 4 books each.
Area Of A Triangular Room
If you have a really original-looking room in the shape of a triangle, and you want to lay carpet in that room, you would use the formula for finding the area of a triangle. You’d first need to measure the base of the triangle. Suppose you find that the base is 10 feet. You’d measure the height of the triangle from the base to the top of the triangle’s point. If the height of your triangular room’s floor is 8 feet, you’d use the formula as follows:
- A = ½ x B x H
- A = ½ x 10 feet x 8 feet
- A = ½ x 80 feet
- A = 40 square feet
So, you’d need a whopping 40 square feet of carpet to cover the floor of that room. Make sure you have enough credit remaining on your card before heading to the home-improvement or carpeting store.
Recommended Reading: Age Word Problems Algebra
What Is The Meaning Of Area
The word ‘area’ means a vacant surface. The area of a shape is calculated with the help of its length and width. Length is unidimensional and measured in units such as feet , yards , inches , etc. However, the area of a shape is a two-dimensional quantity. Hence, it is measured in square units like square inches or , square feet or , square yard or , etc. Most of the objects or shapes have edges and corners. The length and width of these edges are considered while calculating the area of a specific shape.
What Is The Area Of A Square
The area of a square is a number of square units needed to completely fill a square. To understand that definition, let’s have a look at this picture of a chessboard:
The board has a squared shape, with its side divided into eight parts, in total it consists of 64 small squares. Assume that one small square has a side length equal to 1 in. The area of such square may be understood as the amount of paint necessary to cover the surface. So, from the formula for the area of a square, we know that area = a² = 1 in², and it’s our unit of area in chessboard case . The area of 2×2 piece of the chessboard is then equal to 4 squares – so it’s 4 in² and we need to use 4 times more “paint”. Full chessboard area equals 84 in²: 8 in * 8 in from the formula or it’s just 64 small squares with 1 in² area – so we need 64 times more “paint” than for one single square.
You may also be interested to check out the area of the largest square in a circle!
You May Like: Theory Of Everything Geometry
Reflection In The Coordinate Plane
The reflection in the coordinate plane may be in reference to X-axis and Y-axis.
Reflection of a Point in the x-axis
In the case of reflection over the x-axis, the point is reflected across the x-axis. The x-coordinates remain the same and the y-coordinates will be transformed into their opposite sign.The reflection of the point across the x-axis is
Reflection of a Point in the y-axis
In the case of reflection over the y-axis, the point is reflected across the y-axis. The y-coordinates remain the same and the x-coordinates will be transformed into their opposite sign.The reflection of the point across the x-axis is
Reflection in a point
A reflection point happens when a figure is built around a solitary point known as the mark of reflection or focus of the figure. For each point in the figure, another point is seen as straightforwardly inverse to it on the opposite side. Under the mark of reflection, the figure doesnt change its size and shape.
Reflection in Origin
In a plane, we can use any point as the point of reflection and the most commonly used point is the origin.The point of reflection in origin , the image of the point is .
Areas Of Simple Quadrilaterals: Squares And Rectangles And Parallelograms
The simplest area calculations are for squares and rectangles.
To find the area of a rectangle, multiply its height by its width.
Area of a rectangle = height × width
For a square you only need to find the length of one of the sides and then multiply this by itself to find the area. This is the same as saying length2 or length squared.
It is good practice to check that a shape is actually a square by measuring two sides. For example, the wall of a room may look like a square but when you measure it you find it is actually a rectangle.
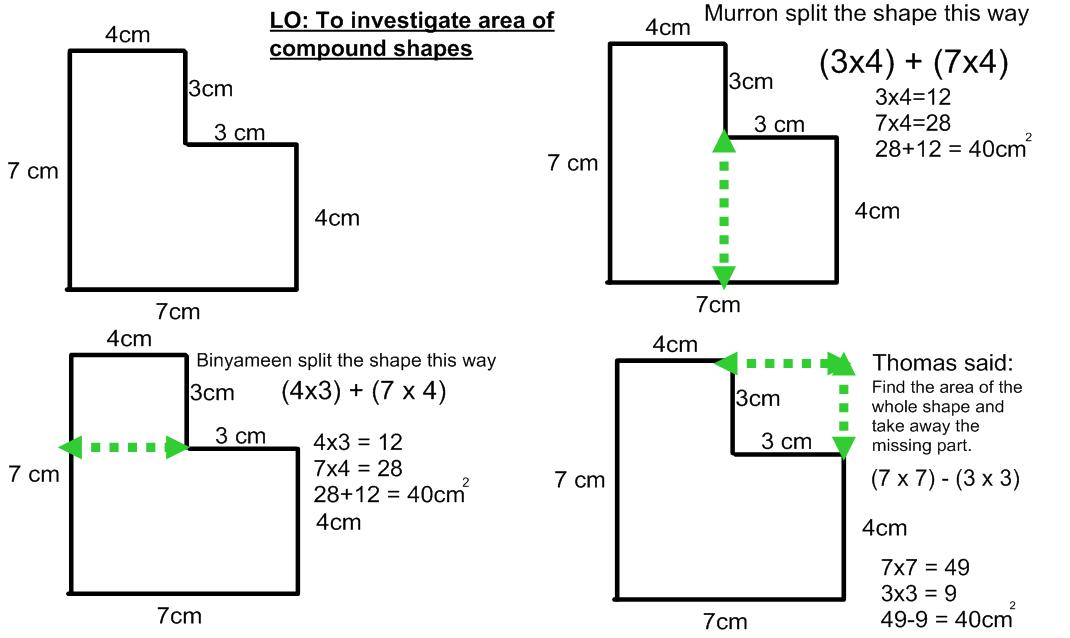
Often, in real life, shapes can be more complex. For example, imagine you want to find the area of a floor, so that you can order the right amount of carpet.
A typical floor-plan of a room may not consist of a simple rectangle or square:
In this example, and other examples like it, the trick is to split the shape into several rectangles . It doesnt matter how you split the shape – any of the three solutions will result in the same answer.
Solution 1 and 2 require that you make two shapes and add their areas together to find the total area.
For solution 3 you make a larger shape and subtract the smaller shape from it to find the area.
Another common problem is to the find the area of a border a shape within another shape.
This example shows a path around a field the path is 2m wide.
Again, there are several ways to work out the area of the path in this example.
The area of the path is 88m2.
Read Also: Blanket Jackson Real Parents
When In Doubt Review What Youve Learned
Theres no shame in refreshing your memory or getting help! If youre struggling to understand how to find the area of a triangle or when and how to use the Pythagorean theorem, I strongly recommend watching some math tutorial videos.
Heres an example of a video I found particularly helpful while writing this article:
You can also check out Khan Academy, a free website that offers a bunch of videos, lessons, and practice problems for an array of math subjects, including triangles and area.
Finally, read our SAT Math/ACT Math triangle guides to learn more about triangles in general.
What Is A Trapezoid
A trapezoid is a quadrilateral with one pair of parallel sides. So, this four-sided polygon is a plane figure and a closed shape. It has four line segments and four interior angles. The parallel sides are the trapezoid’s two bases the other two sides are its legs.
Usually the trapezoid is presented with the longer parallel side — the base — horizontal. A perpendicular line from the base to the other parallel side will give you the trapezoid’s height or altitude.
You May Like: Punchline Bridge To Algebra Answer Key Page 115
How To Use The Area Of A Square Calculator
Let’s give the area of a square calculator a try!
Calculating Area Using The Grid Method

When a shape is drawn on a scaled grid you can find the area by counting the number of grid squares inside the shape.
In this example there are 10 grid squares inside the rectangle.
In order to find an area value using the grid method, we need to know the size that a grid square represents.
This example uses centimetres, but the same method applies for any unit of length or distance. You could, for example be using inches, metres, miles, feet etc.
In this example each grid square has a width of 1cm and a height of 1cm. In other words each grid square is one ‘square centimetre’.
Count the grid squares inside the large square to find its area..
There are 16 small squares so the area of the large square is 16 square centimetres.
In mathematics we abbreviate ‘square centimetres’ to cm2. The 2 means squared.
Each grid square is 1cm2.
The area of the large square is 16cm2.
Counting squares on a grid to find the area works for all shapes as long as the grid sizes are known. However, this method becomes more challenging when shapes do not fit the grid exactly or when you need to count fractions of grid squares.
In this example the square does not fit exactly onto the grid.
We can still calculate the area by counting grid squares.
- There are 25 full grid squares .
- 10 half grid squares 10 half squares is the same as 5 full squares.
- There is also 1 quarter square .
- Add the whole squares and fractions together: 25 + 5 + 0.25 = 30.25.
You can also write this as 30¼cm2.
Don’t Miss: Define Movement In Geography
Areas Determined Using Calculus
The development of integral calculus in the late 17th century provided tools that could subsequently be used for computing more complicated areas, such as the area of an ellipse and the surface areas of various curved three-dimensional objects.
- ) | }\sum _^}
where when i=n-1, then i+1 is expressed as modulusn and so refers to 0.
Rectangles
The most basic area formula is the formula for the area of a rectangle. Given a rectangle with length l and width w, the formula for the area is:
- A = lw .
That is, the area of the rectangle is the length multiplied by the width. As a special case, as l = w in the case of a square, the area of a square with side length s is given by the formula:
- A = s2 .
The formula for the area of a rectangle follows directly from the basic properties of area, and is sometimes taken as a definition or axiom. On the other hand, if geometry is developed before arithmetic, this formula can be used to define multiplication of real numbers.
Dissection, parallelograms, and triangles
Most other simple formulas for area follow from the method of dissection.This involves cutting a shape into pieces, whose areas must sum to the area of the original shape.
For an example, any parallelogram can be subdivided into a trapezoid and a right triangle, as shown in figure to the left. If the triangle is moved to the other side of the trapezoid, then the resulting figure is a rectangle. It follows that the area of the parallelogram is the same as the area of the rectangle:
How To Calculate Area
Let us see how to calculate the area of a shape with the help of a grid. The area of any shape is the number of unit squares that can fit into it. The grid is made up of many squares of sides 1 unit by 1 unit. The area of each of these squares is 1 square unit. Hence, each square is known as a unit square. Look at the figure shown below. Let us find the area of the shape drawn in the grid.
The area of this shape is the number of shaded unit squares.
Thus, the area of the shape = 9 square units. Now, let us look at another example. When the shape does not occupy a complete unit square, we can approximate and find its value. If it occupies about 1/2 of the unit square, we can combine two such halves to form an area of 1 square unit. Observe the figure given below.
Here, the area occupied by the shape = 4 full squares and 8 half squares. Together this forms an area of 8 square units. If the shaded region is less than 1/2, we can omit those parts. For regular shapes, we have certain formulas to calculate their area. Note that this is only an approximate value.
Also Check: Algebra 1 Eoc Practice Packet
Keys To Being A Good Math Student
Learning Math In School
Read Also: Cosine In Physics
How To Find The Area Of A Shape
Flat shapes have two dimensions:
A square, for instance, has a width equal to its length because all side lengths are the same. An ellipse has width and length, too.
We can easily see how the square could be divided up into small, square units like on a coordinate plane. You cannot easily see how an ellipse could be made up of little squares, but it can be.
Since it has width and length, it covers a space, and that space, even with the curving sides of the ellipse, can be divided up into square units:
Counting the square units in the square is easy: one, two, three, etc..
But, how can you count all the square units in the ellipse? How do you decide what part of a square is under the top curve? What about the curves at the left and right ends?
Fortunately, mathematics has a fast way to add up all the square units without actually counting them.
Square units are the measurement unit for area because plane figures or flat shapes can always be divided into squares of known dimensions, like these:
- m