When To Use Sin Cos Tan In Physics

Could Someone Please Explain Sin Cos And Tan In A Simple Way

I haven’t taken this in school yet but I love math and physics and join lots of competitions. I have a problem with sine, cosine, and tangent, that I really need a SIMPLE explanation along with an example. I know for a first that they are related to angles and are used in physics, so how are they calculated and how are they used?

Thanks in advance

• $\begingroup$Why a downvote for such a valuable question ? Everyone was once a beginner.$\endgroup$ user65203Nov 3, 2020 at 8:51
• 1Nov 3, 2020 at 8:56
• 1Nov 3, 2020 at 8:57
• 5$\begingroup$@YvesDaoust I wouldn’t downvote it, but I’m tempted to close-vote for being too broad / needs more focus.$\endgroup$Nov 3, 2020 at 8:58
• 3$\begingroup$@PM2Ring: yep, and we have a “happy end”.$\endgroup$ user65203

It is all about triangles and relations between the side lengths and angle amplitudes.

In a right triangle, by definition,

$$\cos=\frac AC$$

$$\sin=\frac BC$$

$$\tan=\frac BA$$

Using these three interrelated functions, you can solve a real lot of geometric problems, such as relations between angles and sides of a general triangle, or even a triangle drawn on a sphere, and do topography, mechanics, geography, GPS, optics, astronomy… and more.

It turns out that these functions also have a deep meaning in maths and they are about as essential as the four basic operations and exponentiation. But this is an advanced topic.

$$\cos\approx1-\frac2+\frac-\frac+\cdots$$

and the more terms you add, the closer you get to the exact value.

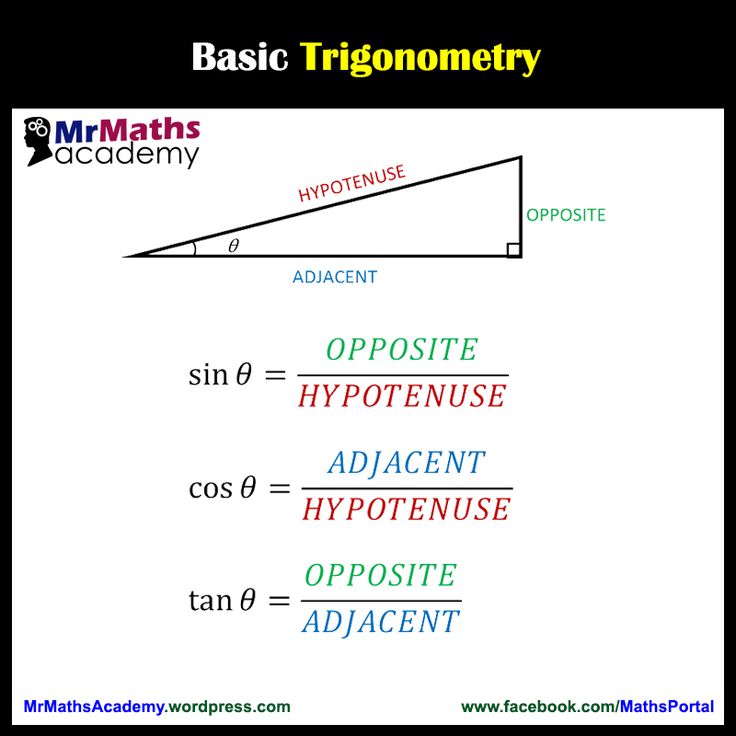
Examples Using Sin Cos Tan Formulas

Example 1: Using the triangle below, find the value of sin A, cos A, and tan A. using sin cos tan formulas.

Using sin cos tan formulas,

Sin A = Side opposite to angle A / Hypotenuse

= BC/AB

Cos A = Side adjacent to angle A / Hypotenuse

= AC/AB

tan A = Opposite side/Adjacent side

= BC/AC

Answer: sin A = 5/13, cos A = 12/13, and tan A = 5/12.

Example 2: If sin A = 6/10 and cos A = 8/10, calculate tan A.

Solution:

Using sin cos tan formulas,

tan A = sin A / cos A

= 3/4

Answer: tan A = 3/4.

Example 3: If csc A = 5/3 and sec A = 5/4, find the value of tan A.

Solution:

Using sin cos tan formulas,

sin A = 1/csc A = 1 / = 3/5

cos A = 1/sec A = 1 / = 4/5

tan A = sin A / cos A

Sine Cosine And Tangent

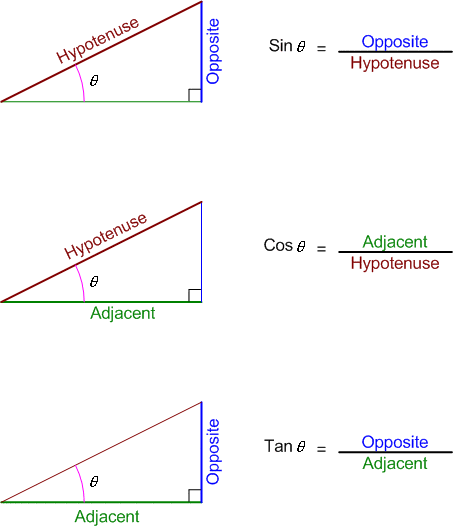
And Sine, Cosine and Tangent are the three main functions in trigonometry.

They are often shortened to sin, cos and tan.

The calculation is simply one side of a right angled triangle divided by another side … we just have to know which sides, and that is where “sohcahtoa” helps.For a triangle with an angle , the functions are calculated this way:

Read Also: What Does M Stand For In Physics

Vector Components And Trigonometry

So what do you do when you have triangles that are not 30-60-90, 45-45-90 or 3-4-5. And where did that 37-53-90 angle for the 3-4-5 triangle come from anyways?

You may have heard mention of the sine wave or sine function which looks like the above wave. The wavelike nature of the sine function will be treated later this year. For now, we will examine the relationship of the sine function to simple right angle triangles.

If we take a right triangle with an angle , we can label the sides of the triangle. The side of the triangle next to the angle we call the adjacent side of the triangle. The side of the triangle opposite the angle we call the opposite side of the triangle. And the long side of the triangle we call the hypotenuse .

Using these labels, we have a mnemonic that can be used to remember the relationship between the length of the sides of a triangle and the angles in that triangle.

SohCahToa

S is for Sine

C is for Cosine

T is for Tangent

o is for opposite

a is for adjacent

h is for hypotenuse

So the Sine of the angle is equal to the length of the opposite side divided by the length of the hypotenuse

To actually calculate the sine of an angle by hand is tricky, and we will address this later. In the old days, one had to memorize a trigonometry table. Now, you can hit a button on your calculator. So when you enter Sin 20° on your calculator, it approximately gives you 0.34 .

Now let us examine a 20° triangle where the hypotenuse has a length of 1.

Trigonometry In Video Games:

Have you ever played the game, Mario? When you see him so smoothly glide over the road blocks. He doesnt really jump straight along the Y axis, it is a slightly curved path or a parabolic path that he takes to tackle the obstacles on his way. Trigonometry helps Mario jump over these obstacles. As you know Gaming industry is all about IT and computers and hence Trigonometry is of equal importance for these engineers.

In construction we need trigonometry to calculate the following:

• Measuring fields, lots and areas
• Making walls parallel and perpendicular
• Installing ceramic tiles
• Roof inclination
• The height of the building, the width length etc. and the many other such things where it becomes necessary to use trigonometry.

Architects use trigonometry to calculate structural load, roof slopes, ground surfaces and many other aspects, including sun shading and light angles.

Recommended Reading: How To Say Biology In Spanish

The One About Trigonometry

Last Updated on June 23, 2022 by Laura Turner

Im guessing that by this point in your MCAT preparation you feel like youve parked a dump truck full of information next to your desk and shoveled facts into your brain until its about ready to burst. And then you hit that physics problem. The one that requires you to know the sine or is that cosine? of 60 degrees.

You search through your mental hard drive for references to trigonometry. Theres something about SOH CAH TOA and a2 and b2. Oh dear. Something else to add to the to memorize list thats growing to the thickness of your organic chemistry textbook.

There are lots of videos and articles about tricks for memorizing sine and cosine values, and they are a good starting point, but they arent actually that helpful for the MCAT. . All you really need to memorize to do any trigonometry calculation on test day is syne point 5, point 7, point 9. Thats it! Lets see how this works

In the picture below, we see two right triangles inscribed over a unit circle: one with its hypotenuse at an angle of 30° with the x-axis and one with its hypotenuse at an angle of 60° with the x-axis. Because sine = opposite/hypotenuse , the sine of an angle relates the length of the side of the triangle in the y-direction with the hypotenuse. To remember this, it can be helpful to think of sine and y having similar sounds. Thats why we write sine as syne in the rhyme.

a) 1.63kgc) 4.00kgd) 6.21kg

Trigonometry In Flight Engineering:

Flight engineers have to take in account their speed, distance, and direction along with the speed and direction of the wind. The wind plays an important role in how and when a plane will arrive where ever needed this is solved using vectors to create a triangle using trigonometry to solve. For example, if a plane is travelling at 234 mph, 45 degrees N of E, and there is a wind blowing due south at 20 mph. Trigonometry will help to solve for that third side of your triangle which will lead the plane in the right direction, the plane will actually travel with the force of wind added on to its course.

You May Like: How Do You Do Percent Error In Chemistry

How To Find Sin Cos Tan Values

To remember the trigonometric values given in the above table, follow the below steps:

• First divide the numbers 0,1,2,3, and 4 by 4 and then take the positive roots of all those numbers.
• Hence, we get the values for sine ratios,i.e., 0, ½, 1/2, 3/2, and 1 for angles 0°, 30°, 45°, 60° and 90°
• Now, write the values of sine degrees in reverse order to get the values of cosine for the same angles.
• As we know, tan is the ratio of sin and cos, such as tan = sin /cos . Thus, we can get the values of tan ratio for the specific angles.

Sin Values

Trig Calculator Finding Sin Cos Tan Cot Sec Csc

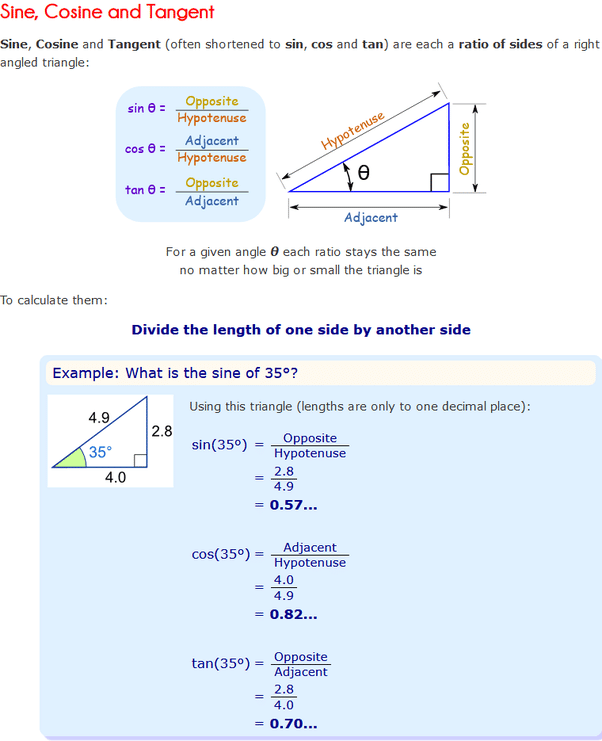
To find the trigonometric functions of an angle, enter the chosen angle in degrees or radians. Underneath the calculator, the six most popular trig functions will appear – three basic ones: sine, cosine, and tangent, and their reciprocals: cosecant, secant, and cotangent. Additionally, if the angle is acute, the right triangle will be displayed, which can help you understand how the functions may be interpreted.

Recommended Reading: What Are Cations And Anions In Chemistry

What Is All Sin Tan Cos Rule

Trigonometry is an important branch of mathematics, it deals with the relationship of sides with angles in a right-angle triangle. Trigonometry is important in physics also, it is used to find, the height of towers, the distance between stars, or in the Navigation systems. Trigonometry is predicated on the principle that If two triangles have an equivalent set of angles then their sides are within the same ratio. Side lengths are often different but side ratios are equivalent.

Can Trigonometry Be Used In Everyday Life

Trigonometry may not have its direct applications in solving practical issues, but it is used in various things that we enjoy so much. For example music, as you know sound travels in waves and this pattern though not as regular as a sine or cosine function, is still useful in developing computer music. A computer cannot obviously listen to and comprehend music as we do, so computers represent it mathematically by its constituent sound waves. And this means sound engineers need to know at least the basics of trigonometry. And the good music that these sound engineers produce is used to calm us from our hectic, stress full life All thanks to trigonometry.

Read Also: What Is Movement In Geography

What Are Sine Cosine And Tangent

What do sines, cosines, and tangents have to do with right triangles? And what are the “sin,””cos,” and “tan” buttons on your calculator for? Keep reading to find out!

• The ratios of the sides of a right triangle are completely determined by its angles.
• Because there are three sides of a triangle means that there are also three possible ratios of the lengths of a triangle’s sides.
• These three ratios are the sine, cosine, and tangent trigonometric functions.

Do you know what two angles living inside the same right triangle said to each other? The first angle goes, Hey Thelma , I dont mean to go off on a tangent here, but whats your sine? To which the second angle replies, Phil , I dont know why you even bother to ask, my sine is obviously the same as your cosine!

Okay, so maybe thats not the best joke in the world, but once you understand sines and cosines, it is kind of funny. Of course, that means that if you dont know the difference between a sine and a cosine, youre currently left out in the metaphorical cold.

Clearly we cant let that happenand we wont! Because today were going to learn all about sines, cosines, and tangents.

Trigonometry Can Be Used To Measure The Height Of A Building Or Mountains:

if you know the distance from where you observe the building and the angle of elevation you can easily find the height of the building. Similarly, if you have the value of one side and the angle of depression from the top of the building you can find and another side in the triangle, all you need to know is one side and angle of the triangle.

Don’t Miss: What Is Experimental Research In Psychology

Trigonometry Used In Navigation:

Trigonometry is used to set directions such as the north south east west, it tells you what direction to take with the compass to get on a straight direction. It is used in navigation in order to pinpoint a location. It is also used to find the distance of the shore from a point in the sea. It is also used to see the horizon.

Its March, which means March Madness for fans of college basketball. Mathnasium recently joined CBS to discuss March Mathness – the statistics that go into building the perfect bracket for the tournament! You can check out the segment..

Math Enrichment and Accelerated Programs in Pflugerville

Did you know Mathnasium offers enrichment programs for students? Mathnasium is where students in grades K-12 come to catch up, keep up, and get ahead in math! Students and their parents seeking to stay ahead and excel to their fullest potent..

Application Of Sin Cos Tan In Real Life

Trigonometry ratios sin, cos, tan find application in finding heights and distances in our daily lives. We use sin, cos, and tan to solve many real-life problems. Here is an example to understand the applications of sin, cos and tan.

Example: A ladder leans against a brick wall making an angle of 50o with the horizontal. If the ladder is at a distance of 10 ft from the wall, then up to what height of the wall the ladder reaches?

Solution:

Let us assume that the ladder reaches till x ft of the wall.

Using the given information:

Here, we know the adjacent side and we have to find the opposite side . So we use the relation between the opposite and the adjacent sides which is tan.

tan 50o = x/10

x = 10 tan 50o

x 11.9 ft

Here, tan 50o is calculated using the calculator and the final answer is rounded up to 1 decimal. Therefore, the ladder reaches up to 11.9 ft of the wall.

Topics Related to Sin Cos Tan:

Read Also: Why Is Chemistry Important In The Study Of Biology

Sin Cos Tan On Unit Circle

The values of sin, cos, and tan can be calculated for any given angle using the unit circle. Unit circle in a coordinate plane is a circle of unit radius of 1, frequently centered at the origin in the Cartesian coordinate system in the Euclidean plane, especially in trigonometry. For any point on unit circle, given with the coordinates, the sin, cos and tan ratios can be given as,

where is the angle the line joining the point and origin forms with the positive x-axis.

What Is Sin Cos Tan In Trigonometry

Sin, cos, and tan are the three primary trigonometric ratios, namely, sine, cosine, and tangent respectively, where each of which gives the ratio of two sides of a right-angled triangle. We know that the longest side of a right-angled triangle is known as the “hypotenuse” and the other two sides are known as the “legs.” That means, in trigonometry, the longest side of a right-angled triangle is still known as the “hypotenuse” but the other two legs are named to be:

• opposite side and

We decide the “opposite” and “adjacent” sides based upon the angle which we are talking about.

• The “opposite side” or the perpendicular is the side that is just “opposite” to the angle.
• The “adjacent side” or the base is the side that “touches” the angle.

Also Check: What Is Activation Energy Biology

What Are Sin Cos Tan Formulas

The sincostan formulas are defined for a right triangle. Let us consider a right triangle ABC that is right angled at C. Then AB is the longest side and hence it is called the hypotenuse. AC and BC are the sides that are adjacent and opposite to the angle A respectively. The trigonometric ratios sin, cos, and tan for the angle A are as follows.

Trigonometry Calculator As A Tool For Solving Right Triangle

To find the missing sides or angles of the right triangle, all you need to do is enter the known variables into the trigonometry calculator. You need only two given values in the case of:

• one side and one angle
• area and one side

Remember that if you know two angles, it’s not enough to find the sides of the triangle. Two triangles having the same shape may be of different sizes – that kind of relationship is called triangle similarity. If the sides have the same length, then the triangles are congruent.

Recommended Reading: Electron Pair Geometry Of H2o

The Attempt At A Solution

2,106

216

7

2

0

Smith96 said:I am still confused how to know which one to use. I drew the FBD for both problems and now I am staring at the charts trying to figure out why sin was used and why cos was used, in order to know which to use next time..

216

7

For the first, )=40NFor the second, =120J

W = Fd

Intro To The Trigonometric Ratios

• When i should use Cos ? Sin ? Tan?AnswerAnswer Leory Ma’s post When i should use Cos ? S…Button opens signup modalComment on Leory Ma’s post When i should use Cos ? S…
• Posted 12 years ago. Direct link to Christine Sankar’s post To help you to better und…moreTo help you to better understand when to use the forms Sin-Cos-Tan you can use SOH CAH TOA….SOH:Sin is used when given the opposite and the hypotenuse CAH:Cos is used when given the adjacent and the hypotenuse TOA:Tan is used when given the opposite and adjacent for eg. If you are given a triangle where the two significantly shorter sides are given and you wish to obtain the longest side termed the hypotenuse, you recognize that it satisfies the terms necessary to use the either the SOH or CAH form You therefore proceed to identify which is the adjacent and which is the opposite. The opposite, which is clearly identifiable due to its name, is the side which is directly OPPOSITE the given angle.The adjacent is therefore the side which forms a 90° angle to the opposite.For eg. purposes, the given angle is 45°. So you then proceed to imply due to the SOH form that Sin45= opposite divided by the hypotenuse. In order for you to obtain the hypotenuse we transpose for the hypotenuse to become the subject of the formula. By cross multiplying we obtain the formula:Hypotenuse = Opposite divided by Sin45. Hope this helps.

Also Check: What Is V In Physics