Recognizing Direct Or Indirect Variation
You might be asked to look at functions s to unique \s well discuss later in theAlgebraic Functions section) and determine if they are direct, inverse, or neither:
| Function | Direct, Inverse, or Neither Variation |
| \ | Neither: Direct Variation line must go through \\). . |
| \ | Direct: This is the same as \. |
| \ | |
| 8 | 16 |
Inverse8InverseNeither
| \ | |
| 6 | 8 |
Neither
What Is Made Possible To Learn When Using The Variation Theory Of Learning In Teaching Mathematics
The variation theory of learning emphasizes variation as a necessary condition for learners to be able to discern new aspects of an object of learning. In a substantial number of studies, the theory has been used to analyze teaching and students learning in classrooms. In mathematics education, variation theory has also been used to explore variation in sets of instructional examples. For example, it has been reported how teachers, by using variation and invariance within and between examples, can help learners to engage with mathematical structure.
- Math examples and question always vary – we assume that practice with varied examples bring fluency.
- It may bring fluency, but in a machine like way.
- Controlling variation in examples and question can bring understanding.
- We notice what varies when other things are held stable.
- We notice what is constant when everything else varies.
- If everything varies we don’t know what to focus on.
” Mathematics is about relationships when see the effects of one thing varying we can generalize about a relationship when we generalize about a relationship we are learning a concept. ”
Date:13th of April’ 2021
Director of Matho Logics
Modern Definition And Relation To Measure Theory
Classically right-continuous functions of bounded variations can be mapped one-to-one to signed measures. More precisely, consider a signed measure $\mu$ on $\mathbb R$ with finite total variation . We then define the function\begin\labelF_\mu := \mu \, .\end
Theorem 2
- For every signed measure $\mu$ with finite total variation, $F_\mu$ is a right-continuous function of bounded variation such that $\lim_ F_\mu = 0$ and $TV $ equals the total variation of $\mu$ )$.
- For every right-continuous function $f:\mathbb R\to \mathbb R$ of bounded variation with $\lim_ f = 0$ there is a unique signed measure $\mu$ such that $f=F_\mu$.
Moreover, the total variation of $f$ equals the total variation of the measure $\mu$ .
For a proof see Section 4 of Chapter 4 in . Obvious generalizations hold in the case of different domains of definition.
Recommended Reading: What Is Bachelor Of Psychology
Help Others Learning Math Just Like You
âââââ
We hope you found this Math math tutorial “Variation. Types of Variation” useful. If you did it would be great if you could spare the time to rate this math tutorial and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of math and other disciplines.
Variation Types Of Variation

| Tutorial ID |
|---|
In this Math tutorial, you will learn:
- What is variation?
- What are the three types of variation?
- Where does variation differ from proportion?
- Where to use proportional and variation approach in graph problems?
- What is the constant of proportionality used in variation?
- What is the shape of the graph that illustrates direct/inverse variation?
- Which are the properties of variation?
You May Like: What Is Earth Movement In Geography
Module : Rational And Radical Functions
- Solve inverse variation problems.
- Solve problems involving joint variation.
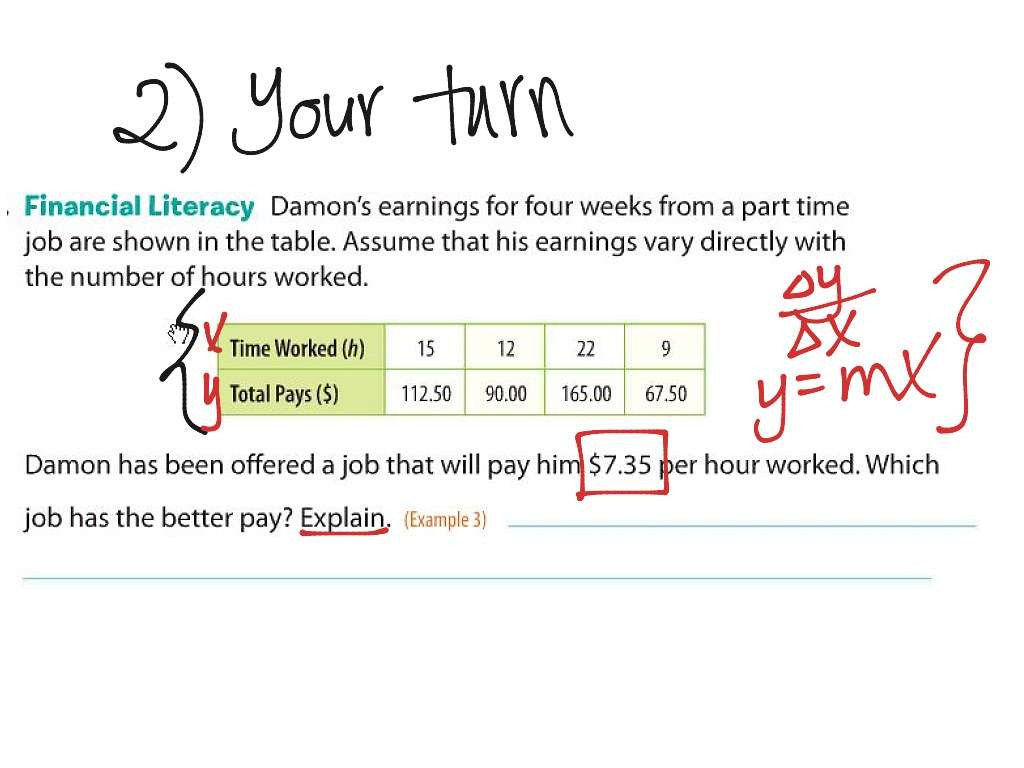
A used-car company has just offered their best candidate, Nicole, a position in sales. The position offers 16% commission on her sales. Her earnings depend on the amount of her sales. For instance if she sells a vehicle for $4,600, she will earn $736. She wants to evaluate the offer, but she is not sure how. In this section we will look at relationships, such as this one, between earnings, sales, and commission rate.
How To Solve Direct Variation
To solve direct variation, plug in matching values of variables to find k. Then, if necessary, use the value of k with a value of x or y to find the other variables value.
Example 1: Solving A Direct Variation For k
Lets say that there is a direct variation between x and y. That means:
- y = kx
for some constant k.
Lets assume we know that y = 15 when x = 3. Plugging in these values of x and y, we get:
- y = kx
So, y = 42 when x = 7.
Also Check: What Is Gradualism In Biology
A General Note: Direct Variation
If x and y are related by an equation of the form
y=k^
then we say that the relationship is direct variation and y varies directly with the nth power of x. In direct variation relationships, there is a nonzero constant ratio k=\dfrac^}, where k is called the constant of variation, which help defines the relationship between the variables.
How To Tell If A Graph Is A Direct Variation
To tell if a graph is a direct variation, look for a line that passes through the origin. In particular, this means:
- The graph is a line .
- The slope is constant .
- The line goes through the origin ).
Example 1: A Graph That Is A Direct Variation
Consider the graph:
This graph is a direct variation, since:
- The graph is a line .
- The slope is constant .
- The line goes through the origin ).
Example 2: A Graph That Is Not A Direct Variation
Consider the graph:
This graph is not a direct variation, since:
- The graph is not a line .
Example 3: A Graph That Is Not A Direct Variation
Consider the graph:
This graph is not a direct variation, since:
- The line does not pass through the origin .
Read Also: Select Operation In Relational Algebra In Dbms
Example: Solving A Direct Variation Problem
The quantity y varies directly with the cube of x. If y=25 when x=2, find y when x is 6.
The general formula for direct variation with a cube is y=k^. The constant can be found by dividing y by the cube of x.
\begin k& =\dfrac^} \\ & =\dfrac^}\\ & =\dfrac\end
Now use the constant to write an equation that represents this relationship.
y=\dfrac^
Substitute x=6 and solve for y.
\beginy& =\dfrac^ \\ & =675\hfill \end
Analysis of the Solution
What Is Direct Variation Formula
Direct variation formula helps relate two quantities, having a mathematical relationship such that one of the variables is a constant multiple of the other. When two quantities are directly proportional to each other or are in direct variation they are represented using the symbol “\”. Suppose there are two quantities x and y that are in direct variation then they are expressed as follows:
y \ x
When the proportionality sign is removed then the direct variation formula is given as follows.
Read Also: What Is Displacement In Chemistry
How To: Given A Description Of A Direct Variation Problem Solve For An Unknown
Math Review Of Direct Inverse Joint And Combined Variation

Overview:
Equations that describe the relationship between two variables in a sentence express the variation between those variables. Examples of types of variation include direct, inverse, joint, and combined variation.
What Is Direct Variation?
In direct variation, as one variable is multiplied by a constant and increases, another variable also increases. Suppose Jane works at McDonalds and is paid $9.35 per hour. Her total wages vary directly with the amount of hours she works. If she works 1 hour, her gross wages are $9.35, and if she works 2 hours her gross wages are $18.70. If she works 8 hours, her wages are $74.80. If the hours she works are plotted on the x axis against her wages on the y axis, the resulting line is a straight line showing direct variation.
What Is Inverse Variation?
Inverse variation is a relationship between variables so that as one variable decreases the other variable increases. The equations expressing inverse variation take the form xy = k, where k is a constant, as well as y = k/x.. For example, the current c varies inversely with the resistance in ohms r. When the current is 40 amps, the resistance is 12 ohms. When the current is 24 amps, the resistance is 20 ohms. If the current is plotted on the x axis, and the resistance is plotted on the y axis, the graph is in 2 separate curves called a hyperbola.
What Is Joint Variation?
What Is Combined Variation?
Don’t Miss: What Is Association In Chemistry
What Do These Variation
The keywords’ meanings are:
- directly: things are working together you are multiplying everything.
- inversely: things working against each other you are dividing something somewhere.
- jointly: many things are working together you are multiplying lots of stuff.
An example of a variation equation would be the formula for the area of the circle:
A = r2
In the language of variation, this equation means:
the area A varies directly with the square of the radius r
…and the constant of variation is k = . This formula is an example of “direct” variation.”Direct variation” means that, in the one term of the formula, the variable is “on top”.
Affiliate
On the other hand, “inverse variation” means that the variable is underneath, in the bottom of a fraction. Suppose, for instance, that you inherit a money market account containing $100,000, and you wonder how much money your rich uncle initially invested eight years ago. Depending on the average interest rate “r“, the formula you would use would be:
…where P is the principal that your uncle invested. In the language of variation, this formula reads as:
the principal P varies inversely with
…with the constant of variation being k = 100,000.
The other case of variation is “jointly”. “Joint variation” means “directly, but with two or more variables”. An example would be the formula for the area of a triangle with base “b” and height “h“:
In words:
the area A varies jointly with b and h
- “F varies as x” means F = kx
Origins Of Variation Theory
The study of Variation Theory arises mainly from work across two groups of researchers who arrived at similar, but not exactly the same conclusions.
One was Swedish researcher Ference Marton and colleagues who worked on the concept of Variation Theory the other was Gu Ling Yuan and his team in Shanghai who called it Bianchi . As one would expect, the emergence of two similar theories has caused confusion in some areas of the sector. In the context of the United Kingdom, the distinction between them is rarely made and so aspects of Bianchi are used under Variation Theory.
They both agree that the central idea of teaching with variation is to highlight the essential features of the concepts through varying the non-essential features. . This blog will mainly draw on the learning study of Gu and his team.
The application of Variation Theory is much wider than just the domain of mathematics teaching, but rather as a theory that underpins how students learn anything. The principle that underpins the theory is that new learning occurs when they understand how a critical aspect of a new concept changes against something that does not change .
It is unlikely that a worksheet on its own will bring about the required cognitive process in students needed to benefit from the advantages that Variation Theory offers students in their conceptualisation of mathematical structures.
You May Like: Kuta Software Infinite Geometry Secant Angles Answers
What Is Variation Theory A Guide For Primary Maths Teachers
Neil Almond
This blog will look at the concept of Variation Theory and attempt to demystify the confusing language surrounding it. It is hoped that this will make Variation Theory an accessible and exciting tool that you can begin to use in your maths lessons, or give you an understanding of what is happening if you recognise the principles, despite never having heard of Variation Theory before!
If you are a premium member of Third Space Learning, you can access a whole-school CPD presentation that covers these points in our Maths Hub.
What Is Variation Theory In Primary Maths
Variation Theory is a general theory of learning that is used predominantly in mathematics teaching and pedagogy. It emphasises a concepts essential features by focusing on what is kept the same and what changes, which offers the opportunity to make meaningful connections.
FREE Crib Sheet for Primary School Staff Meetings
Read Also: What Does K Stand For In Math
Example: Solving An Inverse Variation Problem
A quantity y varies inversely with the cube of x. If y=25 when x=2, find y when x is 6.
The general formula for inverse variation with a cube is y=\dfrac^}. The constant can be found by multiplying y by the cube of x.
\begink& =^y \\ & =^\cdot 25 \\ & =200 \end
Now we use the constant to write an equation that represents this relationship.
\beginy& =\dfrac^},\hspacek=200 \\ y& =\dfrac^} \end
Substitute x=6 and solve for y.
\beginy& =\dfrac^} \\ & =\dfrac \end
Analysis of the Solution
\dfrac
The following video presents a short lesson on inverse variation and includes more worked examples.
*footnote: Why Square The Differences
If we just add up the differences from the mean … the negatives cancel the positives:
| 4 + 4 4 44 = 0 |
So that won’t work. How about we use absolute values?
| |4| + |4| + |4| + |4|4 = 4 + 4 + 4 + 44 = 4 |
That looks good , but what about this case:
| |7| + |1| + |6| + |2|4 = 7 + 1 + 6 + 24 = 4 |
Oh No! It also gives a value of 4,Even though the differences are more spread out.
So let us try squaring each difference :
| 2 + 24) = = 4 | |
| 2 + 24) = = 4.74… |
That is nice! The Standard Deviation is bigger when the differences are more spread out … just what we want.
In fact this method is a similar idea to distance between points, just applied in a different way.
And it is easier to use algebra on squares and square roots than absolute values, which makes the standard deviation easy to use in other areas of mathematics.
You May Like: What Does Ageing Population Mean In Geography
Differences In What Was Made Possible To Discern
There were general similarities between Lesson 1 and Lesson 2 . For instance, the lessons were about the same length and the same method for solving equations with one unknown was taught. In both lessons, the students worked with creating equations with one unknown for a fellow student. We focused on similarities and differences in enacted example spaces in order to explore, on a micro-level, effects of the intervention on teaching practice. We analyzed the examples introduced by the teacher during whole-class discussion using a variation-theory framework . Our analysis shows that the enacted object of learning, and thereby what was made possible to learn in the lesson, had changed. In L1, the object of learning entailed primarily the method and procedure for solving, by finding answers to equations with one unknown. When the same teacher taught L2 on the same topic after the intervention, the answers to the equations used in the lesson were already known, and the object of learning was instead about understanding the structure of an equation: how an equation can be created and the operations used in solving it.
What Is Direct Variation
Direct variation exists between any two variables when one quantity is directly dependent on the other i.e. if one quantity increases with respect to the other quantity and vice versa. It is the relationship between two variables where one of the variables is a constant multiple of the other. Since the two variables are directly related to each other it is also termed as directly proportional.
Direct variation and inverse variation are two types of proportionalities. Proportionality refers to a relationship where two quantities are multiplicatively connected by a constant. In a direct variation, the ratio of the two quantities remains the same whereas in an inverse variation the product of the two quantities remains constant. Here we shall check in detail the definition and examples of direct variation.
Read Also: What Is An Example Of Framing In Psychology
Can Direct Variation Be Negative
Direct variation can be negative. To be more precise, the constant of variation k can be less than zero .
In practical terms, k < 0 means that y decreases as x increases. Similarly, y increases as x decreases.
For example, if k = -5, then we have the direct variation y = -5x.
When x increases by 1, y will decrease by 5.
When x decreases by 1, y will increase by 5.
The graph will be a line that goes through the origin and moves down as we move from left to right. The slope is -5 = -5 / 1 = rise / run, so we move down 5 units for every unit we move right.
Wiener’s And Young’s Generalizations
One sometimes also considers classes $BV_\Phi $ defined as follows. Let $\Phi: \to \mathbb R$, we let $TV_ $ be the least upper bound of sums of the type\where $a\leq x_1 < \ldots < x_< b$ is an arbitrary family of points. The quantity $TV_\Phi $ is called the $\Phi$-variation of $f$ on $$. If $TV_\Phi < \infty$ one says that $f$ has bounded $\Phi$-variation on $$, while the class of such functions is denoted by $BV_\Phi $ . If $\Phi =u$, one obtains Jordan’s class $BV $, while if $\Phi =u^p$, one obtains Wiener’s classes $BV_p $ . The definition of the class $BV_\Phi $ was proposed by L.C. Young in .
If\then\)\subset BV_ \subset BV_q \subset BV_)} \subset BV_)} \, .\]for $1\leq p < q$ and $0< \alpha< \beta< \infty$, these being proper inclusions.
Also Check: What Is Binding Energy In Nuclear Physics