Circle Geometry Rules Grade 9

Circle Theorems: Where Do They Come From

In my opinion, the most important shape in maths is the circle. Its so simple to understand, but it also gives us one of the most crucial constants in all of mathematics, p. Once we draw some lines inside a circle, we can deduce patterns and theorems that are useful both theoretically and in a practical sense. The defining feature of the circle is its constant radius, and I hope to show you that starting from this simple line, we can derive all the circle theorems you need to understand. Ready? Lets go.

Firstly, we have to know how to construct an isosceles triangle from two radii. Well be doing this a lot, so heres an example:

Since every radius is the same, drawing two radii forms a triangle with two equal sides an isosceles triangle!

Now for the theorems:

Theorem: Opposite Angles Of A Cyclic Quadrilateral

The opposite angles of a cyclic quadrilateral are supplementary.

s cyclic quad.)

Circle with centre \ with points \ and \ on the circumference such that \ is a cyclic quadrilateral.

\ and \

Draw \ and \. Label \ and \. \ Similarly, we can show that \.

Converse: interior opposite angles of a quadrilateral

If the interior opposite angles of a quadrilateral are supplementary, then the quadrilateral is cyclic.

Exterior angle of a cyclic quadrilateral

If a quadrilateral is cyclic, then the exterior angle is equal to the interior opposite angle.

Perpendicular Line From Center Bisects Chord

In the circle with centre \, \, \ units and \. Determine \.

In the circle with centre \ and radius \ units, \ and \. Determine \.

In the circle with centre \, \, \ units and \ units. Determine \.

In the circle with centre \, \, \, \ units, \ units and \ units. Determine \.

In the circle with centre \, \, \, \ units, \ units and \ units. Determine \.

Also Check: Geometry Dash Hack No Jailbreak

What Is The Chord Of A Circle

A line segment, which joins any two points on the circles circumference, is known as a chord of the circle. Diameter is the largest chord which passes through the centre of the circle.

Let us consider a circle, which has AB as diameter, CD is the chord of the circle and OE is the radius. See the figure below.

Let us see the different circle theorems.

Circles Theorem Class 9

In Class 9, students will come across the basics of circles. Here, we will learn different theorems based on the circles chord. The theorems will be based on these topics:

• Angle Subtended by a Chord at a Point
• The perpendicular from the Centre to a Chord
• Equal Chords and their Distances from the Centre
• Angle Subtended by an Arc of a Circle
• Cyclic Quadrilaterals

Now let us learn all the circle theorems and proofs.

Don’t Miss: Algebra 1 Age Word Problems

Going From One Term To The Next

A list of numbers which form a pattern is called a sequence. Each number in a sequence is called a term of the sequence. The first number is the first term of the sequence.

Write down the next three numbers in each of the sequences below. Also explain in writing, in each case, how you figured out what the numbers should be.

Numbers that follow one another are said to be consecutive.

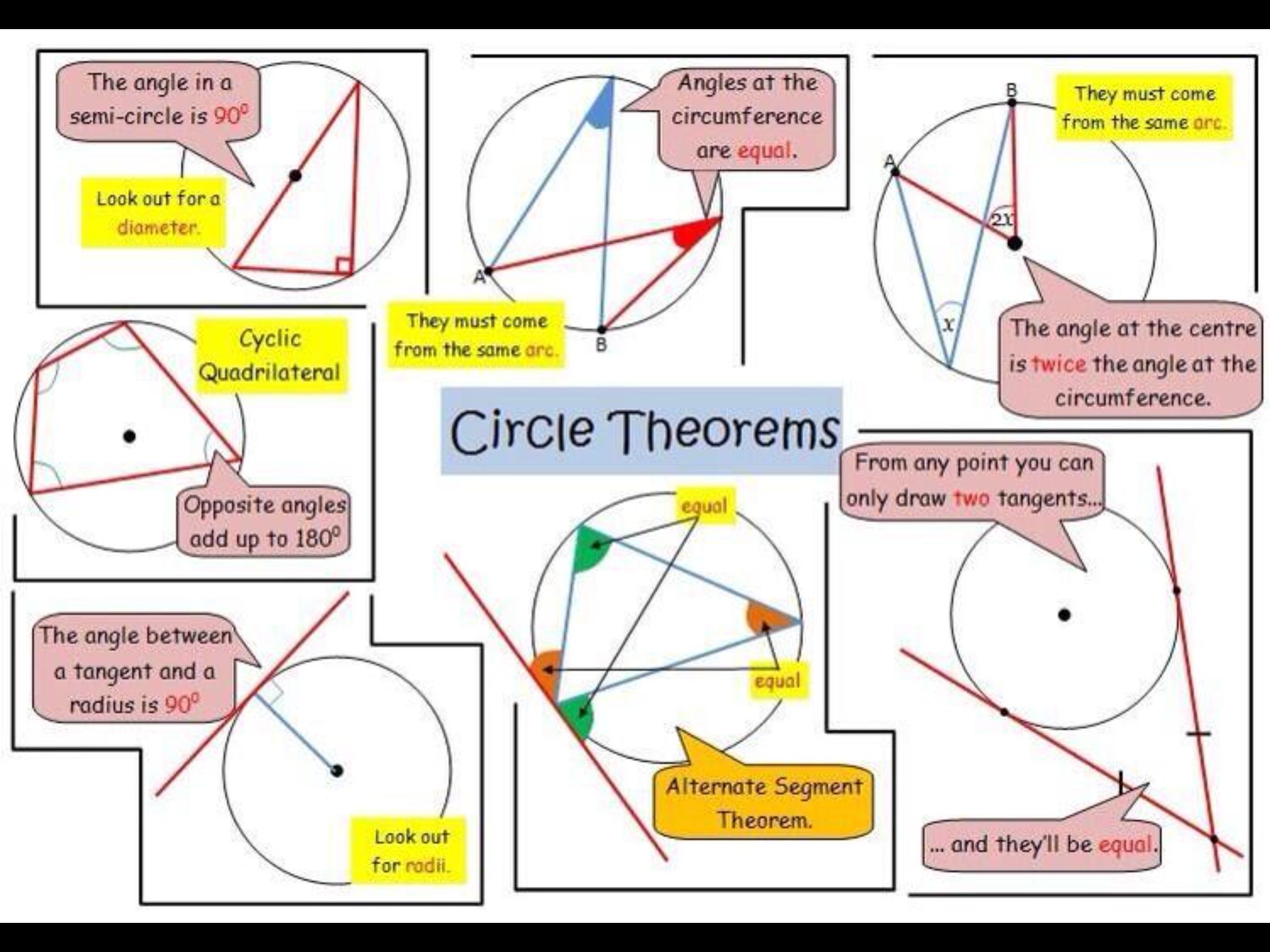
The Angle In A Semicircle Is A Right Angle:

Firstly, we can see that this is an application of the theorem above, with angle at the centre = 180°. If we wanted to show this without using Theorem 1, start by drawing a line from A to C. Note that this is a radius of the circle. This makes three triangles: ABC, ACD and a large one, BCD. We also have that ABC and ACD are isosceles.

Firstly, we see that a+b=180° .

For ABC, we can see that b+2s=180° .

And for ACD we have that a+2t=180° .

If we add equations and , we have b+2s+a+2t = 360°. We also know that a+b=180°. So:

2s+2t+180° = 360°

s+t = 90°, which is what we were after.

Don’t Miss: Hawkes Learning System Software

Neither Adding Nor Multiplying By The Same Number

There are sequences where there is neither a constant difference nor a constant ratio between consecutive terms and yet a pattern still exists, as in the case of sequences B and E.

Adding Or Subtracting The Same Number

Recommended Reading: Holt Geometry Lesson 4.5 Practice B Answers

Rules Of Circle Geometry

Opposite Angles In A Cyclic Quadrilateral Sum To 1:

Angle at B + angle at D = angle at C + angle at E = 180°

A cyclic quadrilateral is a quadrilateral where all the corners are on the circumference of a circle.

As before, the first step is to draw radii from the centre to each corner of the quadrilateral. This gives us four isosceles triangles: ABC, ACD, ADE and ABE.

We know that the sum of the interior angles of a quadrilateral is 360° . With this, we see:

Angle B Angle C Angle D Angle E

+ + + = 360°

2u + 2v + 2w + 2x = 360°

u + v + w + x = 180°

So we have:

+ = 180°

Angle C + Angle E

+ = 180°

Also Check: Is Paris Jackson Biological Daughter

Theorem: Subtended Angles In The Same Segment Of A Circle Are Equal

If the angles subtended by a chord of the circle are on the same side of the chord, then the angles are equal.

s in same seg.)

Circle with centre \, and points \ and \ on the circumference of the circle. Arc \ subtends \ and \ in the same segment of the circle.

Equal arcs subtend equal angles

From the theorem above we can deduce that if angles at the circumference of a circle are subtended by arcs of equal length, then the angles are equal. In the figure below, notice that if we were to move the two chords with equal length closer to each other, until they overlap, we would have the same situation as with the theorem above. This shows that the angles subtended by arcs of equal length are also equal.

Multiplying Or Dividing With The Same Number

Take another look at sequence F: 2 6 18 54 162 486 …

Piet explains that he figured out how to continue the sequence F:

I looked at the first two terms in the sequence and wrote \.

When I multiplied the first number by 3, I got the second number: \.

I then checked to see if I could find the next number if I multiplied 6 by 3: \.

I continued checking in this way: \ and so on.

This gave me a rule I can use to extend the sequenceand my rule was:multiply each number by 3 to calculate the next number in the sequence.

Zinhle says you can also find the pattern by working backwards and dividing by 3 each time:

The number that we multiply with to get the next term in the sequence is called a ratio. If the number we multiply with remains the same throughout the sequence, we say it is a constant ratio.

You May Like: What Is The Molecular Geometry Of Ccl4

Perpendicular Line From Circle Centre Bisects Chord

If a line is drawn from the centre of a circle perpendicular to a chord, then it bisects the chord.

from centre bisects chord)

Circle with centre \ and line \ perpendicular to chord \.

Draw \ and \.

In \ and in \, \ and \ Therefore \ bisects \.

Alternative proof:

In \ and in \, \ Therefore \ bisects \.

Theorem: Perpendicular Bisector Of Chord Passes Through Circle Centre

If the perpendicular bisector of a chord is drawn, then the line will pass through the centre of the circle.

bisector through centre)

Circle with mid-point \ on chord \.

Line \ is drawn such that \.

Line \ is drawn such that \.

Draw lines \ and \.

Draw lines \ and \.

In \ and in \, \

Similarly it can be shown that in \ and in \, \.

We conclude that all the points that are equidistant from \ and \ will lie on the line \ extended. Therefore the centre \, which is equidistant to all points on the circumference, must also lie on the line \.

Don’t Miss: Who Are Paris Jackson’s Biological Parents

Practice Questions On Circles For Grade 9

Th e diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre. Solution

The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle Solution

Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius 42 cm and also find < OAC and < OCA. Solution

A chord is 12 cm away from the centre of the circle of radius 15 cm. Find the length of the chord. Solution

In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords? Solution

Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord. Solution

Find the value of x° in the following figures :

Using Position To Make Predictions

Sizwe has been thinking about Amanda and Tamara’s explanations of how they worked out the rule for sequence A and has drawn up a table. He agrees with them but says that there is another rule that will also work. He explains:

My table shows the terms in the sequence and the difference between consecutive terms:

Sizwe reasons that the following rule will also work:

Multiply the position of the number by 3 and add 2 to the answer.

I can write this rule as a number sentence:Position of the number\

I use my number sentence to check: \

Also Check: What Is An Example Of Movement In Geography

The Angle At The Centre Is Twice The Angle At The Circumference:

How do we show this? Start by drawing lines to connect A and D, and B and C. This forms three small triangles and one big one . Since the lines AB, AC and AD are all radii of the circle, this means that the triangles ACD, ABD and ABC are isosceles.

So we can see from ABC that the angle at A is 180-2s .

And we have in the larger triangle DCB that:

++ = 180° .

which gives us:

The Angle Between The Chord And The Tangent Is Equal To The Angle In The Alternate Segment:

Finally, one of the more unexpected theorems we can derive from drawing lines in circles. The proof starts in the same way, by drawing radii from the centre of the circle to each of the points B, C and D.

This once again forms three isosceles triangles: ABC, ABD and ACD.

We want to show that a = u+v.

In the larger triangle BCD, we know that:

+ + = 180°

which leads to:

u + v + w = 90°

We also know that:

a = 90° w

Substituting this into :

Read Also: Who Are Paris Jackson’s Biological Parents

Subtended Angles In The Same Segment

Find the values of the unknown angles.

Given \, determine the value of \.

Is \ a diameter of the circle? Explain your answer.

Given circle with centre \, \ and \. Determine \.

Cyclic quadrilaterals

Cyclic quadrilaterals are quadrilaterals with all four vertices lying on the circumference of a circle .

Theorem: Angle At The Centre Of A Circle Is Twice The Size Of The Angle At The Circumference

If an arc subtends an angle at the centre of a circle and at the circumference, then the angle at the centre is twice the size of the angle at the circumference.

Circle with centre \, arc \ subtending \ at the centre of the circle, and \ at the circumference.

Draw \ extended to \ and let \ and \.

Similarly, we can also show that \.

For the first two diagrams shown above we have that: \ And for the last diagram: \

Don’t Miss: Who Is The Biological Father Of Paris Jackson

Angles Subtended By An Arc At The Centre And The Circumference Of A Circle