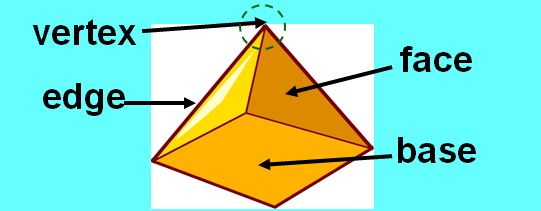
Relation Between Vertices Faces And Edges
The relation between vertices, faces and edges can be easily determined with the help of Eulers Formula. Having learned about the faces, edges, and vertices of solids, let us note an interesting relationship between the three of them. It is to be kept in mind that the formula holds good for closed solids which have flat faces and straight edges such as the cuboids. It cannot be used for cylinders because they have curved edges.
Eulers formula is given by
F + V E = 2
Where F, V, and E are the number of faces, vertices, and edges of the polyhedra respectively.
Vertices Faces And Edges Of Common 3d Shapes
How many faces, edges and vertices does a cuboid have?
A cuboid has 8 vertices.
A cuboid has 12 edges.
A cuboid has 6 faces.
How many faces, edges and vertices does a cylinder have?
A cylinder has 0 vertices.
A cylinder has 2 edges.
A cylinder has 2 faces and 1 curved surface.
How many faces, edges and vertices does a hemisphere have?
A hemisphere has 0 vertices.
A hemisphere has 1 curved edge.
A hemisphere has 1 face and 1 curved surface.
How many faces, edges and vertices does a cone have?
A cone has 1 vertex.
A cone has 1 edge.
A hemisphere has 1 face and 1 curved surface.
How many faces, edges and vertices does a tetrahedron have?
A tetrahedron has 4 vertices.
A tetrahedron has 6 edges.
A tetrahedron has 4 faces.
How many faces, edges and vertices does a sphere have?
A sphere has 0 vertices.
A tetrahedron has 0 edges.
A tetrahedron has 1 curved surface.
How many faces, edges and vertices does a prism have?
A prism is a solid object, geometric shape or polyhedron where the faces of both ends are the same shape. As such, students will come across many types of prisms throughout their schooling. Common ones include cubes, cuboids, triangular prisms, pentagonal prisms and hexagonal prisms.
| Shape |
|---|
| 12 |
What Gets Stored In A Cookie
This site stores nothing other than an automatically generated session ID in the cookie no other information is captured.
In general, only the information that you provide, or the choices you make while visiting a web site, can be stored in a cookie. For example, the site cannot determine your email name unless you choose to type it. Allowing a website to create a cookie does not give that or any other site access to the rest of your computer, and only the site that created the cookie can read it.
Recommended Reading: Lewis Structure Of Ccl4
Heres A List Of Shapes Along With The Number Of Faces Faces Of 3d Shapes Are Given Below:
|
Shape |
Eulers Formula for Polyhedron:
What is Eulers Formula for Types of Polyhedron?
-
The Euler theorem is known to be one of the most important mathematical theorems named after Leonhard Euler.
-
The theorem states a relation of the number of faces, vertices, and edges of any polyhedron.
-
The Eulers formula can be written as F + V = E + 2, where F is the equal to the number of faces, V is equal to the number of vertices, and E is equal to the number of edges.
-
The Eulers formula states that for many solid shapes the number of faces plus the number of vertices minus the number of vertices is equal to 2.
What Is A Basic Definition Of Edge
The word edge most commonly refers to the sharp or angled side of an object or the place where something stops and something else startsa border or margin. Edge is also used as a verb meaning to move sideways. Edge has many additional senses as both a noun and verb.
When its used to refer to the side or tip of an object, the word edge often implies that its sharp or pointy.
- Real-life example: The sharp edge of a knife is the part that you use to cut things with.
- Used in a sentence:I accidentally gave myself a paper cut on the edge of the envelope.
When it refers to the line or border where something stops, edge can be used in the context of objects or places. An edge may be an intentional boundary or it may simply be the place where something ends. Sometimes, it refers to the farthest possible point you can go before falling off of somethinga verge or brink.
- Real-life example: The edges of an object are its outermost borders or margins. When you write too close to the edge of a piece of paper, you might write on whatevers next to it, like the surface of the table its on. The edge of a road is the point where it stops and something else begins, such as grass or a sidewalk. The edge of a cliff is the last point you can stand on before there is no more cliff and you will fall. This sense of the word can also be used in figurative ways, as in the edge of reality.
- Used in a sentence:The pencil rolled over the edge of the desk and fell on the floor.
Don’t Miss: What Does Consistent Mean In Algebra
How Do Vertices Faces And Edges Relate To Other Areas Of Maths
Students will use the knowledge of vertices, faces and edges when looking at 2d shapes as well as 3d shapes. Knowing what edges are and identifying them on compound shapes is crucial for finding the perimeter and area of 2d compound shapes. It is an important foundation for later years when dealing with different maths theorems, such as graph theory and parabolas.
Heres A List Of Shapes Along With The Number Of Vertices
|
3D Shape Vertices |
-
An edge in a shape can be defined as a point where two faces meet.
-
For example, a tetrahedron has 4 edges and a pentagon has 5 edges.
-
The line segments that form the skeleton of the 3D shapes are known as edges.
-
For a polygon, we can say that an edge is a line segment on the boundary joining one vertex to another.
-
A Tetrahedron Has 6 Edges
-
For polyhedron shapes a line segment where two faces meet is known as an edge.
You May Like: Geometry Dash Toe 2
Number Of Edges In A Polyhedron
Any convex polyhedron‘s surface has Euler characteristic
- V ,
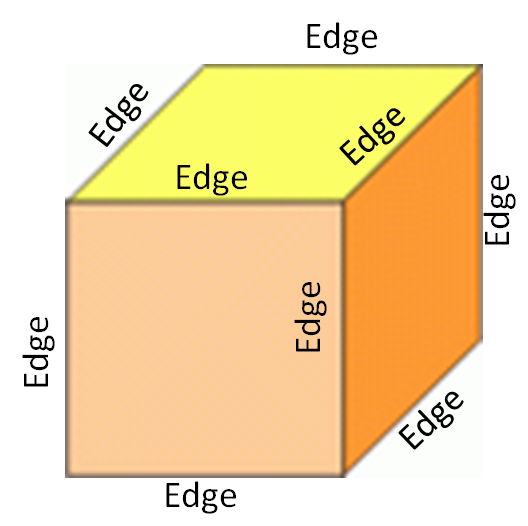
where V is the number of vertices, E is the number of edges, and F is the number of faces. This equation is known as Euler’s polyhedron formula. Thus the number of edges is 2 less than the sum of the numbers of vertices and faces. For example, a cube has 8 vertices and 6 faces, and hence 12 edges.
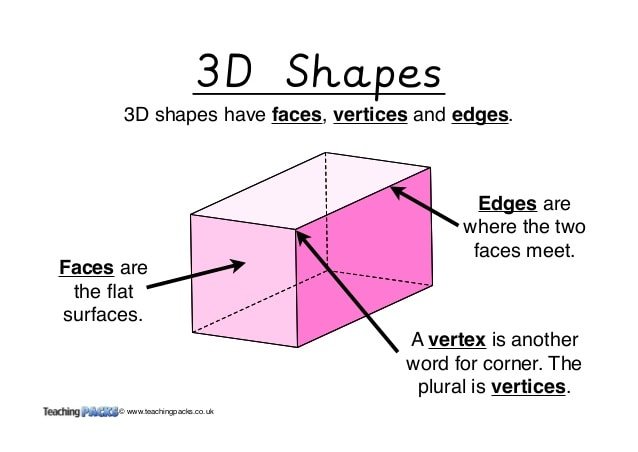
What Are Vertices In Shapes
Vertices in shapes are the points where two or more line segments or edges meet . The singular of vertices is vertex. For example a cube has 8 vertices and a cone has one vertex.Vertices are sometimes called corners but when dealing with 2D and 3D shapes, the word vertices is preferred.
A cube has 8 vertices. 7 are visible here and one is hidden.
Don’t Miss: Algebra 1 Chapter 4 Practice Workbook Answers
The Edges Geometry In Threejs
The edges geometry constructor in three.js is yet another useful little feature of threejs that can be a handy tool when I just want to view the edges of a geometry. I became aware of how this constructor can be useful when I took a second look into how to o about working with wire frames when updating my post on that subject in three.js. When it comes to wire frame mode that works more or less as expected, however it will work by showing all the triangles of a geometry, not just the edges of a geometry as a line, or collection of line segments. So when it comes to creating another kind of wire frame mode that is just the edges of a geometry this constructor can help with that when used with the line constructor. However I think that this constructor deserves a quick post on its own, so here it is.
What Are Vertices Faces And Edges Explained For Primary School
Neil Almond
Vertices, faces and edges come up a lot in primary school geometry when children are learning about the properties of 3d shapes. Here we explain what each of these mean and how to work out the number of vertices, faces and edges for any shape. We also include the number of edges, faces and vertices of the most common shapes.
This vocabulary is introduced in the national curriculum at Year 2, and so the following information can be used with pupils throughout primary school years. Even Year 1 pupils can begin to engage with properties of shapes in this way if you want to give them a head start!
Recommended Reading: Beth Thomas Psychopath
Preview Microsoft Math Solver In Microsoft Edge
For many students, math can be a particularly challenging subject in school. Math is sequential, in that each lesson is part of the foundation for future learning. If students do not have a solid understanding of each concept as they go, it may impact their ability to build the skills necessary to understand more complex and abstract mathematical concepts in the future.
The impact of Covid-19 has forced students to use more digital learning tools and incorporate their web browser into everyday learning. Students rely on the browser to help them find solutions to their studies, including math. To help these students on their learning journey, we are excited to announce that Microsoft Math Solver will be available as a preview feature starting with Microsoft Edge 91 stable.
Microsoft Math Solver allows a student to snap a picture of a math problem be it handwritten or printed and get an instant solution with step-by-step instructions to help them learn how to reach the solution on their own. It includes a mathematical keyboard so students can easily type math problems instead of hunting around a traditional keyboard for the characters they need. It also provides many options to continue learning with additional materials such as quizzes, worksheets, and video tutorials to help students continue to practice and grow their math skills.
Relation To Edges In Graphs
In graph theory, an edge is an abstract object connecting two graph vertices, unlike polygon and polyhedron edges which have a concrete geometric representation as a line segment.However, any polyhedron can be represented by its skeleton or edge-skeleton, a graph whose vertices are the geometric vertices of the polyhedron and whose edges correspond to the geometric edges. Conversely, the graphs that are skeletons of three-dimensional polyhedra can be characterized by Steinitz’s theorem as being exactly the 3-vertex-connectedplanar graphs.
Read Also: Infinite Algebra 1 Properties Of Exponents
How Do Vertices Faces And Edges Relate To Real Life
Any object in real life has vertices, faces and edges. For example, a crystal is an octahedron it has eight faces, twelve edges and six vertices. Knowing these properties for different three-dimensional shapes lays the foundation for various industries such as architecture, interior design, engineering and more.
Vertices Faces And Edges
What is an Edge, Vertex and a Face?
-
A vertex in a geometrical figure can be defined as a corner.
-
A line segment between faces is known as an edge.
-
A single flat surface is known as face.
What are Vertices?
-
A point where two or more line segments meet is known as a vertex.
-
The plural of vertex is vertices.
-
In simpler words, we can say that a vertex is a corner.
-
For example, a tetrahedron has 4 vertices and a pentagon has 5 vertices.
Don’t Miss: Massachusetts Bay Colony Geography And Climate
Incidences With Other Faces
In a polygon, two edges meet at each vertex more generally, by Balinski’s theorem, at least d edges meet at every vertex of a d-dimensional convex polytope.Similarly, in a polyhedron, exactly two two-dimensional faces meet at every edge, while in higher dimensional polytopes three or more two-dimensional faces meet at every edge.
How To Find Non Manifold Areas In A Mesh
While in Edit mode, you can select all non manifold areas with CTRL
One type of non manifold situation is when you have overlapping edges.
For example, I’d frequently have a mesh that’d look fine, like this:
But then when I checked for non manifolds, I would get an edge highlighted like this:
I discovered the reason this edge was highlighted was because there were overlapping edges.The way to find the overlapping edges is to grab one of the middle vertices in the highlighted area , drag it around and see if you discover a hidden edge, like the white one here:
Once you find that edge, delete it, then put the dragged vertex back into place. One trick I discovered about how to put the vertex back into place easily is when you are first dragging it out out of place, only drag it on one axis, rather than freely in 3, because then you only have to snap it back to that one axis, rather than 3.
Read Also: Beth Thomas Father Jailed
Learn About Vertices Edges And Faces
Have you ever tried to make gift boxes or party hats? They’re all 3D shapes made up of vertices, edges and faces!
Vertices are the pointy bits or the corners where edges meet.
Edges are the lines around a shape.
Faces are the sides that you touch when you hold a shape.
Take a look at this gift box:
It’s made up of 6 square faces.
If you fold the faces and glue them together, it becomes a cube with 8 vertices and 12 edges!
Here’s a rectangular shaped gift box:
It’s made up of 6 rectangular faces.
When you join the sides together, it becomes a rectangular prism with 8 vertices and 12 edges!
Here’s a triangular shaped gift box:
It’s made up of 5 faces .
When you join the sides together, it becomes a triangular prism with 6 vertices and 9 edges!
Here’s another triangular gift box:
It’s made up of 5 faces .
When you join the faces together, it becomes a square based pyramid with 5 vertices and 8 edges!
Here’s a round gift box:
It has 2 circular faces and 1 surface.
The surface doesn’t count as a face. Faces are flat.
When you wrap the surface around the circles, it becomes a cylinder with 2 edges and 0 vertices.
There are no sharp, pointy bits in a cylinder!
You can put lots of things inside these different shaped gift boxes!
What about cones?
Take a look at this party hat:
It’s made up of 1 surface and 1 circular face.
When you wrap the surface around the circle it becomes a cone with 1 vertex and 1 edge.
Vertices Faces And Edges Example Questions
1. Explain what a vertex is.
2.How many edges does a triangular prism have?
3.How many vertices does a cone have?
4. How many faces does a cuboid have? What are the 2D shapes of those faces?
5. For all the common prisms add the faces and vertices together and subtract the edges. What do you notice about the answers?
Wondering about how toexplain other key maths vocabulary to your children? Check out our Primary Maths Dictionary, or try these:
You can find plenty of geometry lesson plans and printable worksheets for primary school pupils on theThird Space Learning Maths Hub.
Online 1-to-1 maths lessons trusted by schools and teachersEvery week Third Space Learnings maths specialist tutors support thousands of primary school children with weekly online 1-to-1 lessons and maths interventions. Since 2013 weve helped over 100,000 children become more confident, able mathematicians. Learn more or request a personalised quote to speak to us about your needs and how we can help.
Our online tuition for maths programme provides every child with their own professional one to one maths tutor
Tags
You May Like: Is Paris Michael Jackson Biological Child
What Is Edge In Triangle
Edges are the lines that join to form vertices. A square has four edges and four vertices. A triangle has three of both. A square pyramid, a three-dimensional shape, has different numbers of edges and vertices. It has five vertices, or corners, but it has eight edges to join these vertices together.
Edge Geometry On Medieval Swords
03 Aug, 2020
A swords edge is the whole point of its being. Sorry, we couldn’t resist the pun, and it’s the truth. The entire design of the sword blade, shape, dynamics, hilt form, and construction are all about creating a tool to deliver the edge and point of a sword to its target. In this post we lay out a few ways of considering the most desirable edge geometry for your sword. Given the increase in practice cutting with European swords, we thought the topic would be of interest.
The edge of the sword is where the two planes of the blade meet. This can be a variety of shapes and angles depending on the intended use of the sword and the skill of the person who last worked on honing the edge. Most Medieval and Renaissance European swords are double edged and more or less laterally symmetrical. In this type of sword the planes that diverge from the thickest portion of the blade and taper down to the edge may be called the primary bevel. This bevel may begin at the central ridge of the sword, as in the diamond section blade below, or it may begin to the outside of a fuller or fullers, which is most easily seen in the narrow fuller example. This initial reduction in blade thickness as it approaches the edge is one of the primary factors that can influence a blades cutting ability as well as its durability.
Primary and secondary bevel on a Swedish EKA knife
Craig Johnson
Recommended Reading: Algebra 1 Age Word Problems