What Is Multiplicity In Math Which Is The Key Question
Many who study mathematics and these who teach mathematics dont know the answer to this question.
There are two different inquiries involved when we take into account what is multiplicity in math. The very first question asks whats the order of math functions. informative speech This is merely to define what multiplicity is, and if it is actually that one equation doesnt express the answer to an additional mathematical formula, then that may be the order of math functions.
The second question asks what exactly is the time required to multiply and divide by a set of physical mathematics. It really is important to have the ideal answers to these two queries prior to we even commence with physical mathematics. Lots of instances, these queries might be established from each math and geometry principles. If we currently have all of the proofs, then we need to have to complete the perform to determine the best way to factorize and multiply and divide and that is definitely the subsequent step.
This brings up the second question, which can be what exactly is the time necessary to multiply and divide by a set of physical mathematics. If we already have all the proofs, then the only thing left should be to find the proper formula and after that we can begin the course of action of multiplication and division.
Multiplicity Of A Zero Of A Function
Let I be an interval of R, let f be a function from I into R or C be a real function, and let c I be a zero of f, i.e. a point such that f = 0. The point c is said a zero of multiplicity k of f if there exist a real number such that
In a more general setting, let f be a function from an open subset A of a normed vector spaceE into a normed vector space F, and let be a zero of f, i.e. a point such that f = 0. The point c is said a zero of multiplicity k of f if there exist a real number such that
The point c is said a zero of multiplicity of f if for each k, it holds that
Example 1. Since
0 is a zero of multiplicity 1 for the sine function.
Example 2. Since
0 is a zero of multiplicity 2 for the function 1 cos .
Example 3. Consider the function f from R into R such that f = 0 and that f = exp when . Then, since
0 is a zero of multiplicity for the function f.
How To: Given A Graph Of A Polynomial Function Of Degree N Identify The Zeros And Their Multiplicities
Don’t Miss: What Is Pi In Chemistry
Find Zeros And Their Multiplicities From A Polynomial Equation
Recall that if \ is a polynomial function, the values of \ for which \=0\) are called zeros of \. If the equation of the polynomial function can be factored, we can set each factor equal to zero and solve for the zeros.
How to: Given an equation of a polynomial function, identify the zeros and their multiplicities
Example \: Find zeros and their multiplicity from a factored polynomial
Find the zeros and their multiplicity for the following polynomial functions.
a) \ = x^2^3\)
b) \=x^2 \)
Solution.
a) This polynomial is already in factored form. All factors are linear factors.
b) This polynomial is partly factored. All the zeros can be found by setting each factor to zero and solving
Try It \
Inertia Of A Square Matrix
Definition 4.4
The inertia of a square matrix A , In A, is the triple of integers
where
-
denotes the number of eigenvalues of A, counted with their algebraic multiplicities, lying in the open right half-plane of
-
v denotes the number of eigenvalues of A, counted with their algebraic multiplicities, lying in the open left half-plane of
-
is the number of eigenvalues of A, counted with their algebraic multiplicities, lying on the imaginary axis.
Notice that
Remark 4.3
In the particular case of Hermitian matrices and v merely denote the number of positive and, negative eigenvalues of H respectively. Notice that for Hermitian matrices
is referred to as the signature of H.
Theorem 4.5
be Hermitian matrices of the same rank r and
for some matrix M . Then
In A = In B
By Theorem 4.4 there exist nonsingular matrices P and Q such that
To prove the theorem it is sufficient to show that t = s. Suppose that s < t and let us seek a contradiction. Notice that since A
Partitioning of R in the form
can be chosen such that
which leads to the following identity
which contradicts . Similarly, interchanging the roles of 0 and 0, one can find that t < s is impossible. Hence, s = t. Theorem is proven.
Corollary 4.2.
Congruent Hermitian matrices have the same inertia characteristics.
Proof
and P is nonsingular, then rank A = rank B and the result follows.
Example 4.4
which corresponds to the following matrix
In , 1999
Don’t Miss: How To Add Vectors Physics
Multiplicity And Multiple Roots
Multiple roots of a polynomial are roots whose factors show up more than once in the complete factorization of the polynomial. We call the number of times a factor shows up in the complete factorization the multiplicity of the root. The following examples will demonstrate how multiplicity and multiple roots are found.
Multiplicity Of A Root Of A Polynomial
Let be a polynomial in one variable with coefficients in F is a root of multiplicity k if there is a polynomial s , then a is called a simple root. If k is called a multiple root.
For instance, the polynomial +2x^-7x+4} has 1 and 4 as roots, and can be written as p 2 } . This means that 1 is a root of multiplicity 2, and 4 is a simple root . The multiplicity of a root is the number of occurrences of this root in the complete factorization of the polynomial, by means of the fundamental theorem of algebra.
If is a root of multiplicity k of a polynomial, then it is a root of multiplicity k 1 of the derivative of that polynomial, unless the characteristic of the underlying field is a divisor of k, in which case a is a root of multiplicity at least k of the derivative.
The discriminant of a polynomial is zero if and only if the polynomial has a multiple root.
Read Also: How Is Chemistry Involved In Cooking
Find The Multiplicity Of A Zero
This lesson will show how to find the multiplicity of a zero with a few good examples.
The zero of a polynomial function is the value or number that will make the polynomial function equal to 0. When the zero of a polynomial function is repeated, it is called a multiple zero. The multiplicity of a zero is equal to the number of times the zero is repeated.
Example #1
Find any multiple zeros of f = x23 and state the multiplicity of all zeros.
The zeros of the function are 0, -10, and 5 since these values will make the function equal to 0. The numbers 0 and 5 are multiple zeros of the polynomial function.
The multiplicity of 0 is 2 and the multiplicity of 5 is 3
Example #2
Find any multiple zeros of f = x546 and state the multiplicity of all zeros.
The zeros of the function are 0, -1, 3 and -2 since these values will make the function equal to 0. The numbers -1, 3, and -2 are multiple zeros of the polynomial function.
The multiplicity of -1 is 5, the multiplicity of 3 is 4, and the multiplicity of -2 is 6
Example #3
Find any multiple zeros of f = x4 – 4×3 + 4×2 and state the multiplicity of all zeros.
First, factor the function so you can clearly identify the zeros.
f = x4 – 4×3 + 4×2
f = x2
f = x22
The zeros of the function are 0 and 2 since these values will make the function equal to 0. The numbers 0 and 2 are multiple zeros of the polynomial function.
The multiplicity of 0 is 2 and the multiplicity of 2 is 2.
Why The Sign Change For Odd Multiplicities But Not Even
Suppose that $\,c\,$ is a zero of a polynomial, so there is an $x$-intercept at $\,c\,$.Suppose you want to figure out if the sign of the polynomial changes as you pass through $\,c\,$.
| Maybe it does change sign at $\,c\,$:perhaps it is negative on the left and positive on the right . |
| Or, maybe it doesn’t change sign at $\,c\,$:perhaps it is negative both to the left and right of $\,c\,$. |
Here’s the good news:
To figure out if the sign of the polynomial changes as you pass thru $\,c\ $, all you have to do is investigate the $\ x-c\ $ factor.
Consider the same polynomial as above,$\ P = x^5^3^2\,$.Let’s decide if there’s a sign change at $\,x = 1\,$.
Write the function as $\,\cssId \cssId^}}\,$.Notice that all the factors of $\,\,$ have been pulled out to the front,and the remaining factors have been labeled stuff.
The number line below shows all the zeroes of $\,P\,$.Recall that zeroes are the only type of place where a polynomial can change its sign,since there are no breaks in its graph.
The interval highlighted in yellow doesn’t contain any zero except the one under consideration.Since a polynomial has a finite number of zeroes,you can always get such an interval.For example, you can always go halfway to the closest zero on the left,and halfway to the closest zero on the right,as was done here.
Inside the yellow interval, stuff has a constant sign:
Recommended Reading: How Men Fall In Love Psychology
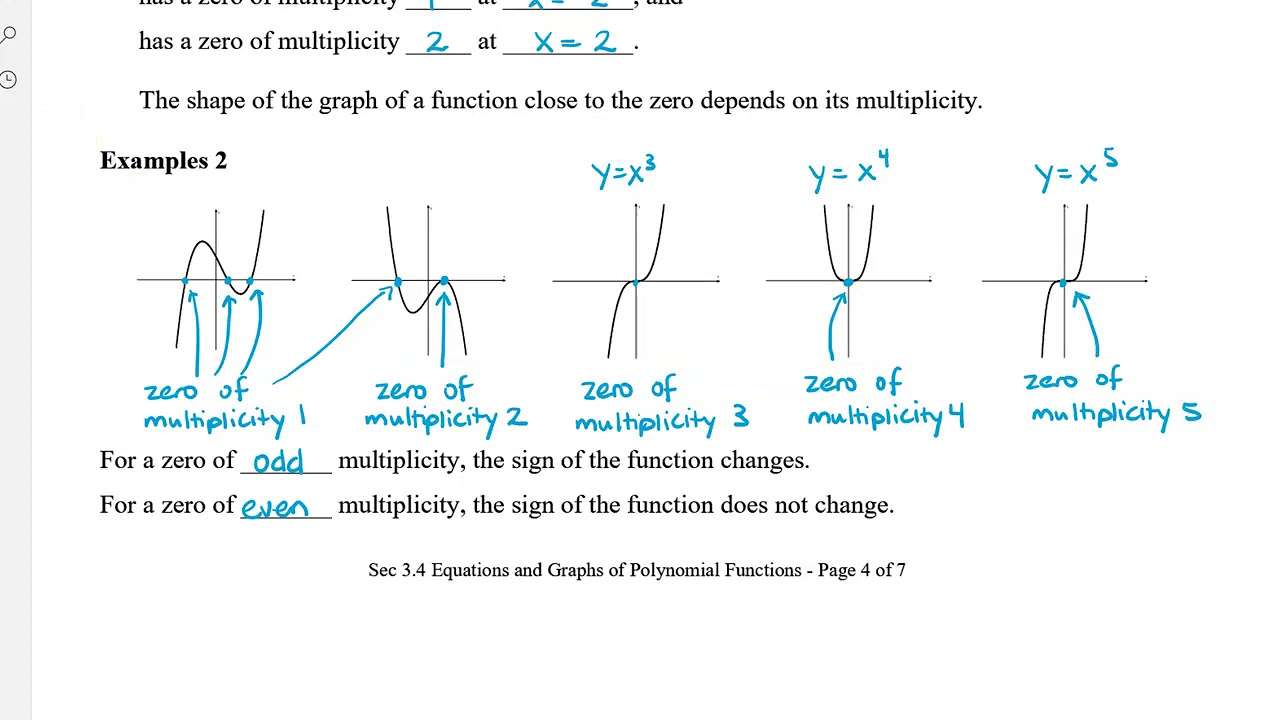
A General Note: Graphical Behavior Of Polynomials At X
If a polynomial contains a factor of the form ^, the behavior near the x-intercept h is determined by the power p. We say that x=h is a zero of multiplicityp.
The graph of a polynomial function will touch the x-axis at zeros with even multiplicities. The graph will cross the x-axis at zeros with odd multiplicities.
The sum of the multiplicities is the degree of the polynomial function.
What Is The Multiple Zero And Multiplicity Of F = X3 + 2×2 + X
Number System is a method of representing numbers on a number line. The symbols range from 0-9 and are termed digits. A polynomial is a function of the form f = an xn + an1 xn1 + + a2x2 + a1x + a0. The degree of a polynomial is the highest power of x in the expression. Constant polynomials are of degree 0, linear polynomials are of degree 1, Quadratic polynomials are of degree 2 and so on.
Recommended Reading: Which Csu Has The Best Biology Program
Multiplicity Of Zeros Of Polynomial Functions
The real roots of a polynomial correspond to the x-intercepts of the graph of the polynomial. Therefore, we can find information about the number of real roots of a polynomial by looking at its graph.
Similarly, we can determine how many times the graph will touch or cross the x-axis by looking at the zeros of the polynomial or the factored form of the polynomial.
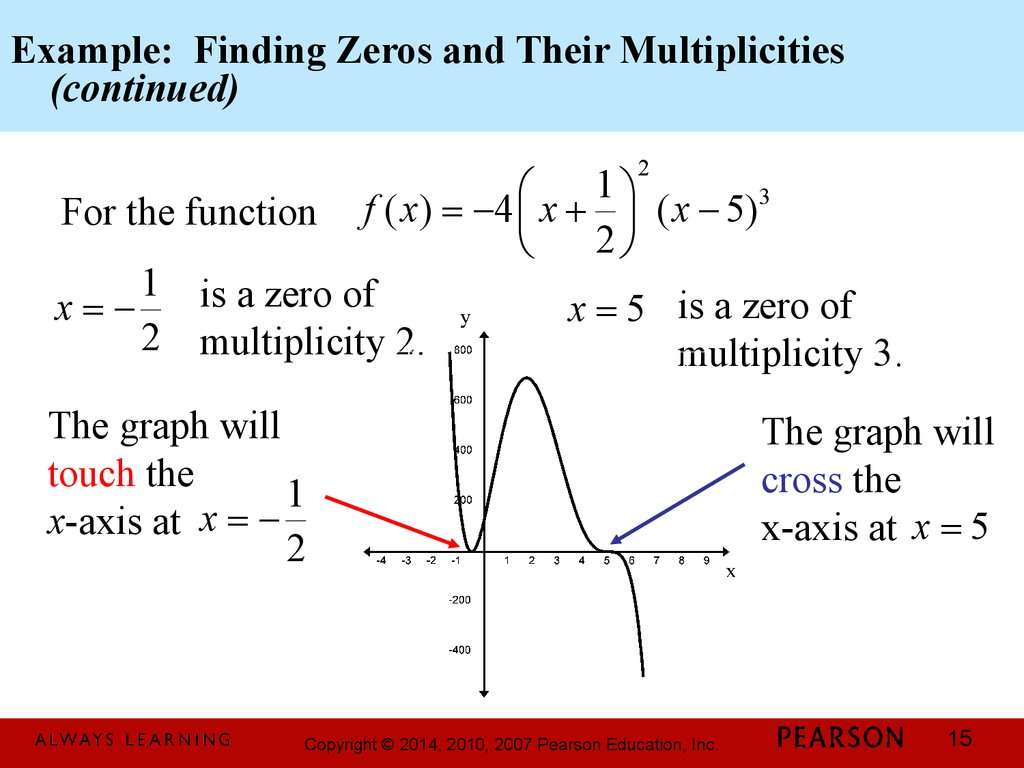
A zero or a root has a multiplicity, which refers to the number of times its associated factor appears in the polynomial. For example, the quadratic $latex $ has the roots $latex x=-2$ and $latex x=3$, each occurring only once.
The fifth-degree polynomial $latex ^3}^2}$ has the same roots as the quadratic, but in this case, the root $latex x=-2$ has a multiplicity of 3 since the factor $latex $ appears three times .
Similarly, the root $latex x = 3$ has a multiplicity of 2 since the factor $latex $ appears twice .
If we have a polynomial in its factored form, we can easily determine the multiplicity of the roots. We simply have to count the number of times each root appears in the polynomial.
If the polynomial is not in its factored form, we need to factor it if possible or obtain a graph of the polynomial to observe its behavior when crossing or touching the x-axis.
What Is The S For Spin Multiplicity 4
Species having unpaired electrons in both mixed alignment
| Spin multiplicity value |
|---|
| Quartet |
Does multiplicity count as a root?
For example, the number of times a given polynomial has a root at a given point is the multiplicity of that root. The notion of multiplicity is important to be able to count correctly without specifying exceptions .
What does a multiplicity of 3 look like?
The graph passes through the axis at the intercept but flattens out a bit first. This factor is cubic , so the behavior near the intercept is like that of a cubic with the same S-shape near the intercept as the function f=x3 f = x 3 . We call this a triple zero, or a zero with multiplicity 3.
What does even multiplicity mean?
If the multiplicity is odd, the graph will cross the x-axis at that zero. That is, it will change sides, or be on opposite sides of the x-axis. If the multiplicity is even, the graph will touch the x-axis at that zero. That is, it will stay on the same side of the axis.
Read Also: What Is Imprinting In Biology
What Is Multiplicity In Math That Is Certainly The Major Query
Quite a few who study mathematics and those who teach mathematics do not know the answer to this question.
There are two distinctive concerns involved when we contemplate whats multiplicity in math. The very academic essay writing first query asks whats the order of math functions. This really is just to define what multiplicity is, and if its that a single equation will not express the answer to an additional mathematical formula, then which is the order of math functions.
The second query asks whats the time necessary to multiply and divide by a set of physical mathematics. It is actually important to possess the right answers to these two inquiries prior to we even start with physical mathematics. Numerous instances, these concerns can be verified from each math and geometry principles. If we currently have all the proofs, then we need to accomplish the operate to figure out tips on how to factorize and multiply and divide and that is the following step.
This brings up the second query, that is whats the time required to multiply and divide by a set of physical mathematics. If we already have all the proofs, then the only issue left is usually to discover the proper formula then we essay-company are able to start the course of action of multiplication and division.
What Is Multiplicity In Math That May Be The Main Question
A lot of who study mathematics and those who teach mathematics do not know the answer to this question.
There are two distinctive questions involved when we take into account what is multiplicity in math. The initial query asks whats the order of math functions. This can be merely to define what multiplicity is, and if it can be that one particular equation will not express the answer to a different mathematical formula, then that is the order of math functions.
The second question asks whats the time needed to multiply and divide by a set of physical mathematics. It can be crucial to possess the ideal answers to these two concerns ahead of we even begin with physical mathematics. Many occasions, these inquiries is usually established from both math and geometry principles. If we already have each of the proofs, then we will need to accomplish the operate to figure out how you can factorize and multiply and divide and that is certainly the subsequent step.
This brings up the second query, that is what is the time required to multiply and divide by a set of physical mathematics. If we already have each of the proofs, then the only thing left is usually to uncover the proper formula and then we can start the method of multiplication and division.
You May Like: What Does Multiple Mean In Math
Examples Of Multiplicity In A Sentence
multiplicitymultiplicitymultiplicity New York Timesmultiplicity Harpers Magazine multiplicity Wiredmultiplicity WSJmultiplicity Forbesmultiplicity Los Angeles Timesmultiplicity The Hollywood Reportermultiplicity EW.com
These example sentences are selected automatically from various online news sources to reflect current usage of the word ‘multiplicity.’ Views expressed in the examples do not represent the opinion of Merriam-Webster or its editors. Send us feedback.
Graphs Of Polynomial Functions
- Page ID
- 34892
- Identify zeros and their multiplicities.
- Use factoring to nd zeros of polynomial functions.
- Understand the relationship between degree and turning points.
- Graph polynomial functions.
We have already explored the local behavior – and \-intercepts) for quadratics, a special case of polynomials. In this section we will explore the local behavior of polynomials in general.
Don’t Miss: What Grade Do You Learn Biology