Combining Powers And Roots
The unit fraction notation used for roots previously may have given you the idea that roots are really the same as powers, only with a unit fraction instead of an integer as the exponent. Thus, the fractional notation is actually preferred in higher mathematics, although the root symbol is still used occasionally, especially for square roots.
Difference Between Power And Exponent With Example
Lets list down the difference between exponent and power with example.
Definition:
In mathematical relationships, power is referred to the number of times a number is multiplied by itself meaning the number you get raising a number to an exponent whereas an exponent can be defined as the number of times the number is used in a multiplication.
Exponents are often known as powers or indices. In simple terms, power can be defined as an expression that represents repeated multiplication of the same number whereas exponent is the quantity that represents the power to which the number is raised. Both these terms are often used interchangeably in mathematical operations.
Example of Power and Exponent:
The expression 5 × 5 × 5 can always be written in a shorter way as 53 using the concept of exponents, 5 × 5 × 5 = 53.The expression basically represents repeated multiplication of the same number which is known as power. Here the number 5 represents the base and the number 3 represents the exponent and the whole expression denotes that 5 to the power of 3 or 5 to the third power which means that over here 5 is multiplied by itself three times.
Similarly, 25 = 2 × 2 × 2 × 2 × 2 is equal to 32.The expression basically denotes 2 to the power of 5 or 2 to the 5th power. In Mathematics, exponents make it easy to write and use multiplications factor.
How To Input Power Symbols
Choose your system to find out.
CharMap allows you to view and use all characters and symbols available in all fonts installed on your computer. You can input power signs using it.
Emoji on iOS
Character Palette
Character Palette allows you to view and use all characters and symbols, including power signs, available in all fonts installed on your computer.
Recommended Reading: How To Find Ksp Chemistry
Example: 24 = 2 2 2 2 = 16
- In words: 24 could be called “2 to the fourth power” or “2 to the power 4” or simply “2 to the 4th”
Exponents make it easier to write and use many multiplications
Example: 96 is easier to write and read than 9 × 9 × 9 × 9 × 9 × 9
You can multiply any number by itself as many times as you want using exponents.
Try here:
| an tells you to multiply a by itself,so there are n of those a‘s: |
Rules For Multiplying Exponents With Square Root

Now, let us use the exponent rules of multiplication that are applicable to expressions in which the bases are square roots.
When the square root bases are the same, the powers are added.
Example: Find the product of 2 and 7.
Solution: The square root bases are the same. Thus, 2× 7 = 2+7 = 9 = 9/2.
When the square root bases are different and the powers are the same, the bases are multiplied first.
Example: Multiply 3× 3
Solution: The square root bases are different and the powers are the same. Thus, 3 and 3= 3 = 3= 3 = 3/2
When the square root bases and the powers are different, the exponents are evaluated separately and then multiplied.
Example: Consider the product of 3 and 4.
Solution: The square root bases and the powers are different. Thus, 3×4= 11.18 × 49 547.82
You May Like: What Happened To Beth Thomas Biological Father
How To Add Exponents
To add exponents, both the exponents and variables should be alike. You add the coefficients of the variables leaving the exponents unchanged. Only terms that have same variables and powers are added. This rule agrees with the multiplication and division of exponents as well.
Below are the steps for adding exponents:
- Check the terms if they have the same bases and exponents
For example, 42+42, these terms have both the same base 4 and exponent 2.
- Compute each term separately if they either have a different base or exponent
For example, 32 + 43, these terms have both different exponents and bases.
- Add the results together.
Power Of Maths Of Powers
Exponentiation is a mathematical operation, written as b, involving two numbers, the base b and the exponent n. When n is a positive integer, exponentiation corresponds to repeated multiplication in other words, is product of a number b multiplied by itself n times.
The exponent is usually shown as a superscript to the right of the base. The exponentiation b can be read as: b raised to the n-th power, b raised to the power of n, or b raised by the exponent of n, most briefly as b to the n. Some exponents have their own pronunciation: for example, b² is usually read as b squared and b³ as b cubed.
The power b can be defined also when n is a negative integer, for nonzero b. No natural extension to all real b and n exists, but when the base b is a positive real number, b can be defined for all real and even complex exponents n via the exponential function ex.
Also this index symbols are used in chemistry to denote chemical elements .
Recommended Reading: Ccl4 Bond Angles
Summary Of Index Laws
`a^mxxa^n = a^`
`a^m/a^n = a^, `
`^n = a^`
`^n = a^nb^n`
`^n = a^n/b^n`
`a^0=1,`
`^n = a^nb^n,`
NOTE 1: These rules apply when a and b are positive and m and n are integers. As a counter-example for the third rule `^n = a^`, if `a< 0` and `n` is a fraction, we could have:
`^` means do `^2 = 9` first, then find square root: `9^ = 3`.
However,
`^` means do ` = 1` first, then raise “ to the power `1`: `^1 = -3`.
The final answers are different, so `^ ^`.
NOTE 2: We don’t have any similar formulas for expressions like `a^m+a^n = …`
This is because we can only add or subtract like terms . For example, this is okay:
`5a^2 + 3a^2 = 8a^2`,
because we are adding like terms.
But we cannot do anything with the following expression:
`5a^3 + 3a^7`
because these are unlike terms .
To see how all this is used in algebra, go to:
Also, this one is often found in mathematics:
`sqrt=a`
This confuses a lot of students. But it just means:
For example, start with 3.
Square it, you get 9.
Take the square root, you get 3, which is back where you started.
Why does it matter? Often we need to “undo” a square when solving an equation, so we find the square root of bothsides. Its good to know what you are doing.
Exponent Tables And Patterns
There are many interesting patterns to be found in the tables of powers of whole numbers.
| Powers of |
| 1048576 |
One thing you may notice are the patterns in the one’s digits. In the powers of 2 table, the ones digits form the repeating pattern 2 table, the ones digits form the repeating pattern 3 . We leave it to you to figure out why this happens!
In the powers of table, the ones digits alternate: 4 . In fact, you can see that the powers of 4 are the same as the even powers of 2
The same relationship exists between the powers of 3
zeros after it. For 10 . The powers of 10 are widely used in , so it’s a good idea to get comfortable with them.
| Powers of |
is a nice pattern between the negative powers of 2
Recommended Reading: Correlational Research Design Psychology
What Is Multiplying Exponents
Before exploring the concept of multiplying exponents, let us recall the meaning of exponents. An exponent can be defined as the number of times a quantity is multiplied by itself. For example, when 2 is multiplied thrice by itself, it is expressed as 2 × 2 × 2 = 23. Here, 2 is the base, and 3 is the power or exponent. It is read as “2 raised to the power of 3”.
Now, let us discuss what multiplying exponents mean. When any two expressions with exponents are multiplied, it is called multiplying exponents. Let us go through the different cases with the help of examples to understand the concept better.
Understanding Powers Of A Power In Algebra
- Inside the brackets is a power, x2. It consists of a base raised to an exponent .x2 means x is multiplied by itself 2 times:x2 = x × x
- This power becomes the base of another power, 3. Here, the base is x2 and the exponent is 3.3 means x2 is multiplied by itself 3 times:3 = x2× x2× x2By writing out this in full, we see that the left hand side is equal to x multiplied by itself 6 times: x6.x2× x2× x2 = × × x2× x2× x2 = x × x × x × x × x × xx2× x2× x2 = x6
- x2 × 3 is a power. It consists of a base raised to an exponent .Clearly, x2 × 3 is equal to x6. The left hand side of the equation equals the right hand side.
Don’t Miss: What Does Abiotic Mean In Biology
Rules For Multiplying Exponents With The Same Base
Consider two expressions with the same base, that is, an and am. Here, the base is ‘a’. When the terms with the same base are multiplied, the powers are added, i.e., am× an = a
Let us explore some examples to understand how the powers are added.
Example 1: Multiply 24× 22
Solution: Here, the base is the same, that is, 2. According to the rule, we will add the powers, 24× 22 = 2 = 26 = 64.
Let us verify the answer. 24× 22 = × = 2 × 2 × 2 × 2 × 2 × 2 = 26 = 64
Example 2: Find the product of 1045 and 1039
Solution: In the given question, the base is the same, that is, 10. According to the rule, we will add the powers, 1045× 1039 = 10 = 1084.
Will the rule still remain the same if the bases are different? Let us see this in the following section.
Calculating The Power Of A Number In Java Without Using Math Pow Method
We need to calculate a number raised to the power of some other number without using the predefined function java.lang.Math.pow
In Java, we can calculate the power of any number by :
Attention reader! Dont stop learning now. Get hold of all the important Java Foundation and Collections concepts with the Fundamentals of Java and Java Collections Course at a student-friendly price and become industry ready. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.
To calculate the power of any number, the base number and an exponent are required.
Prerequisite:
The basic understanding of Java arithmetic operators, data types, basic input/output and loop etc.
Example:
Input : base = 3, exponent = 3Output: 27Input : base = 2, exponent = 4Output: 16
Implementation:
1. Using while loop: The base and power values have been assigned respective values. Now, the while Loop will keep multiplying result variable by base variable until the power becomes zero.
Below is the implementation of the problem statement using the while loop:
You May Like: What Does Relationship Mean In Math Terms
We Will Discuss Exponent Vs Power
Powers and exponents are tools to rewrite long multiplication problems easily in mathematics, especially in algebra. Algebra is known to be one of the key branches of mathematics which deals primarily with the concept of number theory. It can also be referred to as the study of mathematical symbols. You might have noticed superscript in mathematical relationships superscripts can be defined as the one that is placed above to the right of a number. This is known as an exponent and the whole expression can be called as exponentiation.
The operation involves two numbers that can be written in this way xa, where x is equal to the base number and a can be defined as the exponent. The exponent can be basically known as a superscript that is used to simplify larger mathematical problems. The whole expression is known as power and written as x to the power of a where a is any positive integer.
Multiplying And Dividing With Powers
In the same way, 42× 43 = 42+3 = 45 = 1024.Compare 42 = 16, 43 = 64, 16 × 64 = 1024.
It has to be the same number we raise to each power.We cannot multiply 42× 33 in this way.
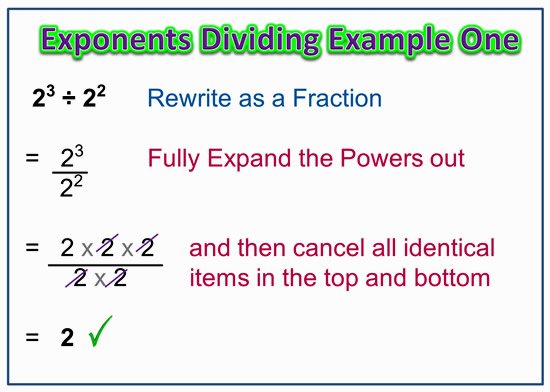
If we divide two numbers both raised to powers, we subtract the powers.For example, 32 / 31 = 9/3 = 3.If we divide 32 / 31 we get / 3 = 3.We can also subtract the second power from the first: 32 / 31 = 321 = 31 = 3.
Recommended Reading: Geometry Holt Mcdougal Answers
How To Do Powers In Math
Solving powers requires an understanding of multiplication rules. A power, or exponent, is a shortcut to indicate a number should be multiplied by itself. The number being multiplied is referred to as the “base.” The exponent is located to the right of the base in superscript or with the ^ symbol appearing before it.
Determine if the base is negative or positive.
Check for parenthesis placement, especially when working with a negative base. Keep in mind ^4 is different from -3^4.
For a positive base, multiply the number as indicated by the exponent. For 5^3, multiple 5_5_5 to arrive at your answer of 125.
For a base whose negative sign is contained in the parenthesis, keep the negative symbol in front of each act of multiplication. For example, ^4 would be multiplied as *, to arrive at your answer of 81.
For exponents whose negative sign is without parenthesis, save the negative symbol until after you have finished multiplying the base. For example, -3^4 would be multiplied as -, to arrive at your answer of -81.
If you have an equation consisting of two exponents with the same base, you can add the exponents together for simplification. For example, 2^3_2_4 can be converted to 2^7. Then, you can solve the equation as usual.
Tips
Multiplying Numbers With The Same Base
We often need to multiply something like the following:
43× 45
We note the numbers have the same base and we think of it as follows:
43× 45 ` = \underbrace_ xx \underbrace_`
We get 3 fours from the first bracket and 5 fours from the second bracket, so altogether we will have 3 + 5 = 8 fours multiplied together.
43× 45 = 43+5 = 48
In general, we can say for any number a and indices m and n:
am×an = a
Recommended Reading: Who Are Paris Jackson’s Biological Parents
The Interesting World Of Mathematics Power Calculator
Mathematics power, or simply exponent, is the method of multiplying a number by itself. The number in the exponential portion is the number of times you’ll need to multiply the number. The mathematics power calculator is a simple maths calculator that tells you how much a number equals in its exponential form. We are talking about squares, cubes and higher exponential powers here.
For example: if you are asked to find out the square of 5, 5², you’ll simply need to multiply 5 by itself:
Similarly, the cube of 5 will be:
These numbers may look easy to calculate, some numbers really are. Like the square of 15 , or square of 25 , or cube of 4 , or 34 .
But as the numbers go higher and the exponential power increases, finding the right answer starts becoming more and more difficult.
This is where a mathematics power calculator comes into the picture. But before we talk about this math calculator in detail let’s take a look at the exponential function in detail.
What Is Power In Mathematics
Power can be defined as a mathematical expression that can be used to represent exactly how many times a number should be used in a multiplication process. In simple words, it is an expression that describes repeated multiplication of the same given number. Power in mathematics is written as raising a number to the power of any other number.
Lets consider the following example:
3 × 3 × 3 × 3 this is equal to 81. This can also be written in this manner 34 = 81. This is an exponential notation and it simply means the number the number 3 is to be multiplied four times by itself to get the number 81 or in other words we can say 3 raised to the power of 4 or 3 raised to the 4th power gives us 81. The number 3 is known as the base number and 4 is known as the power or exponent.
Also Check: Ccl4 Lewis Structure Shape
Negative And Noninteger Powers
A base may also be raised to a negative, fractional, or decimal power. These will be covered later in this lesson
5 }=25^=5}
Note, however, that most square roots don’t yield integers, and many don’t even produce rational numbers.
Manually finding a square root
One method for manually taking square roots is to repeatedly do long division. Let’s take the square root of 10 in this example. We would start by estimating the answer. Since 32 = 9 and 42 = 16, we know the answer lies between 3 and 4. Furthermore, since 10 is only one away from 9, but is 6 away from 16, we could estimate that the answer is one-seventh of the way between 3 and 4. This won’t give an exact answer, and a seventh is ugly to work with, so let’s use a fifth, instead. This gives us 3 1/5 or 3.2 as a starting estimate.
Now do long division to divide 10 by 3.2. We get 3.125. The average of 3.2 and 3.125 is /2 = 6.325/2 = 3.1625, so that will be our next estimate.
Now do long division to divide 10 by 3.1625. We get 3.162055… . The average of 3.1625 and 3.1621 is 3.1623, so that will be our next estimate.
Now do long division to divide 10 by 3.1623. We get 3.162255…
So, this method can be repeated to get the desired level of accuracy. The actual square root of 10 is 3.16227766…
Note that calculators or computers are used for most square root calculations, but knowing how to manually calculate a square root can be quite useful when no calculator is available.