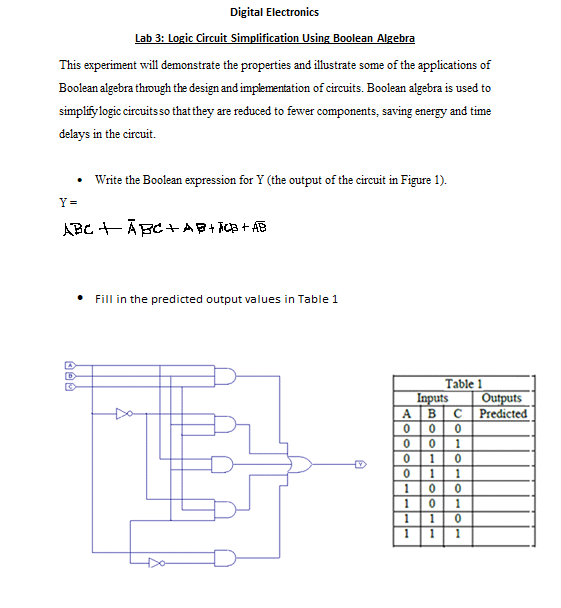
Circuit Simplification Using Boolean Algebra
The algebraic method used to simplify digital circuits applies a number of Boolean laws to successively simplify complex equations. Selected laws and rules are applied, step by step, to the original equation, so as to eventually arrive at a simplified version that can be implemented with a smaller number of gates and therefore lead to a simpler circuit.
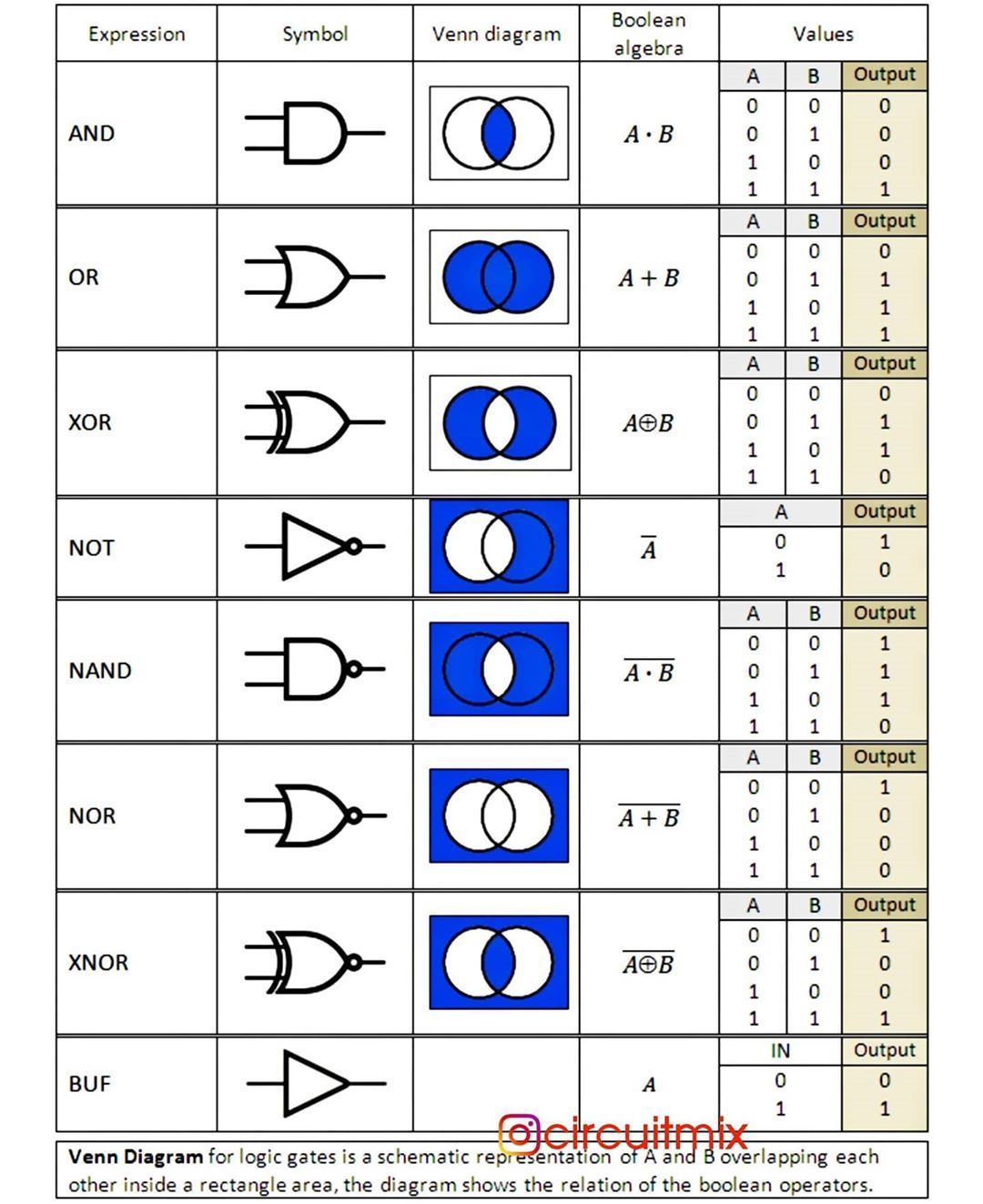
Logic Gates And Truth Tables
Logic circuit truth tables show the status of the output terminal or terminals of logic gates and logic circuits for all the possible input combinations. The gate or circuit’s input states are shown in the left columns of the table while the corresponding output states are shown in the right columns.
The tables opposite show the range of common logic gates with their corresponding truth tables.
Digital Logic Boolean Algebra
I am having a hard time understanding why A’+B’ is not equal to the following expression:
I understand that when I apply the 4 different combinations: 00,01,10,11 to A and B I get different results for reach expression when we have either the combination 01 or 10.
Is that the only explanation? For some reason I always figured the two expressions would yield the same results.
Try writing it out:
_ _ _ _ _____A B | A B A + B A + B A + B-----+----------------+-----------------0 0 | 1 1 1 | 0 11 0 | 0 1 1 | 1 00 1 | 1 0 1 | 1 01 1 | 0 0 0 | 1 0
\$ \bar A + \bar B \$ is true if either A is false OR B is false.
\$ \overline \$ is true if both A and B are false.
Read Also: What Is Paramagnetic And Diamagnetic In Chemistry
History Of Boolean Algebra
As mentioned earlier, Boolean algebra is invented in the year of 1854, by an English mathematician George Boole. He first stated the idea of the Boolean algebra in his book An Investigation of the Laws of Thought.
After this, the Boolean algebra is well known as the perfect way for representing the digital logic circuits.
In the late 19th century, scientists Jevons, Schroder and Huntington used this concept for modernized concepts. And in the year of 1936, M.H.Stone proved that the Boolean algebra is isomorphic to the sets .
In 1930s , a scientist named, Claude Shannon developed a new type algebra method as Switching Algebra by using the Boolean algebra concepts, for studying the switching circuits.
The logic synthesis of the modern electronic automation tools is efficiently represented by using Boolean functions known as Binary Decision Diagrams.
Boolean algebra allows only two states of a logic circuit, as True and False or High and Low or Yes and No or Open and Close or 0 and 1.
Boolean Expressions
These are similar to that of the mathematical expression. The Boolean expressions are formed by combining the logical variables by using the logical operators. For example
S Used In Duality Theorem

Here are some of the main steps used to solve duality theorem in boolean algebra:
- Change each AND operation to an OR operation
- Change each OR operation to an AND operation
- Complement each 1 and 0
Let’s take an example to apply all the above three steps to understand about duality principle in a practical way. This example gives you some idea about how to convert or apply duality theorem or principle in any boolean expression.
1+0 = 1
The dual of the above statement will be:
0.1 = 0
As you can see here, we have done the following:
- changed first 1 to 0
- changed OR to AND
- changed first 0 to 1
- changed second 1 to 0
Read Also: What Is Banking In Physics
Fig 234 Nand Only Cash Room Access Circuit
A better option could be to replace the AND and OR functions with universal gates such as NOR or NAND. A NAND only version of the simplified circuit is shown in Fig. 2.3.4. This version uses three gates instead of two, but all the gates are the same and can be accommodated within a single 7400 IC. The original circuit has therefore now been reduced from four ICs to one.
Boolean Algebra Has Three Basic Operations
OR: Also known as Disjunction. This operation is performed on two Boolean variables. The output of the OR operation will be 0 when both of the operands are 0, otherwise it will be 1.
To get a clearer picture of what this operation does we can visualize it with the help of a Truth Table below.
Truth tables give us an insightful representation of what the Boolean operations do and they also act as a handy tool for performing Boolean operations.OR OperationVariable-1Variable-2Output 000 011 101 111
AND: Also known as Conjunction. This operation is performed on two Boolean variables. The output of AND operations will be 1 when both operands are 1, otherwise it will be 0. The truth table representation is as follows.
AND OperationVariable-1Variable-2Output 000 010 100 111
NOT: Also known as Negation. This operation is performed only on one variable. If the value of the variable is 1 then this operation simply converts it into 0 and if the value of the variable is 0, then it converts it into 1.
Not OperationVariable-1Output 01 10
Don’t Miss: What Is Velocity In Physics
The Transistor As A Switch
Electronic gates are generally constructed from transistor circuits which depend for their operation on the use of the transistor as a switch, rather than as an amplifier for which it was originally invented. With no voltage on the base, there is no current through the transistor which is thus switched off and the output voltage will be high. When a “high” voltage is applied to the base the transistor is switched on and output voltage will be “low”. See more on the page about semiconductors.
|
An early version of a bi-stable switching circuit was the 1919 Eccles and Jordan flip-flop based on valves . The later transistor version was one of the first electronic circuits to be implemented as an Integrated Circuit by Robert Noyce in 1959. Flip-flops rely on the concept of feedback in which the output of a circuit is fed back into the input such that when the input is high, the output is low and vice versa. See below an example of transistor switches used in the electronic circuit used to implement a three input NOR gate |
How Is Boolean Algebra Used In Digital Electronics
Boolean algebra has been fundamental in the development of digital electronics, and is provided for in all modern programming languages. It is also used in set theory and statistics. A precursor of Boolean algebra was Gottfried Wilhelm Leibniz s algebra of concepts.
What are the roles of addition and multiplication in Boolean algebra?
Addition and multiplication then play the Boolean roles of XOR and AND , respectively, with disjunction x y definable as x + y xy . Boolean algebra also deals with functions which have their values in the set .
Read Also: What Are Stressors In Psychology
Rules In Boolean Algebra
Addition Rule In Boolean Algebra
The table given below shows the addition rule used in boolean algebra:
| Input 1 |
|---|
Or you can also write the addition rule without table, as given below:
0+0=00+1=11+0=11+1=1
It works same as OR gate works. That is, if any one from all the input is 1, then the output will be 1, otherwise the output will be 0.
Don’t Miss: 10 Algebra Questions And Answers
Duality Principle Of Boolean Algebra
Duality principle is an important property used mainly in proving various theorems availablein boolean algebra.
Duality principle states that in a two-valued boolean algebra, the dual of an algebraic expression can be obtained by interchanging all the OR and AND operator and by replacing 1 by 0 and 0 by 1.
Laws Of Boolean Algebra Faqs
Q.1 What are the three primary operators of Boolean algebra?Ans.1 Q.2 What are the various boolean algebra laws?Ans.2 Q.3 What are some of the boolean algebra theorems?Ans.3 Q.4 How can we define a boolean function?Ans.4 Q.5 What does boolean algebra imply?Ans.5 Q.6 How do we define literals?Ans.6 Q.7 What does complement mean?Ans.7
Also Check: Who Is Considered The Founder Of Psychology
Application Of Logic Gates
Logic gates are used to implement the following digital circuit.
Bank Alarm System
A bank wants to install an alarm system with 3 movement sensors.
To prevent false alarms produced by a single sensor activation, the alarm will be triggered only when at least two sensors activate simultaneously.
Other logic applications like Odd numbers, Multiplexers, Adders, BCD to 7 segment decoder …which you learn how to use logic gates to implement in minutes!
With advertising revenues falling despite increasing numbers of visitors, we need your help to maintain and improve this site, which takes time, money and hard work. Thanks to the generosity of our visitors who gave earlier, you are able to use this site at no charge.
If you have benefited from this site and are able, pleasegive $10 via Paypal. It will allow uscontinue into the future. It only takes a minute. Thanks!
A Digital Circuit And How To Make It
What youll learn
Logic Gates And Boolean Algebra in Digital Electronics
- In this course, you will learn about logic gates and the different types of logic gates that they belong to.
- Here, you will learn about each logic gate and how it works, as well as the internal circuit structures for each gate.
- It doesnt end there. Youll also learn how to solve any logical circuit questions and how to reduce or simplify a given boolean algebraic expression, too.
Requirements
- Everything you need to know will be learned. There is no need to know anything before you start.
Description
Its important to watch the videos in high-resolution mode to get a better look.
When it comes to Logic Gates
All of us know how digital computers, communication systems, digital display units, the internet, emails, and so on have changed our lives. The digital computers, communication systems, digital display units, the internet, and emails that we use every day all work on the principle of digital techniques.
There are many logic gates that you will learn about in this class. These are the building blocks or units of digital systems.
If you want to be a computer science engineer or a student of electronics, you can take this class! Below are the things that are in the logic gates session.
Youll also learn about positive logic representation and negative logic representation, which are two types of logic.
Boolean Algebra is a type of math.
Who this course is for:
Read Also: Geometry Dash The Secret Box
Basic Operations And Logic Gates
These axioms are the principles of the operations. We will see the three basic operations that are the AND, OR and NOT operations. For that we will use two Boolean variables a and b that can assume 0 and 1, or false and true.
For the construction of digital systems we use logic gates. There are three basic logic gates and others are formed with a combination of them. These gates can be realized in the real world with electronic circuits with transistors or FETs.
Minimization Of Boolean Expression
Boolean functions can be reduced to as simple a form as possible before the actual realization. The realization of digital circuits with minimal expression has several benefits like the number of logical gate requirements will be reduced as a result the speed of operation will be enhanced. This would also reduce the complexity of the circuit and hence power dissipation will be reduced.
A boolean function can be reduced by using certain algebraic rules and theorems as mentioned above which results in the reduction of the number of terms or the arithmetic operations.
Also, check out the other topics of Digital Electronics, here.
We hope that the above article on the Laws of Boolean Algebra is helpful for your understanding and exam preparations. Stay tuned to the Testbook app for more updates on related topics from Digital Electronics, and various such subjects. Also, reach out to the test series available to examine your knowledge regarding several exams.
You May Like: What Does The Word Biology Mean
Fig 232 Cash Room Access Circuit
This suggests a circuit like that shown in Fig. 2.3.2, which would require four I.Cs:
1x 74HCT08 2 input AND .
1x 74HCT10 3 input AND .
1x 74HCT32 2 input OR .
1x 74HCT4075 3 input OR .
However, by choosing appropriate laws and rules from those listed above, the circuit can be considerably simplified.
Starting with the equation derived from Table 2.3.4:
The Prototypical Boolean Algebra
The set and its Boolean operations as treated above can be understood as the special case of bit vectors of length one, which by the identification of bit vectors with subsets can also be understood as the two subsets of a one-element set. We call this the prototypical Boolean algebra, justified by the following observation.
- The laws satisfied by all nondegenerate concrete Boolean algebras coincide with those satisfied by the prototypical Boolean algebra.
This observation is easily proved as follows. Certainly any law satisfied by all concrete Boolean algebras is satisfied by the prototypical one since it is concrete. Conversely any law that fails for some concrete Boolean algebra must have failed at a particular bit position, in which case that position by itself furnishes a one-bit counterexample to that law. Nondegeneracy ensures the existence of at least one bit position because there is only one empty bit vector.
The final goal of the next section can be understood as eliminating “concrete” from the above observation. We shall however reach that goal via the surprisingly stronger observation that, up to isomorphism, all Boolean algebras are concrete.
Also Check: Where’s My Water Cool Math Games
Diving Deeper Into Boolean Algebra
This has been a pretty lightweight article that has hopefully prepared you for a number of articles that will explore many aspects of digital logic and Boolean Algebra at a much deeper level — in fact at a level deeper than most courses go. This is useful because to truly master digital logic design, and it is necessary to be fully conversant with the concepts and subtleties upon which it is based and to also be aware of the common misconceptions and fallacies that frequently trap less well-prepared designers.
Interested in learning more about Boolean algebra? Read on in the next article in the series: Boolean Identities
Application Of Boolean Algebra
Combinational Logic Circuit Design comprises the following steps
With advertising revenues falling despite increasing numbers of visitors, we need your help to maintain and improve this site, which takes time, money and hard work. Thanks to the generosity of our visitors who gave earlier, you are able to use this site at no charge.
If you have benefited from this site and are able, pleasegive $10 via Paypal. It will allow uscontinue into the future. It only takes a minute. Thanks!
You May Like: What Is Reductionism In Psychology
Why Is An Understanding Of Boolean Algebra Important To Computer Scientists
Answer: Boolean Algebra is important to computer science majors because it teaches the basic designs for the circuits used in digital computers.
What is Boolean Algebra What was its original purpose?
Boolean algebra is a division of mathematics that deals with operations on logical values and incorporates binary variables. Boolean algebra traces its origins to an 1854 book by mathematician George Boole. The distinguishing factor of Boolean algebra is that it deals only with the study of binary variables.
Boolean Logic And Digital Circuits
Modern digital computers are built from digital logic circuits whose basic building blocks are logic gates, each of which is designed to implement a specific logical function. Information is held in data “words”, representing data or instructions, made up from strings of individual “bits” with binary values of 1 or 0. These values are analogous to Boolean logic propositions and the statements or conclusions derived from them which were defined as “true” or “false”. Boolean algebra is the tool used to design combinations of gates to implement more complex functions such as mathematical operations, control functions and data storage.
Recommended Reading: What Does Equivalent Mean In Math
Applying De Morgans Theorem
These equalities, generally called De Morgans Laws 1 and 2 are illustrated in Fig. 2.3.5 and Fig. 2.3.6 as they apply to AND, NOR, NAND and OR gates. Note however, that when De Morgans theorem is applied to the XOR and XNOR gates there is no change in the gates function.
The usefulness of De Morgans theorem when applied to circuits can be seen by comparing Fig. 2.3.3 and Fig. 2.3.4 where it was instrumental in changing the functions of the AND and OR gates in Fig.2.3.3 to all NAND gates in Fig. 2.3.4, so the circuit can be made using one IC instead of two.
Why Is Boolean Algebra So Important In Digital Systems
Today, Boolean algebra is of significance to the theory of probability, geometry of sets, and information theory. Furthermore, it constitutes the basis for the design of circuits used in electronic digital computers.
Why is Boolean logic so important today?
Equally important, Boolean logic is today seen as the foundations of the information age, or what we also call the computer age. This is because each value in these logical statements or equations reduces down to either being true or false, with zero ambiguity. The logic is binary.
Also Check: Formulas To Remember For Geometry