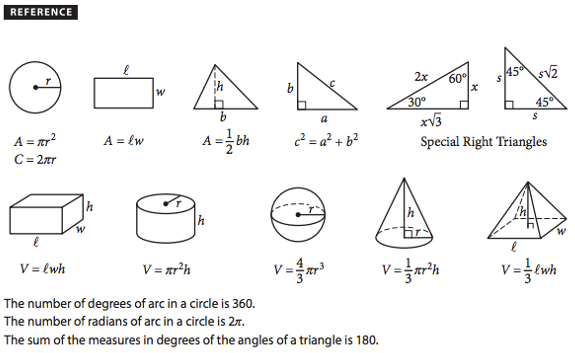
Area And Circumference Of Circle
“Around the circle” is the circumference. Circumference = × d .
Area Of A Circle Apple pies are square: A = × r2Apple pies are round: A = × r × r
Circumference Of A Circle Cherry pie’s delicious!: Circumference = × d Apple pies are too!: Area = × r2
Isosceles Triangle Sing this to the tune of “Oh Christmas Tree”: Oh isosceles, oh isosceles
A sentence to help you spell isoscelesI sat on sunny cliff eating lovely egg sandwiches
Do You Know How To Improve Your Profile For College Applications
See how your profile ranks among thousands of other students using CollegeVine. Calculate your chances at your dream schools and learn what areas you need to improve right now it only takes 3 minutes and it’s 100% free.
In theory, the ACT Math Test seems fairly straightforward: 60 questions in 60 minutes, calculator permitted. Every question is multiple-choice, and theres also no guessing penalty, which means that wrong answers wont deduct any points from your total score. For more information on scoring specifics, check out the Complete Guide to Your ACT Score Report.
Topics covered on ACT Math include middle and high school algebra, plane and coordinate geometry, statistics and probability, and trigonometry. Unlike on the SAT, however, the ACT doesnt provide a formula sheet/box for reference during the test. As such, its crucial that you memorize the formulas youll need and practice using them ahead of test day. In this post, well discuss why the ACT matters and which formulas are important for success on ACT Math.
Sector Area In A Circle
Similar to arc length, this formula provides the area of the sector between two given radii intersecting at the circle center with central angle . The \ incorporates circle area into this formula.
Percentages are used to express parts of a whole, and the \ symbol generally means divide by 100. As such, the above equation answers any problem asking for \ of quantity \.
Read Also: Why Are There Different Branches Of Chemistry
Igcse Maths Formula Sheet / Mathematics 0580 Formula Sheet
Geometry math circle theorems gcse formulas maths revision igcse circles mathematics cheat calculus science equations notes biology teaching grade . Designed by the expert teachers at save my exams. Students are not expected to memorise complicated formulae but may need to remember simple . It includes all the formulas. There is no formulae sheet provided with mathematics examinations.
Formulas Not Given On The Test
For most of the formulas on this list, you’ll simply need to buckle down and memorize them . Some of them, however, can be useful to know but are ultimately unnecessary to memorize, as their results can be calculated via other means. .
We’ve broken the list into “Need to Know” and “Good to Know,” depending on if you are a formula-loving test taker or a fewer-formulas-the-better kind of test taker.
You May Like: What Is The Molecular Geometry Of Ccl4
Properties Of Special Right Triangle: Isosceles Triangle
- An isosceles triangle has two sides that are equal in length and two equal angles opposite those sides.
- An isosceles right triangle always has a 90-degree angle and two 45 degree angles.
- The side lengths are determined by the formula: $x$, $x$, $x2$, with the hypotenuse having a length of one of the smaller sides *$2$.
- E.g., An isosceles right triangle may have side lengths of $12$, $12$, and $122$.
Binomial Product 1difference Of Squares
\=x^2-y^2\)
The best times to recognize the binomial products and quickly factor them is on the no-calculator section. You dont have to FOIL or use any other methodyou can quickly convert from the factored form to the expanded form on sight. The difference of squares is used often by SAT test makers in a variety of contexts.
Recommended Reading: Exponential Growth And Decay Common Core Algebra 1 Homework Answers
Linear Equations & Functions
There will be at least five to six questions on linear equations and functions on every ACT test, so this is a very important section to know.
Slope
Slope is the measure of how a line changes. Its expressed as: the change along the y-axis/the change along the x-axis, or $\rise/\run$.
- Given two points, $A$, $B$, find the slope of the line that connects them:
$$/$$
Slope-Intercept Form
- A linear equation is written as $y=mx+b$
- m is the slope and b is the y-intercept
- A line that passes through the origin , is written as $y=mx$
- If you get an equation that is NOT written this way , re-write it into $y=mx+b$
- Given two points, $A$, $B$, find the midpoint of the line that connects them:
$$/2, /2)$$
- Find the distance between the two points
$$$$
- You dont actually need this formula, as you can simply graph your points and then create a right triangle from them. The distance will be the hypotenuse, which you can find via the pythagorean theorem
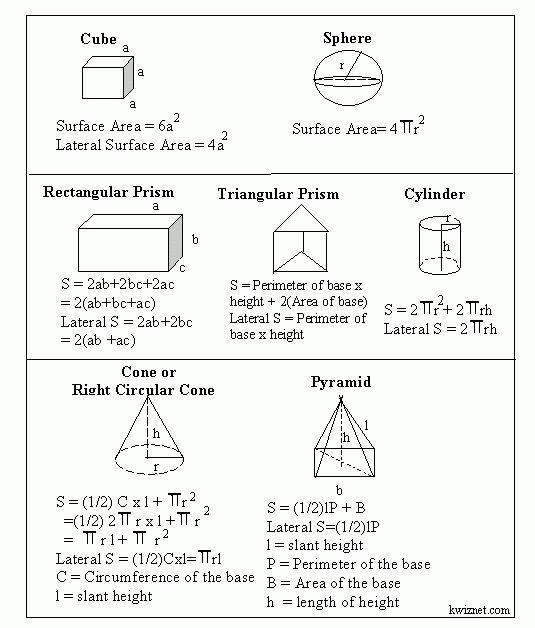
Topic : Volume And Surface Area
These SAT geometry questions are likely to test any of the following:
- The volume of regular solids
- The surface area of regular solids
In general, theres not too much to memorize with volume and surface area for the SAT.
The reference information at the beginning of each section of SAT math will provide most of the necessary formulas, and any uncommon formulas will most likely be given in the problem.
But remember: you can save valuable time by memorizing the formulas provided in the reference information!
Volume
Its helpful to remember that the volume of all regular solids can be found using the following formula:
- Volume = Area of base x Height
Most volume questions on the SAT involve right cylinders. Since the base of a cylinder is a circle, these questions will also incorporate concepts involving circles .
Below are the volume formulas that you should know for the test:
- Volume of a Cylinder
Lets look at an example of a question involving volume:
How to solve:
If the volume of the cylinder is equal to 72 and the height is 8 yards, then plugging into the formula for the volume of a right cylinder, we get 72=8r^2. Solving for r, that gets us 3 yards.
However, the question is asking about diameter, not radius. Since diameter=2r, the answer is 6 yards.
Some volume problems might be more involved, combining multiple shapes into a single question. Lets look at one of those:
How to solve:
Surface Area
For most prisms, this is pretty straightforward.
You May Like: How To Study For Ap Human Geography
What Is A Math Formula And Why Is It Important
In mathematics, a formula is a word equation that defines how to find the unknown variables within the equation in terms of other known values. It is commonly used to describe data that is being graphed or plotted.
Mathematical formulas are important because they help us visualize data and get a better understanding of the concept. They can also be used as a step-by-step guide to solving problems in different areas.
There are many different types of mathematical equations. The most common ones are linear, exponential, logarithmic, and trigonometric equations.
Quick Formula Reference Sheet
And dont forget to download the quick formula reference sheet. Keep this sheet around for a quick reminder when you forget one of the formulas. Press the button below to download this PDF.
Best of luck,
Dr. SteveGet 800
p.s.: Dont forget to take a look at the following special offer on all of my SAT math prep books: SAT Math Prep Books Full Bundle
Also Check: Who Are Paris Jackson’s Biological Parents
Solved Examples Using Geometry Formulas
Example 1: Calculate the circumference and the area and of a circle by using geometry formulas if the radius of the circle is 21 units?
Solution:
To find the area and the circumference of the circle:
Given: Radius of a circle = 21 unitsUsing geometry formulas for circle,Area of circle = ×r2 = 3.142857 × 212Now for the circumference of the circle,Using geometry formulas for circle,Circumference of a Circle = 2r= 2= 131.95
Answer: The area of a circle is 1385.44 sq. units and the circumference of a circle is 131.95 units.
Example 2: What is the area of a rectangular park whose length and breadth are 60m and 90m respectively?
Solution:To find the area of a rectangular park:
Given: Length of the park = 60m
The breadth of the park = 90mUsing geometry formulas for rectangle,
Area of Rectangle =
= m2
= 5400 m2
Answer: The area of the rectangular park is 5400 m2.
Example 3: Using geometry formulas of the cube, calculate the surface area and volume of a cube whose edge is 6 units respectively?
Solution:To Find: The surface area and volume of a cube whose edge is 6 units
Using geometry formulas of cube,Surface area of cube is = A = 6a2A = 6 2A = 6 × 36 = 216 units2Volume of a cube, V = a3V = 3V = 216 units3
Answer: The surface area of the cube is 216 units2. The volume of the cube is 216 units3
Geometry Rules: Right Triangles

Any right triangle has two sides touching the right angle: these are called legs. The longest side, always opposite the right angle, is called the hypotenuse.
One geometry rule that applies to all right triangles is theorem named for Mr. Pythagoras , whom some scholars consider the first mathematician.
Notice that the side we call c, the side alone on one side of the equation, has to be the hypotenuse. Also, notice that we can apply this formula unless we know a triangle is a right triangle, and that is not something we can assume simply from looks. If we get the litter perpendicular square, as we have here, then we know its a right triangle and we can apply this geometry equation.
Of course, some or all of the sides of a right triangle can be decimals, but it is possible, in special cases, for all three sides to be integers. These are sets of three integers that satisfy the Pythagorean Theorem. The most common is and its multiples, but other good ones to recognize are , , and .
There are two very special triangles that you have to understand for GRE geometry. The first is the 30-60-90 triangle:
The other triangle is the 45-45-90 triangle, also known as the Isosceles Right Triangle.
Again, the ratios always are the same and we can multiply by any number. The two legs are always equal because this is an isosceles triangle, and the hypotenuse is always the square-root of two times any leg. GRE loves all the geometry formulas associated with these two triangles.
Read Also: How To Find Ksp Chemistry
Sat Math Formulas You Need To Know
Have you ever been stumped on a math test question, only to realize how simple it was when you later reviewed your test? Thats exactly what happens to many students who take the SAT.
The SAT covers a wide range of mathfrom as early as elementary school all the way to senior year of high school. While you probably learned these formulas at some point, it may have been a while since youve had to use them. This is part of what makes the SAT challenging: since it draws on many different types of math, you need to get out of the high school math mindset and review the math youve learned over the years.
If you dont do any studying for the SAT, youll take longer to recall certain helpful formulas and concepts. While theres always more than one way to reach the right answer, being able to quickly remember these math facts will help you answer questions more efficiently and minimize careless mistakes. Weve categorized these formulas to help you focus your preparation, and weve provided a quick review of what each concept is.
Want to know your chances at the schools youre applying for based on your SAT score? Calculate your admissions chances right now.
The Math Formulas You Should Memorize For The Sat
I frequently get asked about the key math formulas that students really need to know for the SAT. After 15 years of tutoring SAT math, I have created a small list of the most important formulas that students should memorize. Everything you need to know on this subject is below.
Important note: The formulas in this post are for the old SAT. If you will be taking the SAT beginning March 2016 you may want to follow the following link: Math Formulas for the Revised SAT
Don’t Miss: Eoc Fsa Warm Ups Algebra 1 Answers
Understand The Underlying Math Concepts
While memorization is a reliable method for getting these GRE math formulas under your belt, you should also try to actively understand the concepts behind them. Knowing what these formulas signify and how theyre connected to other formulas is particularly helpful for those struggling to memorize all of them.
What do I mean by this exactly? Lets look at a couple of examples.
First off, its important to know the definitions of the vocab words used in these formulas. Lets say a question requires you to solve for the perimeter of a rectangle. Even if you cant recall the perimeter formula , start by asking yourself whether you know what a perimeter is or not. Hopefully, you remember a perimeter is the total length around a shape, or the total length of all sides of a shape. In other words, just add up the four sides of a rectangle! By knowing just the definition of the term, you can solve for the perimeter of a rectangle, with or without a formula.
But remembering a definition isnt always enough. Sometimes, you have to look for relationships among formulas in order to understand why they are the way they are.
Heres an example. Look at the area formula for a triangle and compare it to the area formula for a rectangle. For the rectangle, another way of writing the area formula is b multiplied by h . The two formulas look like this:
Triangle: $A=bh$
Rectangle: $A=bh$
Introduction: Connecting Your Learning
Most students in high school and college math ask the question, “When will I ever use this concept in real life?” In reality, geometry has many practical applications to the everyday world as well as the computer world.
Geometry can be interesting when you think about how it is connected to the design of computer applications including real and virtual objects, or if you are trying to determine information about and properties of a geospatial location or area. In this module, you will discuss area of geometric figures and objects. By the end of the module, you should know the meaning and notation for area and the area formulas for some common geometric figures, and be able to calculate the area of some common geometric figures.
Recommended Reading: Unit 1 Test Geometry Basics Answers Key
Properties Of Special Right Triangle: 30 60 90 Degree Triangle
- A 30, 60, 90 triangle describes the degree measures of the triangle’s three angles.
- The side lengths are determined by the formula: $x$, $x3$, and $2x$
- The side opposite 30 degrees is the smallest, with a measurement of $x$.
- The side opposite 60 degrees is the middle length, with a measurement of $x3$.
- The side opposite 90 degree is the hypotenuse , with a length of $2x$.
- For example, a 30-60-90 triangle may have side lengths of $5$, $53$, and $10$.
Organize Your Studying By Grouping Similar Formulas Together
When youre studying for a math test, its easy to feel overwhelmed and miss parts of the formulas youre working on. By organizing your studying by grouping similar formulas together, it can be easier to manage your time and not risk falling behind in the course.
The two main types of formulas that can be organized are arithmetic formulas and geometric formulas.
The first type is typically made up of multiplication, division, addition, subtraction, fractions, and percentage calculations. The second type contains patterns such as arches or spirals that are often seen in nature or when moving through space.
When organizing a study session by grouping similar formulas together such as these two examples above, it makes it possible for students to focus their attention on just one formula at a time in order to study efficiently without getting lost or overwhelmed.
Recommended Reading: Kendall Hunt Geometry Answer Key
Is This All You Need For Gre Math
In a word, no. Although these formulas are helpful and often necessary for doing well on the GRE, familiarizing yourself with this list alone doesnt guarantee you an excellent Quant score.
To perform well on Quant, you must know, in addition to formulas, how to interpret data correctly, how to understand what a question is asking you to solve, and what basic terms like quotient and prime number mean. You should also know how to factor polynomials and how to compare quantities using ratios. These are just a handful of the several areas of math youll be tested on. To learn more about what exactly you should know for Quant, check out our in-depth math review.
As a final word of advice, always remember to use PEMDAS , consult your calculator when necessary, and, above all, practice, practice, practice! Good luck!
Geometry Rules: Angles And Lines
A right angle is made up of 90 degrees. A straight line is made up of 180 degrees.
In this diagram, ADC is a straight line. BTW, make sure you dont confuse straight lines with horizontal lines. Any line that doesnt bend or curve is straight, regardless of direction. By contrast, a horizontal line is parallel to the top or bottom of the page, parallel to the distant horizon. Line ADC is straight but not horizontal.
Notice, also, that straightness is one of the very few things we can assume on the GRE. If it looks like theres no bend in the line, then theres no bend: i.e. if it looks straight, it is straight. By contrast, we cannot assume perpendicularity: if we didnt have that special little blue square guaranteeing that the lines were perpendicular, we could not assume that either angle ADB or angle BCD were right angles. That is something we must be told, in one form or another.
If two lines intersect, the sum of the resulting four angles equals 360°. Furthermore, the angles opposite each other have to be equal. These angles meet at just a vertex, so they are called vertical angles .
When a line intersects a set of parallel lines, we get many more angles. We get eight angles: four big angles and four small angles. There are a number of technical names that we dont have to know for GRE geometry. We just have to know that every big angle is equal, every small angle is equal, and any big angle and any small angle are supplementary.
You May Like: What Is The Molecular Geometry Of Ccl4